Понятие вероятности события

Примеры задач

Пример 1

Найти вероятность того, что наугад вытащенная из колоды карт будет бубновой масти (сумма карт в колоде кратна $4$-м).

Решение.

Так как количество карт кратно четверке, то пусть всего карт будет $4k$. Тогда каждой масти карт будет $k$ штук (так как мастей $4$ и их количество одинаково).

При решении этой задачи будем использовать определение $5$. Во введенных нами обозначениях, получим что в определении $5$ мы будем иметь

$N=4k,n=k$

Следовательно

$P=\frac{k}{4k}=\frac{1}{4}$

Ответ: $\frac{1}{4}$.

Пример 2

Пусть нам дана точка $(a,b)$, где $-5

Решение.

Тут мы будем использовать геометрическое определение. Изобразим вначале область, в которую в принципе может попасть эта точка (рис. 1).

Из этого рисунка видим, что

$S=8\cdot 5=40,s=3\cdot 3=9$

Тогда из геометрического определения:

$P=\frac{9}{40}$
Ответ: $\frac{9}{40}$.

Статистическое определение вероятности

Пусть в некоторой серии из $n$ испытаний случайное событие $A$ происходит $m$ раз. Постоянная величина $P\left(A\right)$, к которой стремится относительная частота $\frac{m}{n} $ при неограниченном увеличении количества испытаний $n$, называется статистической вероятностью события $A$, то есть $P\left(A\right)=\mathop{\lim }\limits_{n\to \infty } \frac{m}{n} $.

Поскольку обеспечить $n\to \infty $ практически нереально, то относительную частоту $\frac{m}{n} $ называют эмпирической оценкой вероятности $P\left(A\right)$ события $A$.

Например, чтобы узнать, какова вероятность изготовления качественного прибора на данном рабочем месте, проверяют определенную партию приборов. Предположим, что при оценке партии из 400 приборов 380 оказались качественными. Относительная частота $\frac{380}{400} =0,95$ является эмпирической оценкой вероятности изготовления качественного прибора на данном рабочем месте.

Классификация событий

Одним из основных понятий теории вероятностей является понятие события.
Подсобытиемпонимают
любой факт, который может произойти в результате опыта или
испытания. Подопытом,
илииспытанием,
понимается осуществление определённого комплекса условий.

Примеры событий:

– попадание в цель при выстреле из орудия (опыт —
произведение выстрела; событие — попадание в цель);
– выпадение двух гербов при трёхкратном бросании монеты (опыт —
трёхкратное бросание монеты; событие — выпадение двух гербов);
– появление ошибки измерения в заданных пределах при измерении
дальности до цели (опыт — измерение дальности; событие — ошибка
измерения).

Можно привести бесчисленное множество подобных примеров.
События обозначаются заглавными буквами латинского алфавитаи
т.д.

Различаютсобытия
совместныеинесовместные.
События называются совместными, если наступление одного из них не
исключает наступления другого. В противном случае события называются
несовместными. Например, подбрасываются две игральные кости. Событие—
выпадание трех очков на первой игральной кости, событие—
выпадание трех очков на второй кости.и—
совместные события. Пусть в магазин поступила партия обуви одного
фасона и размера, но разного цвета. Событие—
наудачу взятая коробка окажется с обувью черного цвета, событие—
коробка окажется с обувью коричневого цвета,и—
несовместные события.

Событие называетсядостоверным,
если оно обязательно произойдет в условиях данного опыта.

Событие называется невозможным, если оно не может произойти в условиях
данного опыта. Например, событие, заключающееся в том, что из партии
стандартных деталей будет взята стандартная деталь, является
достоверным, а нестандартная — невозможным.

Событие называетсявозможным,
илислучайным,
если в результате опыта оно может появиться, но может и не
появиться. Примером случайного события может служить выявление
дефектов изделия при контроле партии готовой продукции,
несоответствие размера обрабатываемого изделия заданному, отказ
одного из звеньев автоматизированной системы управления.

События называютсяравновозможными,
если по условиям испытания ни одно из этих событий не является
объективно более возможным, чем другие. Например, пусть магазину
поставляют электролампочки (причем в равных количествах) несколько
заводов-изготовителей. События, состоящие в покупке лампочки любого
из этих заводов, равновозможны.

Важным понятием являетсяполная
группа событий. Несколько событий в данном опыте образуют
полную группу, если в результате опыта обязательно появится хотя бы
одно из них. Например, в урне находится десять шаров, из них шесть
шаров красных, четыре белых, причем пять шаров имеют номера.—
появление красного шара при одном извлечении,—
появление белого шара,—
появление шара с номером. Событияобразуют
полную группу совместных событий.

Введем понятие противоположного, или дополнительного, события. Подпротивоположнымсобытиемпонимается
событие, которое обязательно должно произойти, если не наступило
некоторое событие.
Противоположные события несовместны и единственно возможны. Они
образуют полную группу событий. Например, если партия изготовленных
изделий состоит из годных и бракованных, то при извлечении одного
изделия оно может оказаться либо годным — событие, либо
бракованным — событие.

8.3. Свойства вероятности

Суммой событий A и B называется событие C = A + B, состоящее
в наступлении, по крайней мере, одного из событий — A или B.

Теорема. Вероятность суммы двух несовместных событий
A и B равна сумме вероятностей этих событий: P (A + B) = P(A) + P(B).

Примеры: пусть А — идет дождь, а В — идет снег, то (А
+ В) — либо дождь, либо снег, либо дождь со снегом, т. е. осадки; А
— пошли на дискотеку; В — пошли в библиотеку, то А + В — пошли либо
на дискотеку, либо в библиотеку, т. е. вышли из дома.

Следствие. Сумма вероятностей противоположных событий А и равна
единице:

Вероятность суммы полной группы событий равна 1.

Примеры: если А — число четное, то — число нечетное;
если А — зима, то — не зима (либо осень, либо лето, либо весна); если
А — сдал экзамен, то — не сдал экзамен.

Произведением событий А и В называется событие С = АВ, состоящее
в том, что в результате испытания произошло и событие А и событие В.

Примеры: пусть А — из урны вытянули белый шар, В — из
урны вытянули белый шар, то АВ — из урны вытянули два белых шара; А
— идет дождь, В — идет снег, то АВ — дождь со снегом; А — число четное,
В — число кратное 3, то АВ — число кратное 6.

Два события A и B называются независимыми, если вероятность появления
каждого из них не зависит от того, появилось другое событие или нет.
В противном случае события A и B называются зависимыми.

Чаще всего зависимые испытания происходят тогда, когда тянут из одной
колоды, не возвращая карты в колоду, вытаскивают из одной урны и т.
д.

Теорема. Вероятность произведения двух независимых событий
A и B равна произведению их вероятностей:

Пусть А и В — зависимые. Условной вероятностью PA (B) события В называется
вероятность события В, найденная в предположении, что событие А уже
наступило.

Теорема. Вероятность произведения двух зависимых событий
A и B равна произведению вероятности одного из них на условную вероятность
другого, найденного в предположении, что первое событие уже наступило:

Теорема. Вероятность суммы двух совместных событий A
и B равна сумме вероятностей этих событий минус вероятность их произведения

Теорема (формула полной вероятности).
Вероятность события A, которое может наступить лишь при условии появления
одного из n попарно несовместных событий B1, B2,…, Bn, образующих полную
группу, равна сумме произведений вероятностей каждого из этих событий
на соответствующую условную вероятность события A:

Теорема (формула Байеса). Если существуют n попарно
несовместных событий B₁, B₂, …, B_n,
образующих полную группу, и известны условные вероятности события А,
то можно найти вероятности того, что событие А произошло при условии
появления некоторого события B_k по формуле:

8.1. Понятие о случайном событии

Наблюдение явления, опыт, эксперимент, которые можно провести многократно,
в теории вероятностей принято называть испытанием. Примеры: сдача
экзамена, наблюдение за дорожно-транспортными происшествиями, выстрел
из винтовки, бросание игрального кубика, педагогический эксперимент.

Результат, исход испытания называется событием. Примеры: успешная
сдача экзамена, дорожно-транспортные происшествия со смертельным исходом,
попадание в цель, появление того или иного числа очков на брошенной
игральной кости, получение результата при проведении педагогического
эксперимента.

Два события называются совместными, если появление одного из
них не исключает появления другого в одном и том же испытании. Примеры:
совместные события: идет дождь и идет снег, человек ест и человек
читает, число целое и четное; несовместные события: день и ночь,
человек читает и человек спит, число иррациональное и четное.

Два события называются противоположными, если в данном испытании
они несовместны и одно из них обязательно происходит. Примеры:
если сейчас день, то сейчас не ночь; если человек спит, то в данный
момент он не читает; если число иррациональное, то оно не является четным.

Событие называется достоверным, если в данном испытании оно
является единственно возможным его исходом. Событие называется невозможным,
если в данном испытании оно заведомо не может произойти. Примеры:
если в урне все шары белые, то достать белый шар является достоверным
событием, а достать черный шар является невозможным событием; если человек
прыгнул в воду, то выйти мокрым является достоверным событием, а выйти
сухим является невозможным событием.

Событие называется случайным, если его наступление или ненаступление
в некотором испытании (эксперименте) зависит от ряда случайных факторов.
Примеры: успешная сдача экзамена; выигрыш в лотерее;
рождения мальчика или девочки; всхожесть семян; попадание в цель и т.
д.

Противоположные события

Заметим, что если сложить вероятности всех элементарных событий, которые возможны в ходе эксперимента, то получится единица. Действительно, при броске монеты возможны два события с вероятностью 1/2. Сумма их вероятностей составляет 1/2 + 1/2 = 1.

Это правило действует и в том случае, когда речь идет о не равновозможных событиях. Так, при выстреле по мишени возможны два варианта развития событий – попадание в цель или промах. Пусть вероятность попадания в цель равна 0,3. Это значит, что вероятность промаха составляет 0,7, так как только в этом случае сумма этих вероятностей будет равна единице:

0,7 + 0,3 = 1

Заметим, что при стрельбе стрелок либо попадет в цель, либо промажет. То есть одно из двух этих событий обязательно произойдет, но только оно одно. Подобные события называют противоположными.

Противоположными являются такие события, как:

• падение монеты либо одной стороной вверх (орлом), либо другой (решкой);
• выпадение четного или нечетного числа на шестигранном кубике;
• изготовление рабочим годной или получение бракованной детали.

Стоит отметить, что победа одной и победа другой команды в футбольном матче – это не противоположные события, так как возможен третий исход – ничья. Однако в ряде спортивных состязаний ничья невозможна, и тогда победы команд – это противоположные события.

Очевидно, что сумма вероятностей противоположных событий равна единице.

Пример. Вероятность того, что рабочий изготовит годную деталь, оценивается в 0,97. Чему равна вероятность изготовления бракованной детали?

Решение. Изготовление бракованной детали (обозначим это событие как А) и получение годного изделие (событие Б) – это два противоположных события. Их сумма равна единице

Р(А) + Р(B) = 1

По условию Р(А) = 0,97. Тогда

0,97 + Р(В) = 1

Перенесем в равенстве слагаемое 0,97 в правую часть и получим:

Р(B) = 1 – 0,97

Р(В) = 0,03

Ответ: 0,03

Статистическое определение вероятности

Рассмотрим статистическое определение вероятности, чтобы понимать статистический подход к численному определению вероятности. Данный подход очень важен тогда, когда из теоретических соображений подобный к соображению симметрии, значение вероятности событий наперёд невозможно установить.

К примеру, если у партии из 100 случайно отобранных для контроля товара, обнаружено 2 нестандартных, тогда утверждение, что соотношение (его называют относительной частотой), можно считать вероятностью появления нестандартного товара, не может быть убедительным. Этот пример в схему случаев не вписывается. Теоретически вероятность такого события установить невозможно. Однако, выход есть, если много раз повторить выборки.(при одинаковых условиях) и проследить за значением относительных частот событий, то есть, воспользоваться статистическими методами.

Определение

Относительной частотой случайного события называется отношение , числа испытаний, в которых это событие появилось, к общему числу , проведённых испытаний, и обозначается:

Между относительной частотой и вероятностью событий есть определённая связь: если каким-то образом установлено, что вероятность случайного события равняется числу , тогда при больших версиях испытаний и неизменных условиях частота события приблизительно равняется вероятности, то есть:

.

Для подтверждения этого равенства подбросим раз монеты. В данном случае “герб” появлялся раз, – относительная частота выпадания “герба”.

Независимые и зависимые события

Прогуляемся в магазин за булочками. В упаковке две булочки, а сама упаковка непрозрачная, то есть увидеть булочки до вскрытия упаковки мы не можем. 

Известно, что на заводе, где изготавливаются булочки, 5 из 100 булочек подгорают. Значит, 95 из 100 булочек не подгорают. По классическому определению вероятности находим, что вероятность каждой булочки не подгореть равна \(\frac{95}{100} = 0,95\). 

Какова вероятность, что в упаковке попадутся только не подгорелые булочки? Как найти вероятность сразу для двух булочек?

Ответим на вопрос: зависят ли булочки друг от друга? 

Если подгорит одна из булочек в упаковке, не обязательно подгорит другая. Следовательно, булочки не зависят друг от друга. Такие события называются независимыми. 

Независимые события — такие события, появление одного из которых не зависит от появления другого события. 

Определим вероятность независимых событий. 

Пусть вероятность, что подгорела первая булочка, будет равна Р(А) = 0,95, а вероятность для второй булочки будет равна Р(В) = 0,95. 

А чтобы найти вероятность независимых событий, нужно воспользоваться следующей формулой:

\(P(A \cap B) = P(A) * P(B)\)

Тогда вероятность, что булочки в одной упаковке не подгорят, равняется P = 0,95 * 0,95 = 0,9025. 

В каком случае нужно пользоваться этой формулой? Нужно подставить союз “и”. 

Мы хотим, чтобы в упаковке первая булочка была не подгорелой и вторая булочка была не подгорелой. 

Приведем еще один пример. В здании два автомата с кофе на разных этажах. Даже если сломается один из них, работа второго не будет зависеть от первого. 

Но если автоматы стоят  рядом и включены в одну розетку, то при поломке одного из них есть вероятность выхода из строя розетки, а значит, и второй автомат тоже сломается. Такие события будут зависимыми: появление одного из них зависит от появления другого. 

Предположим, что в мешке лежит семь кубиков: два из них оранжевые, а пять — фиолетовые. Из мешка дважды вытаскивают кубики. Какова вероятность, достать во второй раз именно фиолетовый кубик?

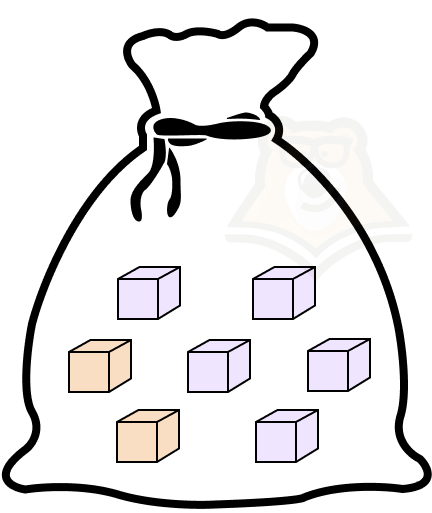
Нужная последовательность может быть в двух случаях:

• сначала вытащат фиолетовый кубик и потом снова фиолетовый;
• сначала вытащат оранжевый кубик, а потом фиолетовый. 

Разберем первый случай. Вероятность в первый раз вытащить фиолетовый кубик равна \(\frac{5}{7}\). После этого в мешке останется шесть кубиков, четыре из которых будут фиолетовые. 

Вероятность вытащить во второй раз фиолетовый кубик равна \(\frac{5}{7} * \frac{4}{6} = \frac{20}{42} = \frac{10}{21}\). 

Теперь рассмотрим второй случай. Вероятность в первый раз достать оранжевый кубик равна \(\frac{2}{7}\). В мешке останется шесть кубиков, пять из которых будут фиолетовыми. 

Вероятность вытащить во второй раз фиолетовый кубик будет уже равна \(\frac{2}{7} * \frac{5}{6} = \frac{10}{42} = \frac{5}{21}\). 

В этом примере очень наглядно видно, что вероятность напрямую зависит от того, какой кубик попался первым. Следовательно, эти события зависимы. 

Как отличить зависимые и независимые события? Если после наступления первого события меняется количество благоприятных и всех исходов, то такие события — зависимые. Если количество благоприятных и всех исходов не меняется, то события независимые.

Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А. 

Условная вероятность обозначается P(B|A). В нашем примере условной вероятностью будет вычисление, что во второй раз попадется именно фиолетовый кубик.   

Найдем вероятность двух зависимых событий. Формула похожа на ту, что используется для независимых событий. Но в этот раз нам нужно применить условную вероятность. 

Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило:\(P(A \cap B) = P(A) * P(B | A)\)

Статистические закономерности

 В литературе по теории вероятностей эксперименты проводились несколькими учёными, о которых остались записи. Давайте их вспомним:

Автор эксперимента
Бюффон (1707-1788) – французский естествоиспытатель, натуралист, биолог, математик	4040	0,507
Де Морган (1806-1871) – шотландский математик, логик	4090	0,5005
Джевонс (1835-1882) – английский экономист и философ	20 480	0,5068
Романовский В. И. (1879-1954) – советский математик	80 640	0,4933
Пирсон К. (1857-1936) – английский математик-статистик, биолог, философ.	24 000	0,5005
Феллер У. (1906-1970) – американский математик.	10 000	0,4979

Вышеперечисленные результаты испытаний (экспериментов) полностью согласовываются с теоретическим значением вероятности, которая равняется 0,5 и получена предположительно равной возможности “герба” и “числа”, то есть симметричной монеты. При помощи специальных вероятных методов за данными испытаниями можно установить, что выпадания “герба” или “числа” в отдельных случаях не одинаково вероятно, то есть монета не симметрична.

Ряд статистических закономерностей были обнаружены в конце XIX и в начале XX столетия в физике, химии, биологии, экономике и других науках. Было установлено, что если опыты проводятся при неизменных условиях, в каждом из которых число испытаний достаточно большое, тогда число испытаний, при которых данное событие появилось, то есть частота событий , как правило, мало отличается от вероятности появления событий . И чем большее количество испытаний, тем реже встречаются частоты , которые значительно отклоняются от вероятности .

Как видите, при многоразовых испытаниях, относительная частота, которая еле меняется, колеблется вокруг некоторого числа, которое есть вероятностью событий. Согласно статистическому определению за вероятность событий принимается относительная частота или число, близкое к ней.

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

2.1. Теорема сложения вероятностей несовместных событий

Суммой  двух
событий  и
 называют
событие, состоящее в появлении события ,
или события ,
или обоих этих событий. Например, если из орудия произведены два выстрела и  —
попадание при первом выстреле,  —
попадание при втором выстреле, то  —
попадание при первом выстреле, или при втором, или в обоих выстрелах.

В частности, если два события  и
 —
несовместные, то  —
событие, состоящее в появлении одного из этих событий, безразлично какого.

Суммой нескольких событий называют событие, которое
состоит в появлении хотя бы одного из этих событий. Например, событие  состоит
в появлении одного из следующих событий: ,
 и
,
 и
,
 и
,
 и
 и
.

Пусть события  и
 —
несовместные, причем вероятности этих событий известны. Как найти вероятность
того, что наступит либо событие ,
либо событие ?
Ответ на этот вопрос дает теорема сложения.

Теорема. Вероятность появления одного из двух
несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Доказательство.
Введем обозначения:  —
общее число возможных элементарных исходов испытания;  —
число исходов, благоприятствующих событию ;
 —
число исходов, благоприятствующих событию .

Число элементарных исходов, благоприятствующих наступлению
либо события ,
либо события ,
равно .
Следовательно,

Приняв во внимание, что  и
,
окончательно получим

Следствие.
Вероятность появления одного из нескольких попарно несовместных событий,
безразлично какого, равна сумме вероятностей этих событий:

Доказательство.
Рассмотрим три события: ,
 и
.
Так как рассматриваемые события попарно несовместны, то появление одного из трех
событий, ,
 и
,
равносильно наступлению одного из двух событий,  и
,
поэтому в силу указанной теоремы

Для произвольного числа попарно несовместных событий
доказательство проводится методом математической индукции.

Пример 2.1. В
урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления
цветного шара.

Решение.
Появление цветного шара означает появление либо красного, либо синего шара.

Вероятность появления красного шара (событие )

Вероятность появления синего шара (событие )

События  и
 несовместны
(появление шара одного цвета исключает появление шара другого цвета), поэтому
теорема сложения применима.

Искомая вероятность

Пример 2.
Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в
первую область равна 0,45, во вторую — 0,35. Найти вероятность того, что стрелок
при одном выстреле попадет либо в первую, либо во вторую область.

Решение. События
 —
«стрелок попал в первую область» и  —
«стрелок попал во вторую область» — несовместны (попадание в одну область
исключает попадание в другую), поэтому теорема сложения применима.

Искомая вероятность

8.2. Определение вероятности

Совокупность образует полную группу событий для данного испытания,
если его результатом обязательно становится хотя бы одно из них. Например,
при сдаче зачета возможны следующие исходы: «зачтено», «не
зачтено», «не явился»; при подбрасывании монеты — «орел»,
«решка»; при подбрасывании игральной кости — 1, 2, 3, 4, 5,
6.

События, образующие полную группу попарно несовместных и равновозможных
событий, будем называть элементарными событиями.

Классическое определение вероятности

Вероятностью P(A) события A называется отношение числа элементарных
событий m, благоприятствующих событию A, к числу всех элементарных событий
n:

Вероятность достоверного события равна 1.
Вероятность невозможного события равна 0.
Вероятность случайного события больше 0 и меньше 1.

Статистическое определение вероятности

Классическое определение вероятности не является пригодным для изучения
произвольных случайных событий. Например, оно неприемлемо, если результаты
испытания не равновозможны. В таких случаях используется статистическое
определение вероятности. Пусть проводится n опытов, событие A наступило
m раз, тогда

,

где m — абсолютная частота события A; P(A) — относительная частота
события A.
Вероятностью события А для испытания в данном опыте называется число
P(A), около которого группируются значения относительной частоты при
больших n.

Геометрическое определение вероятности

Если в результате проведения испытаний наблюдается произвольный исход
из некоторого бесконечного множества, то можно сказать, что пространство
элементарных исходов может быть некоторой областью G, а под событием
А можно понимать исходы, входящие в область g. Пусть на область G наугад
брошена «точка»; приняв равновозможность вариантов, естественно
считать, что вероятность попадания в область g можно найти по формуле,
называемой геометрической вероятностью:

Области могут быть различной размерности (одно-, двух- или трехмерного
измерения) и, в зависимости от выбора размерности меры, могут принимать
значения либо длины, либо площади, либо объема. Для конкретного испытания
размерность мер g и G должна быть одна.

Геометрическое определение

Геометрическое определение применяется для случая, когда количество равновозможных событий будет бесконечно. Здесь, для введения геометрического определения рассмотрим следующий пример. Для игры дартс берем круг площадью $S$ и разбиваем его на несколько кругов. Какова вероятность, что дротик попадет в центральный круг? (Исключим здесь случаи полного непопадания в поле). Очевидно что равновозможных событий здесь будет бесконечно (как и общих событий) так как круг содержит в себе бесконечное число точек. Пусть площадь центрального круга равняется $s$. Тогда мы сталкиваемся с геометрическим определением вероятности такого события:

$P(B)=\frac{s}{S}$

Алгебра событий

Операция сложения событий означает логическую связку ИЛИ, а операция умножения событий — логическую связку И.

Сложение событий

Суммой двух событий A и B называется событие A+B, которое состоит в том, что наступит или событие A, или событие B, или оба события одновременно. В том случае, если события несовместны, последний вариант отпадает, то есть может наступить или событие A, или событие B.

Правило распространяется и на большее количество слагаемых, например, событие A₁ + A₂ + A₃ + A₄ + A₅ состоит в том, что произойдет хотя бы одно из событий A₁, A₂, A₃, A₄, A₅, а если события несовместны — то одно и только одно событие из этой суммы: или событие A₁, или событие A₂, или событие A₃, или событие A₄, или событие A₅.

Примеров масса:

• Событие (при броске игральной кости не выпадет 5 очков) состоит в том, что выпадет или 1, или 2, или 3, или 4, или 6 очков.

Событие B_{1, 2} = B₁ + B₂ (выпадет не более двух очков) состоит в том, что появится 1 или 2 очка.

Событие B_Ч = B₂ + B₄ + B₆ (будет чётное число очков) состоит в том, что выпадет или 2 , или 4 , или 6 очков.

Умножение событий

Произведением двух событий A И B называют событие AB, которое состоит в совместном появлении этих событий. Иными словами, умножение AB означает, что при некоторых обстоятельствах наступит и событие A, и событие B. Аналогичное утверждение справедливо и для большего количества событий: например, произведение A₁A₂A₃ … A₁₀ подразумевает, что при определенных условиях произойдет и событие A₁, и событие A₂, и событие A₃,…, и событие A₁₀.

Рассмотрим испытание, в котором подбрасываются две монеты, и следующие события:

• A₁ — на 1-й монете выпадет орел;

Ā₁ — на 1-й монете выпадет решка;

A₂ — на 2-й монете выпадет орел;

Ā₂ — на 2-й монете выпадет решка.

Тогда:

• событие A₁A₁ состоит в том, что на обеих монетах (на 1-й и на 2-й) выпадет орел;

событие Ā₂Ā₂ состоит в том, что на обеих монетах (на 1-й и на 2-й) выпадет решка;

событие A₁Ā₂ состоит в том, что на 1-й монете выпадет орел и на 2-й монете решка;

событие Ā₁A₂ состоит в том, что на 1-й монете выпадет решка и на 2-й монете орел.

Несовместные и совместные события

Рассмотрим два события: “чайник исправно работает” и “чайник сломался”. Могут ли эти события существовать одновременно? Нет, поскольку появление одного из них исключает появление другого.

Такие события называются несовместными. Название само говорит, что события не могут существовать одновременно. 

Несовместные события — такие события, появление одного из которых исключает появление другого. 

Решим небольшую задачу. На экзамене есть несколько билетов. С вероятностью 0,5 попадется билет по планиметрии. С вероятностью 0,3 попадется билет по экономике. При этом не существует билетов, которые включают обе эти темы. С какой вероятностью на контрольной попадется билет по одной из этих тем?

Представим билеты в виде схемы. Заметим, что нам нужно объединить два из трех кругов, то есть сложить их вероятности. 

Следовательно, вероятность будет равна 0,5 + 0,3 = 0,8.

Сформулируем определение суммы вероятностей двух несовместных событий. 

Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей:\(P(A \cup B) = P(A) + P(B)\)

Если существуют несовместные события, то существуют и совместные. 

Совместные события — события, наступление одного из которых не исключает наступления другого. 

В магазине работают два консультанта. Один из них занят общением с клиентом. Означает ли это, что второй консультант тоже занят?  Нет, поскольку они работают независимо друг от друга. Если занят первый консультант, второй может быть как занят, так и нет. 

Подбросим игральный кубик и рассмотрим два вида событий. Пусть событие А — это “выпадет число 2”, событие В — “выпадет четное число”. 

Найдем вероятность события А: \(\frac{1}{6}\). 

Для события В всего три благоприятных исхода из шести: выпадет число 2, 4 или 6. Тогда вероятность наступления события В равна \(\frac{3}{6} = \frac{1}{2}\)

Исключают ли события А и В друг друга? Нет, поскольку если произойдет событие А, произойдет и событие В. Когда произойдет событие В, есть вероятность, что произойдет и событие А. 

Найдем объединение совместных событий на примере кругов. Если мы наложим их друг на друга, то в середине получится как бы два слоя. Проверить это можно, если наложить друг на друга два листа бумаги. 

А нужно получить вот такую картину:

Поэтому для объединения двух кругов нам нужно будет исключить одну из серединок. 

Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения:\(P(A \cup B) = P(A) + P(B) — P(A \cap B)\)

В каких случаях нужно пользоваться формулой со сложением? Достаточно, чтобы задачу можно было сформулировать с помощью “или”. Например, нужно, чтобы выпали темы по планиметрии или по экономике. 

Примеры по теме “Статистическое определение вероятности”

Пример 1

Задача

Статистическая вероятность попадания в цель при 84 выстрелах равна 0,9. Сколько всего было попаданий?

Решение

Так как у нас есть формула , где – число попаданий, – число выстрелов, тогда . Подставляя исходные данные, у нас получается:

Ответ

Итого попаданий – 75,6.

Пример 2

Задача

Швейная фабрика заказала 3500 пуговиц, чтобы пошить школьную форму. Когда проверяли партию на 700 пуговиц, оказалось, что из них 15 пуговиц бракованных. Какое наименьшее количество запасных пуговиц необходимо еще заказать, чтобы исключить брак?

Решение

Статистическая частота брака составляет , тогда среди 3500 пуговиц, бракованных . Значит, необходимо заказать наименьшее количество запасных пуговиц 75 шт.

Ответ

Чтобы исключить брак, нужно заказать минимум 75 шт. запасных пуговиц.

Классическое определение

Классическое определение связано с такими неопределяемыми понятиями как равновозможность и элементарность события. Интуитивно их можно понять на следующих примерах:

Равновозможность: При подбрасывании монеты она может упасть как аверсом, так и реверсом независимо от внешних условий. То есть можно сказать что вероятность выпадения одной или другой стороны по сути одинакова.

Элементарность события: Если на кости выпадет число $4$, то это означает, что числа $1, 2, 3, 5$ и $6$ уже не выпали.

Определение 5

Вероятностью события будем называть отношения числа n равновозможных элементарных событий исходного события $B$ ко всем элементарным событиям $N$.

Математически это выглядит следующим образом:

$P(B)=\frac{n}{N}$

Понятие вероятности события

Определение 2

Вероятностью события будем называть число, которое обозначает степень возможности, что такое событие произойдет.

Вероятность события обозначается как $P(A)$

Чтобы определить границы значения этого числа введем понятие достоверного и невозможного событий.

Определение 3

Достоверным событием будем называть такое, которое произойдет при любых обстоятельствах.

Примером такого события может быть следующее: Сумма «точек» на классической кости всегда равняется $21$.

Вероятность такого события мы будем принимать за единицу.

Определение 4

Невозможным событием будем называть такое, которое не может произойти ни при каком обстоятельстве.

Примером такого события может быть следующее: При игре в «очко» игрок набрал $1$ очко.

Вероятность такого события мы будем принимать за $0$.

То есть значение вероятности любого события содержится в отрезке $$.

В современной теории вероятности принято выделять четыре определения для вероятности: классической, геометрическое, статистическое и аксиоматическое определения. Рассмотрим их отдельно.