Анализ качества модели линейной регрессии
Метод наименьших квадратов имеет по меньшей мере один существенный недостаток: с его
помощью можно найти уравнение линейной регрессии и в тех случаях, когда данные наблюдений значительно
рассеяны вокруг прямой регрессии, то есть находятся на значительном расстоянии от этой прямой. В таких
случаях за точность прогноза значений зависимой переменной ручаться нельзя. Существуют показатели,
которые позволяют оценить качество уравнения линейной регрессии прежде чем использовать модели линейной
регрессии для практических целей. Разберём важнейшие из этих показателей.
Коэффициент детерминации
Коэффициент детерминации
принимает значения от 0 до 1 и в случае качественной модели линейной регрессии стремится к единице.
Коэффициент детерминации показывает, какую часть общего рассеяния зависимой переменной объясняет независимая переменная:
,
где
—
сумма квадратов отклонений, объясняемых моделью линейной регрессии, которая характеризует рассеяние
точек прямой регрессии относительно арифметического среднего,
—
общая сумма квадратов отклонений, которая характеризует рассеяние зависимой переменной Y
относительно арифметического среднего,
—
сумма квадратов отклонений ошибки (не объясняемых моделью линейной регрессии), которая характеризует
рассеяние зависимой переменной Y относительно прямой регресии.
Пример 3. Даны сумма квадратов отклонений, объясняемых моделью линейной
регрессии (3500), общая сумма квадратов отклонений (5000) и сумма квадратов отклонений ошибки (1500).
Найти коэффициент детерминации двумя способами.
F-статистика (статистика Фишера) для проверки качества модели линейной регрессии
Минимальное возможное значение F-статистики — 0. Чем выше значение статистики Фишера,
тем качественнее модель линейной регрессии. Этот показатель представляет собой отношение объясненной
суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на
одну степень свободы):
где m — число объясняющих переменных.
Сумма квадратов остатков
Сумма квадратов остатков (RSS) измеряет необъясненную часть дисперсии
зависимой переменной:
где
—
остатки — разности между реальными значениями зависимой переменной и значениями,
оценёнными уравнением линейной регрессии.
В случае качественной модели линейной регрессии сумма квадратов остатков стремится
к нулю.
Стандартная ошибка регрессии
Стандартная ошибка регрессии (SEE) измеряет величину квадрата ошибки,
приходящейся на одну степень свободы модели:
Чем меньше значение SEE, тем качественнее модель.
Пример 4. Рассчитать коэффициент детерминации для данных из примера 1.
Решение. На основании данных таблицы (она была приведена в примере урока о корреляционной
зависимости) получаем, что ,
, .
Можем убедиться, что выполняется закономерность :
.
Получаем коэффициент детерминации:
.
Таким образом, 83,6% изменений частного потребления можно объяснить моделью линейной
регресии.
Общие сведения о парной (простой) регрессии и её роли в экономике
Изучение предметов и явлений, которые имеют место быть в экономике, осуществляется во многом благодаря использованию широкого аппарата эконометрической науки. Она базируется на применении методов математического исследования в целях объяснения и прогнозирования экономических событий.
Если объекты экономической действительности выразить количественно, то эконометрика предоставляет возможность установить существование или отсутствие связи между ними, определить направление такой связи и оценить её силу. Для этого необходимо воспользоваться методами корреляционно-регрессионного анализа.
Как правило, в подобных исследованиях изучается то, как на один параметр (зависимую переменную, результат) оказывают влияние другие параметры (независимые переменные, факторы). Если одновременно изучается два или более фактора, то имеют дело с, так называемой, множественной регрессией.
Определение 1
Парная (простая) регрессия представляет собой эконометрическую модель, в которой значение зависимой переменной Y объясняется значением одной независимой переменной X. То есть объясняемая переменная зависит от объясняющей переменной, что можно выразить следующей функцией: Y = f (X).
Использование парной регрессии оправдано в случае наличия доминирующего фактора, который в среднем по совокупности наблюдений объясняет большую часть изменения итогового результата. На основании этой зависимости ученые получают возможность выделить, сформулировать и обосновать некоторую закономерность, существующую в текущей экономической действительности.
Наиболее известным примером использования парной регрессии для объяснения экономических явлений является зависимость спроса на товар Y от цены на него X, которая, например, может быть описана уравнением Y = 3000 – 4 ⋅ X. Оно означает, что, если цена возрастет на 1 денежную единицу, то спрос в среднем снизится на 4 условные единицы.
Стоит отметить, что данная математическая функция выражает функциональную связь исследуемых признаков. Однако на них оказывают влияние (пусть и не большое) ряд других факторов. Тогда фактическое значение результативного признака будет складываться из двух слагаемых: Y = Yi + e, где Yi – это теоретическое значение результативного признака, найденное из уравнения парной регрессии, е – это случайная величина, которая характеризует отклонение реального значения результативного признака от теоретического.
Присутствие в регрессионной модели случайной величины е (также называется возмущением) обусловлено:
- влиянием факторов, не учтенных из-за спецификации модели;
- случайными ошибками, вызванными выборочным характером исходных данных;
- особенностями измерения переменных.
Таким образом, в ситуации действия случайных факторов уравнение зависимости спроса от цены следует записать следующим образом: Y = 3000 – 4 ⋅ X + е.
Понятие линейной регрессии
Определение 1
Линейная регрессия – это математический метод установления зависимости между двумя переменными.
Теоретическая экономика строится на математических вычислениях и моделировании, которые позволяют описывать события, явления, динамику их изменения. Так же язык математики позволяет прогнозировать будущее положение экономических систем, субъектов и объектов.
Теория вероятности использует регрессию, как метод математической статистики. Она позволяет выявить прямую зависимость между величинами случайной природы. Основным отличием регрессии от функциональной зависимости является факт того, что одному и тому же значению искомой переменной может соответствовать множество других переменных.
Линейная регрессия представляет зависимость в виде линейной модели с учетом ошибки распределения. При этом значения каждой величины заранее неизвестны. Параметры для уравнения описывают выборочные оценки, важные для конкретного исследования. Обычно для исчисления используются экспериментальные данные.
Модель линейной регрессии активно применяется в эконометрике. Она удобна для изучения свойств оценок параметров, а так же для исследования случайных ошибок модели. С точки зрения эконометрической науки линейность чаще всего применяется для параметров, а не для факторов. Линейная модель может иметь константу, либо рассматриваться без нее. В этом случае первый фактор модели будет равным единице, либо останется обычным фактором.
Существует частный случай парной простейшей регрессии. В этом случае на модель воздействует только один фактор. Если количество факторов увеличивается, что регрессия становится множественной. В практической деятельности линейную регрессию применятся для расчета затрат организации, потребительских расходов.
Интерпретация коэффициентов уравнения парной линейной регрессии и прогноз значений зависимой переменной
Итак, уравнение парной линейной регрессии:
.
В этом уравнении a — свободный член, b — коэффициент при
независимой переменной.
Интерпретация свободного члена: a показывает, на сколько единиц график
регрессии смещён вверх при x=0, то есть значение переменной y при нулевом значении
переменной x.
Интерпретация коэффициента при независимой переменной: b показывает,
на сколько единиц изменится значение зависимой переменной y при изменении x на одну
единицу.
Пример 5. Зависимость частного потребления граждан от ВВП (истолкуем это просто: от дохода)
описывается уравнением парной линейной регрессии .
Сделать прогноз потребления при доходе в 20 000 у.е. Выяснить, на сколько увеливается потребление при
увеличении дохода на 5000 у.е. Меняется ли потребление, если доход не меняется?
Решение. Подставляем в уравнение парной линейной регрессии
и получаем прогноз потребления при доходе в 20 000 у.е. .
Подставляем в уравнение парной линейной регрессии
и получаем прогноз увеличения потребления при увеличении дохода на 5000 у.е. .
Если доход не меняется, то
и получаем, что потребление уменьшается на 129,5338 у.е.
Проверка гипотезы о равенстве нулю коэффициента направления прямой парной линейной регрессии
Одна из важнейших гипотез в регрессионном анализе — гипотеза о том, что коэффициент
направления прямой регрессии генеральной совокупности
равен нулю.
Если это предположение верно, то изменения независимой переменной X не
влияют на изменения зависимой переменной Y: переменные X и Y не коррелированы,
то есть линейной зависимости Y от X нет.
Нулевую гипотезу
рассматривают во взаимосвязи с альтернативной гипотезой
.
Статистика коэффициента направления
соответствует распределению Стьюдента с числом степеней свободы ,
где —
стандартная погрешность коэффициента направления прямой линейной регресии .
Доверительный интервал коэффициента направления прямой линейной регрессии:
.
Критическая область, в которой с вероятностью
отвергают нулевую гипотезу и принимают альтернативную гипотезу:
Пример 6. На основе данных из предыдущих примеров (о ВВП и частном
потреблении) определить доверительный интервал коэффициента направления прямой линейной регресии 95% и
проверить гипотезу о равенстве нулю коэффициента направления прямой парной линейной регрессии.
Можем рассчитать, что ,
а стандартная погрешность регрессии .
Таким образом, стандартная погрешность коэффициента направления прямой линейной регресии
:
.
Так как и
(находим по таблице
в приложениях к учебникам по статистике), то доверительный интервал 95% коэффициента направления прямой
парной линейной регрессии:
.
Так как гипотетическое значение коэффициента — нуль — не принадлежит доверительному
интервалу, с вероятностью 95% можем отвергнуть основную гипотезу и принять альтернативную гипотезу,
то есть считать, что зависимая переменная Y линейно зависит от независимой переменной X.
| Назад | Листать | Вперёд>>> |
Всё по теме «Математическая статистика»
Понятие линейной регрессии. Парная линейная регрессия
Линейная регрессия — выраженная в виде прямой зависимость среднего значения какой-либо
величины от некоторой другой величины. В отличие от функциональной зависимости ,
когда каждому значению независимой переменной x соответствует одно определённое значение
величины y, при линейной регрессии одному и тому же значению x могут соответствовать
в зависимости от случая различные значения величины y.
Если в результате наблюдения установлено,
что при каждом определённом значении x существует сколько-то (n) значений переменной
y, то зависимость средних арифметических значений y от x и является регрессией
в статистическом понимании.

Если установленная зависимость может быть записана в виде уравнения прямой
,
то эта регрессионная зависимость называется линейной регрессией.
О парной линейной регрессии говорят, когда установлена зависимость между двумя
переменными величинами (x и y). Парная линейная регрессия называется также однофакторной
линейной регрессией, так как один фактор (независимая переменная x) влияет на результирующую
переменную (зависимую переменную y).
В уроке о корреляционной зависимости
были разобраны примеры того, как цена на квартиры зависит от общей площади квартиры и от площади
кухни (две различные независимые переменные) и о том, что результаты наблюдений расположены в некотором
приближении к прямой, хотя и не на самой прямой. Если точки корреляционной диаграммы соединить ломанной
линией, то будет получена линия эмпирической регрессии. А если эта линия будет выровнена в прямую, то
полученная прямая будет прямой теоретической регрессии. На рисунке ниже
она красного цвета (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши).
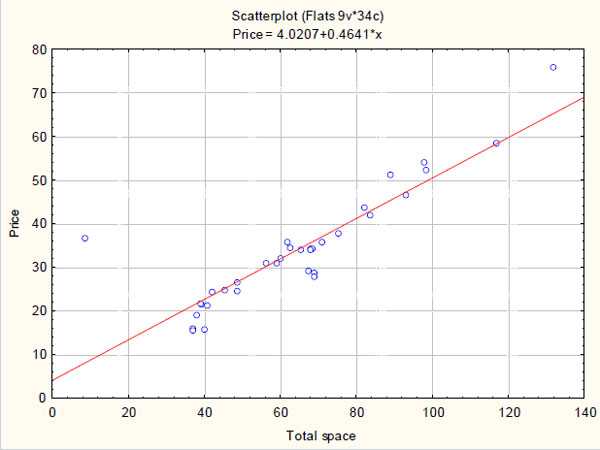
По этой прямой теоретической регрессии может быть сделан прогноз или восстановление
неизвестных значений зависимой переменной по заданным значениям независимой переменной.
В случае парной линейной регрессии для данных генеральной совокупности связь между
независимой переменной (факториальным признаком) X и зависимой переменной (результативным
признаком) Y описывает модель
,
где
—
свободный член прямой парной линейной регрессии,
—
коэффициент направления прямой парной линейной регрессии,
—
случайная погрешность,
N — число элементов генеральной совокупности.
Уравнение парной линейной регрессии для генеральной совокупности можно построить, если
доступны данные обо всех элементах генеральной совокупности. На практике данные всей генеральной совокупности
недоступны, но доступны данные об элементах некоторой выборки.
Поэтому параметры генеральной совокупности оценивают при помощи соответствующих
параметров соответствующей выборки: свободный член прямой парной линейной регрессии генеральной совокупности
заменяют на
свободный член прямой парной линейной регрессии выборки ,
а коэффициент направления прямой парной линейной регрессии генеральной совокупности
— на коэффициент
направления прямой парной линейной регрессии выборки
.
В результате получаем уравнение парной линейной регрессии выборки
или
где
—
оценка полученной с помощью модели линейной регрессии зависимой переменной Y,
—
погрешность,
n — размер выборки.
Чтобы уравнение парной линейной регрессии было более похоже на привычное уравнение
прямой, его часто также записывают в виде
.






























