Слайд 15Граничные условия III рода. В этом случае задаются температура среды
Tж и условия теплообмена этой среды с поверхностью тела. Процессы
теплообмена между средой и телом являются исключительно сложными и зависят от многих факторов.Для описания интенсивности теплообмена между поверхностью тела и окружающей средой используется гипотеза Ньютона-Рихмана, согласно которой
где — коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м2К).Как следует из формулы (27), коэффициент теплоотдачи численно равен количеству теплоты, отдаваемого (или воспринимаемого) единицей поверхности тела в единицу времени при разности температур между поверхностью тела и окружающей средой, равной 1 К. С учетом уравнений (3) и (27) граничное условие III рода записывается в виде
Когда коэффициент теплоотдачи имеет большие значения (например, при кипении жидкости на поверхности тела), граничные условия III рода переходят в граничные условия I рода, так как в этом случае температура поверхности тела становится практически равной температуре жидкости.Граничные условия IV poдa формулируются на основании равенства тепловых потоков, проходящих через поверхность соприкосновения тел, т.е.
(27)
(28)
(29)

Слайд 8где w — средняя скорость перемещения молекул; l — средняя
длина свободного пробега молекул; Cv — теплоемкость. С
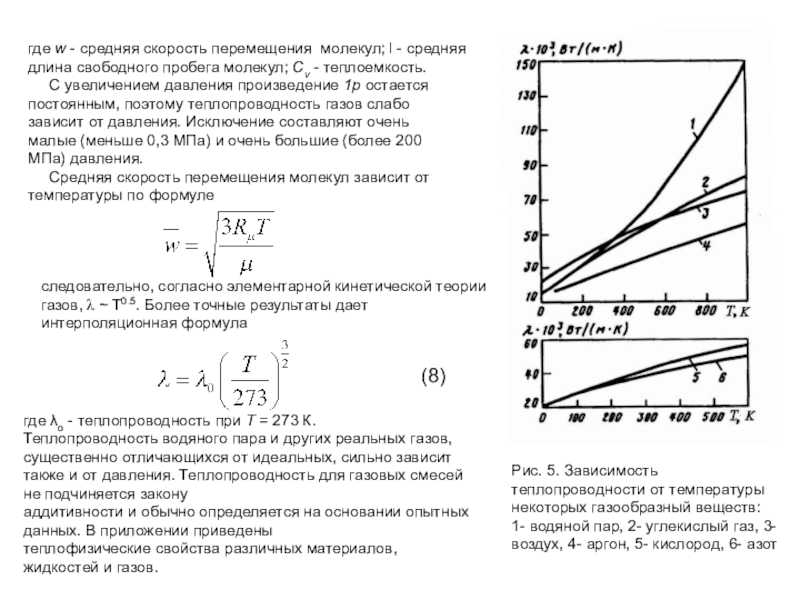
увеличением давления произведение 1р остается постоянным, поэтому теплопроводность газов слабо зависит от давления. Исключение составляют очень малые (меньше 0,3 МПа) и очень большие (более 200 МПа) давления. Средняя скорость перемещения молекул зависит от температуры по формуле
следовательно, согласно элементарной кинетической теории газов, l ~ T0.5. Более точные результаты дает интерполяционная формула
где λо — теплопроводность при Т = 273 К.Теплопроводность водяного пара и других реальных газов, существенно отличающихся от идеальных, сильно зависит также и от давления. Теплопроводность для газовых смесей не подчиняется закону аддитивности и обычно определяется на основании опытных данных. В приложении приведены теплофизические свойства различных материалов, жидкостей и газов.
(8)
Рис. 5. Зависимость теплопроводности от температуры некоторых газообразный веществ: 1- водяной пар, 2- углекислый газ, 3- воздух, 4- аргон, 5- кислород, 6- азот
Слайд 4которая носит название закона Фурье. Знак минус указывает на то,
что векторы плотности теплового потока и градиента температур, в соответствии
со II законом термодинамики, направлены в противоположные стороны, а множитель пропорциональности рассматривается как некоторая физическая характеристика, именуемая теплопроводностью. Кроме того, отметим, что производная температуры по направлению I определяется через производные температуры по декартовым координатам формулой
где cos(x, /), cos(y, l) и соs(г, /) — косинусы углов между направлением / и координатными осями OX, OY, 0Z. С учетом (4) закон Фурье (2) можно записать в виде:
где dS = dF • cos(n, /) — элементарная площадка, перпендикулярная направлению /.
(5)
(6)

Температурный градиент. Процесс теплопроводности, как и другие виды теплообмена, может иметь место только при условии, что в различных точках тела (или системы тел) температура
Температурное поле
Процесс теплопроводности, как и другие виды теплообмена, может иметь место только при условии, что в различных точках тела (или системы тел) температура неодинакова. В общем случае процесс распространения теплоты теплопроводностью в теле сопровождается изменением температуры, как в пространстве, так и во времени. Температурное состояние тела (или системы тел) можно охарактеризовать с помощью температурного поля.
Температурным полем называют совокупность значений температуры во всех точках тела для каждого времени.
Поскольку температура различных точек тела определяется координатами x, y, z и временем τ, то в общем случае уравнение температурного поля имеет вид:
(1)
Различают стационарные и нестационарные температурные поля. Если температура в точках тела не изменяется во времени, то такое температурное поле называют стационарным или установившимся, если же температура меняется во времени, то поле называют нестационарным или неустановившимся.
Температура в теле может меняться в направлении одной, двух или трех координатных осей. В соответствии с этим различают одномерные (линейные), двухмерные (плоскостные) и трехмерные (пространственные) температурные поля.
В соответствии с изложенной классификацией температурных полей уравнение (1) описывает трехмерное нестационарное поле.
Уравнение трехмерного стационарного поля имеет вид:
; (2)
Уравнение одномерного нестационарного поля принимает вид:
; (3)
Наиболее простой вид имеет уравнение одномерного стационарного температурного поля:
; ; (4)
Температурный градиент
Геометрическое место точек в температурном поле, имеющих одинаковую температуру, называется изотермической поверхностью.
Так как одна и та же точка тела не может одновременно иметь различные температуры, то изотермические поверхности не пересекаются, они либо обрываются на поверхности тела, либо замыкаются сами на себя внутри тела. Пересечение изотермических поверхностей плоскостью дает на этой плоскости семейство изотерм, которые обладают теми же свойствами, что и изотермические поверхности.
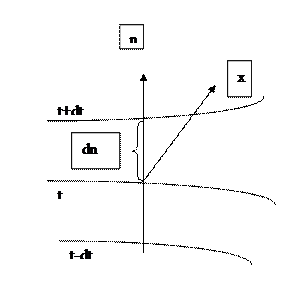
На рис.1 приведены изотермы, температуры которых отличаются на Δt. Температура в теле изменяется только в направлениях, пересекающих изотермические поверхности (направление x). При этом наибольший перепад температуры на единицу длины происходит в направлении нормали n к изотермической поверхности. Предел отношения изменения температуры Δt к расстоянию между изотермами по нормали Δn при условии, что Δn→ 0 , называют температурным градиентом, т.е.
(5)
Температурный градиент — векторная величина. За положительное направление вектора gradt принимается направление по нормали к изотермической поверхности в сторону возрастания температуры. Скалярную величину gradt мы также будем называть температурным градиентом. Значение gradt не одинаково для различных точек изотермической поверхности, оно больше там, где расстояние между изотермическими поверхностями меньше.
Проекции вектора gradt на координатные оси Ox, Oy, Oz равны:
(6)
Слайд 16При совершенном тепловом контакте оба тела на поверхности соприкосновения имеют
одинаковую температуру, т.е. изотермы непрерывно переходят из одного тела в
другое, а градиенты температур в этих точках удовлетворяют условию (29). В реальных конструкциях тепловой контакт между соприкасающимися деталями обычно нельзя считать идеальным, так как действительная поверхность контакта составляет только малую часть всей поверхности, даже если эти поверхности гладкие, и сжимающая сила велика. Если коэффициенты теплопроводности находящихся в контакте тел существенно выше, чем теплопроводность среды, заполняющей полости, то основная часть теплоты будет передаваться через точки контакта. Различие температур соприкасающихся поверхностей пропорционально контактному термическому сопротивлению или обратно пропорционально контактной тепловой проводимости, которая количественно характеризуется коэффициентом В этом случае условие (29) принимает вид
Коэффициент контактного теплообмена зависит от множества факторов и его определение является сложной задачей. Из сопоставления формул (26), (28) и (29) следует, что они различаются правыми частями уравнений. Исключение составляет граничное условие I рода, которое задается температурой поверхности тела. Однако можно показать, что граничное условие III рода преобразуется в граничное условие I рода при —►∞ , т.е. при очень интенсивной теплоотдаче. Тогда из уравнения (27) следует, что Tcт = TЖ. Граничные условия могут существенно усложниться процессами радиационного теплообмена, процессами массообмена с фазовыми переходами и т.п. Дифференциальное уравнение (17) совместно с условиями однозначности дает полную математическую формулировку конкретной задачи теплопроводности. Решение этой задачи может быть выполнено аналитически, численным или экспериментальным методом. В последнем случае используются методы физического подобия и аналогий.































