Вероятность в термодинамике

Особенности вероятности в термодинамике

Рисунок 2. Термодинамическая вероятность. Автор24 — интернет-биржа студенческих работ

Замечание 1

Основное достоинство термодинамики заключается в том, что она помогает рассмотреть общие свойства концепции при равновесии и общие закономерности определения плотности, получить важные сведения о самом веществе, не зная в полной мере его начальную внутреннюю структуру.

Ее законы и методы применимы к любому материальному телу, к любым системам, которые включают магнитные и электрические поля, поэтому они стали основами в таких сферах:

• газовых и конденсированных сред;
• химии и техники;
• необходимыми в физике Вселенной и геофизике;
• биологии и управлений физическими процессами.

Исследователь Больцман считал атомистическую теорию вполне обоснованной. Бесконечное или огромное количество частиц делает невозможным механический эффект, нуждается в статистическом описании. Математическим инструментом современной статистики является исчисление и определение вероятностей. Больцман доказал, что поскольку базой термодинамических процессов выступают кинетические обратимые процессы, то необратимость в измеряемой термодинамикой энтропии, не может быть на практике абсолютной. Поэтому и энтропия должна быть непосредственно связана с возможностью осуществления данного микросостояния.

Понятие вероятности, неявно применяемого Максвеллом, Больцман использовал для преодоления трудностей, имеющих отношение к пониманию второго начала термодинамики и теории «тепловой смерти Вселенной». Вершиной научной работы Больцмана стало установление взаимосвязи между термодинамической вероятностью и энтропией. Планк представил эту связь через введение константы $k = R / N$, которая носит название постоянной Больцмана.

Таким образом, необратимый физический процесс есть плавный переход из менее вероятного положения в более вероятное, а логарифм изменения начального состояния с точностью до стабильного множителя полностью совпадает с перемещением энтропии. Этот эффект Больцман использовал для идеального газа.

Чем выше уровень беспорядка в скоростях и координатах частиц системы, тем больше возможность того, что концепция будет в состоянии хаоса. Формула Больцмана может рассматриваться как основное определение энтропии.

Различие термодинамической и математической систем

На сегодняшний день ученые разделяют две основные вероятности в термодинамике:

• математическую;
• термодинамическую.

Термодинамической вероятностью называется определенной число микросостояний, посредством которых можно провести необходимое макросостояние концепции. Чтобы найти термодинамическую вероятность ее начального состояния, следует подсчитать количество комбинаций, которые помогут осуществить любое пространственное распределение элементарных частиц.

Замечание 2

Этот параметр определяется числом перестановок из наличного движения частиц.

Математическая вероятность состояния равна отношению термодинамической возможности к общей величине возможных микросостояний. Математическая вероятность всегда меньше одной единицы, между тем как вероятность в термодинамике выражается большими числами. Вероятность в математике не аддитивна и непосредственно связана не с термическими особенностями системы, а с механическими, например, с движением молекул в среде и их скоростью. 

Одному и тому макросостоянию может соответствовать множество второстепенных микросостояний. По Л. Больцману, чем большим числом таких положений может реализоваться конкретное макросостояние, тем оно на практике более вероятно. Термодинамической вероятностью состоянию концепции называется число микросостояний, реализующих в итоге макросостояние.

При пользовании указанных способов необходимо иметь в виду, что основанные на ней выводы считаются наиболее вероятными только в термодинамическом вопросе, и указывают только на возможность или невозможность того или иного физического процесса. В реальных условиях не исключены незначительные отклонения от сделанных выводов, и протекающие явления могут при отдельных обстоятельствах быть иными, чем те, которые действовали исходя из общих термодинамических соображений.

Энтропия и вероятность состояния

Известно, что любая система без воздействия на нее извне стремится прийти в состояние, характеризуемое минимумом ее потенциальной энергии. Эта информация позволяет в некоторой мере предсказывать направление протекания того или иного процесса в естественных условиях «без воздействия на тело или систему извне. Кроме того, как показал Клаузиус, реальные процессы всегда развиваются таким образом, что одна из важнейших характеристик состояния системы — энтропия — возрастает. Следовательно, любая термодинамическая система будет развиваться в направлении минимума потенциальной энергии и максимума энтропии. Но не только потенциальная энергия и энтропия могут помочь в определении направления протекания реальных процессов. Существует еще один, статистический, закон природы, в котором утверждается, что наиболее вероятным является состояние с максимальным беспорядком.

Рассмотрим сосуд, состоящий из нескольких соединенных между собой ячеек. Поместим в этот сосуд n молекул, которые могут свободно перемещаться по сосуду из ячейки в ячейку, распределяясь каким угодно образом. Характер этого распределения может быть самым разнообразным. В качестве примера рассмотрим распределение шести молекул в сосуде из трех ячеек. Несложные рассуждения убедят нас в том, что возможны различные способы распределения молекул по ячейкам, часть которых показана на рисунке 9. В качестве примера рассмотрим такую ситуацию. Ящик разделен перегородками на три отсека. Пусть в одном из них находятся молекулы; два других — пустые. Такую систему частиц можно считать упорядоченной. Убрав перегородки между отсеками, мы заметим, что молекулы, участвуя в хаотическом тепловом движении, через некоторое время займут весь предоставленный им объем. Наблюдая далее, мы увидим, что молекулы перераспределились так, что в каждом из отсеков содержится примерно одинаковое число молекул, хотя неизбежны и некоторые отклонения — флуктуации, которые будут тем меньше, чем больше исходное число молекул в ящике. Таким образом, система, предоставленная самой себе, приходит в наиболее вероятное состояние: одинаковое число молекул в каждом отсеке. Этот процесс перераспределения развивается в таком направлении, следуя которому энтропия возрастает; при этом система приходит к наиболее вероятному состоянию. Иначе, возрастание энтропии связано с увеличением вероятности состояния. Количественной характеристикой вероятности того или иного состояния является термодинамическая вероятность, которая представляет собой не что иное, как число способов, которыми может быть реализовано состояние данной физической системы. Распределение, соответствующее рисунку 9, является наиболее вероятным.

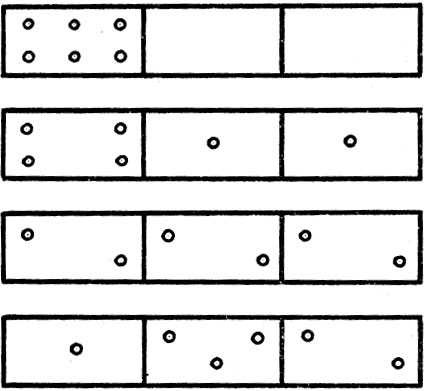Рис. 9. Способы распределения молекул по ячейкам

Изучая термодинамические процессы, Больцман заметил общность в направлении изменения энтропии некоторой системы и в значении термодинамической вероятности состояния. Он установил, что энтропия некоторой термодинамической системы пропорциональна логарифму вероятности ее состояния. Повышение энтропии означает нарушение упорядочения, стремление системы к хаотическому движению частиц, ее образующих. Согласно теоретическим исследованиям Больцмана

Согласно теоретическим исследованиям Больцмана (34)

где S — энтропия системы; W — термодинамическая вероятность ее состояния.

Развивая далее представления Больцмана о связи энтропии и вероятности состояния, немецкий физик М. Планк нашел коэффициент пропорциональности в соотношении (34) и получил равенство

Коэффициент пропорциональности (35)

где k — константа, получившая впоследствии название постоянной Больцмана.

Из работ Больцмана и Планка следует, что второе начало термодинамики, так же как и первое, является статистическим законом. Второе начало термодинамики справедливо только для большого числа молекул, к которому можно применить статистические методы. Установленный Клаузиусом закон возрастания энтропии следует понимать как среднестатистический вывод. В отдельных частях системы могут протекать процессы, развивающиеся так, что энтропия этой части системы может убывать, хотя в целом макросистема характеризуется ростом энтропии. Эти флуктуации энергии, плотности, температуры непрерывно возникают и исчезают через сравнительно малые промежутки времени. Наиболее вероятное состояние означает то, что система находится в состоянии термодинамического равновесия. Соотношение между энтропией и термодинамической вероятностью позволяет утверждать, что энтропия представляет собой меру близости изолированной системы к состоянию термодинамического равновесия.

Термодинамическая вероятность — состояние

Термодинамическая вероятность состояния W и энтропия изолированной системы 5 являются различными мерами стремления системы к равновесию. Обе величины возрастают при необратимых процессах, приближающих систему к равновесию, и достигают максимума при равновесном состоянии системы. Между величинами W и S имеется количественная связь. Общий вид этой связи нетрудно установить, если учесть аддитивность энтропии, которая является суммой энтропии отдельных частей равновесной системы, и мультипликативность вероятности сложного события, которая является произведением вероятностей отдельных независимых событий.
 

Термодинамическая вероятность состояния W и энтропия изолированной системы 5 являются различными мерами стремления системы к равновесию. Обе величины возрастают при необратимых процессах, приближающих систему к равновесию, и достигают максимума при равновесном состоянии системы. Между величинами W и S имеется количественная связь. Общий вид этой связи нетрудно установить, если учесть аддитивность энтропии, которая является суммой энтропии — отдельных частей равновесной системы, и мультипликативность вероятности сложного события, которая является произведением вероятностей отдельных независимых событий.
 

Термодинамическая вероятность состояния W и энтропия изолированной системы S являются различными мерами стремления системы к равновесию. Обе величины возрастают при необратимых процессах, приближающих систему к равновесию, и достигают максимума при равновесном состоянии системы. Между величинами W и 5 имеется количественная связь. Обший вид этой связи нетрудно установить, если учесть аддитивность энтропии, которая является суммой энтропии отдельных частей равновесной системы, и мультипликативность вероятности сложного события, которая является произведением вероятностей отдельных независимых событий.
 

Термодинамической вероятностью состояния называется число микросостояний системы, соответствующих данному макросостоянию ( стр. Величина Р для химически однородной системы показывает, сколькими способами может быть реализовано заданное количественное распределение частиц по ячейкам фазового пространства безотносительно к тому, в какой ячейке находится та или иная конкретная частица.
 

Термодинамической вероятностью состояния системы называется число микросостояний, посредством которых данное состояние может осуществиться. Применяя теорию вероятностей, законы которой в сочетании с законами механики образуют статистическую механику, можно, с одной стороны, определить связь термодинамической вероятности с энтропией, а с другой — определить термодинамическую вероятность состояния.
 

Определяем термодинамическую вероятность W состояния системы из ЗА / осцилляторов, получивших всего п квантов энергии. Эти п квантов могут распределиться между 3N степенями свободы разными способами.
 

Под термодинамической вероятностью состояния подразумевается числитель дроби, выражающей вероятность этого состояния в обычном ее понимании.
 

Количественной мерой термодинамической вероятности состояния w является число различных микросостояний, которыми может быть осуществлено макросостояние, характеризуемое заданными термодинамическими параметрами.
 

Что называется термодинамической вероятностью состояния и как она связана с энтропией.
 

Исходным понятием является термодинамическая вероятность состояния системы W.
 

Рассмотрим теперь связь термодинамической вероятности состояния системы с энтропией.
 

Больцмана; W — термодинамическая вероятность состояния, определяемая числом микросостояний, реализующих данное микросостояние. Соотношение (3.49) выражает принцип Болъцмана. Односторонний характер изменения энтропии в замкнутой системе определяется переходом системы из менее вероятного состояния в более вероятное.
 

Больцмана; ш — термодинамическая вероятность состояния, определяемая числом микросостояний, реализующих данное макросостояние. Соотношение (3.49) выражает принцип Больцмана. Односторонний характер изменения энтропии — в замкнутой системе определяется переходом системы из менее вероятного состояния в более вероятное.
 

Энтропия S связана с термодинамической вероятностью состояния W известным соотношением Sk nW, где k — постоянная Больцмана.
 

Статистическим весом О или термодинамической вероятностью состояния термодинамической системы называется число микросостояний, с помощью которых реализуется данное макросостояние.