Metodichka_81_Laboratornye_po_fizike / Маятник Обербека
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ СИСТЕМЫ ТЕЛ
С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА.
Цель работы – определить момент инерции системы четырех одинаковых грузов массы m двумя способами: 1) экспериментально с помощью маятника Обербека, 2) теоретически, считая грузы материальными точками. Сравнить полученные результаты.
Приборы и принадлежности: маятник Обербека, секундомер, масштабная линейка, набор грузов, штангенциркуль.
Момент инерции – физическая величина, характеризующая инертность тела при вращательном движении.
Моментом инерции материальной точки относительно оси вращения называется произведение массы этой точки на квадрат ее расстояния до оси (см. рис. 1)
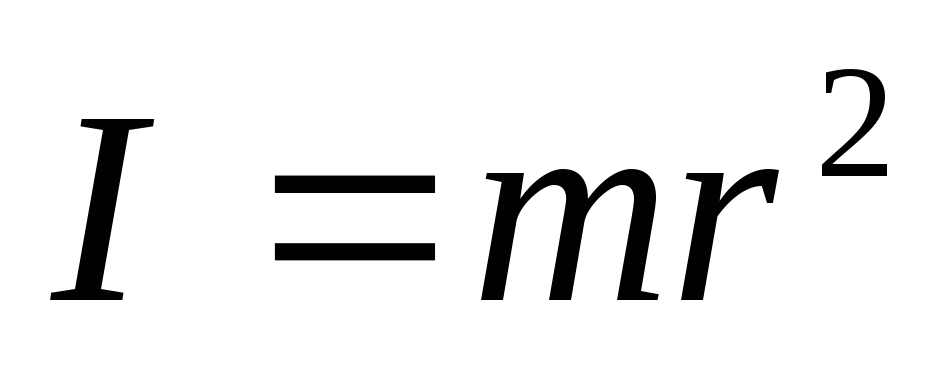
Моментом инерции произвольного тела относительно оси называется сумма моментов инерции материальных точек из которых состоит тело, относительно этой оси (см. рис. 2)
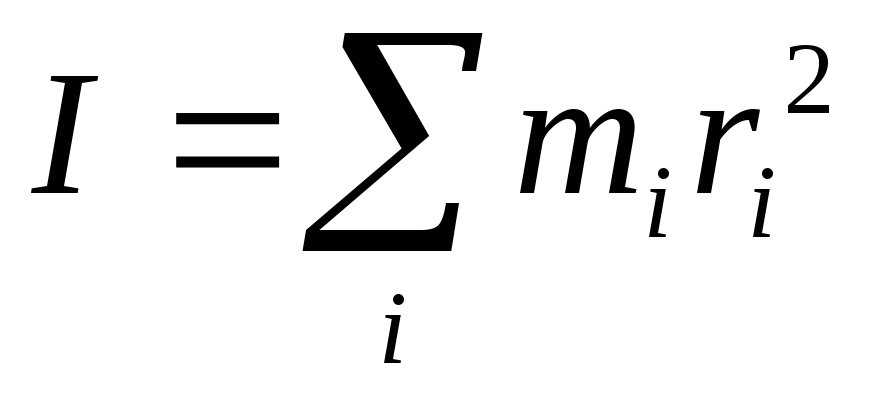
Для однородных тел правильной геометрической формы можно заменить суммирование интегрированием.
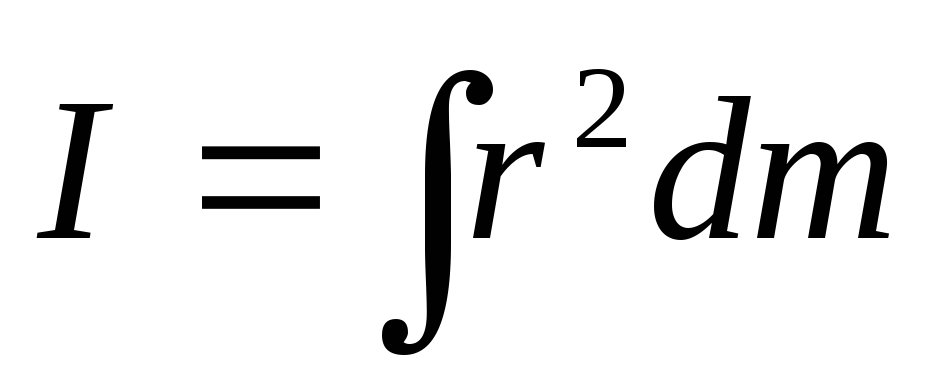
где dm = ρdV (ρ – плотность вещества, dV– элемент объема)
Таким образом получены формулы некоторых тел массой m относительно оси, проходящей через центр тяжести:
а) стержня длиной
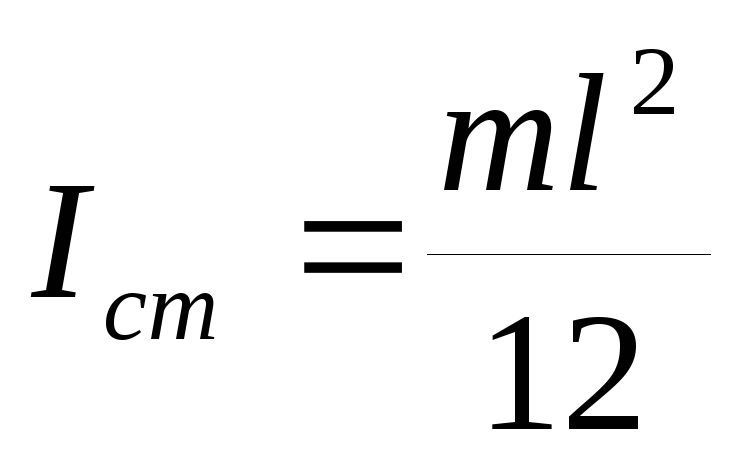
б) обруча (а также тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча и проходящей через его центр тяжести (совпадающей с осью цилиндра)
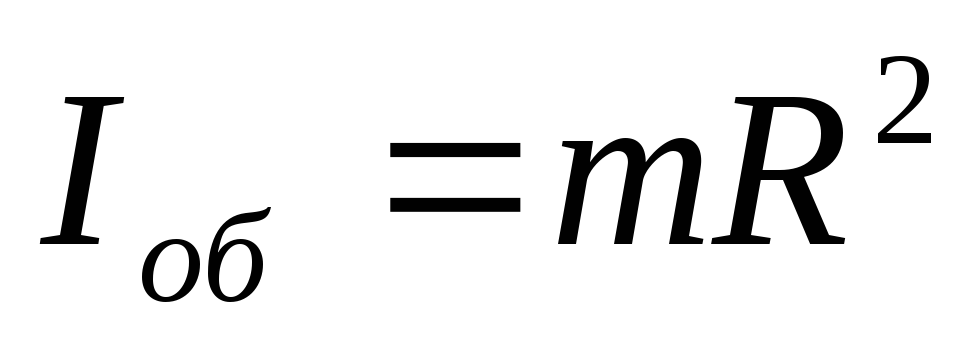
где
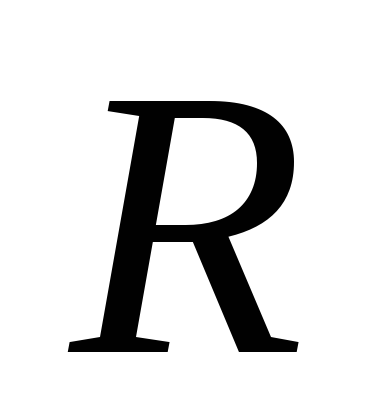
в) диска (сплошного цилиндра) относительно оси, перпендикулярной плоскости диска и проходящей через его центр тяжести (совпадающей с осью цилиндра )
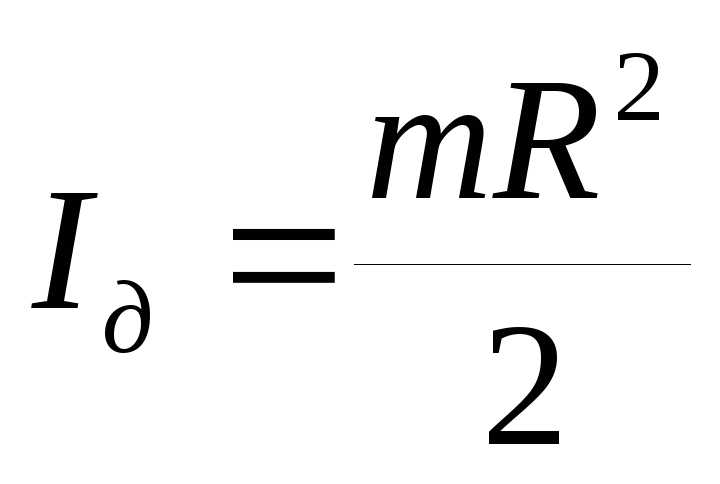
где
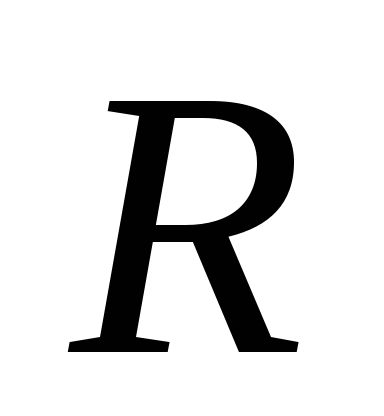
г) шара радиуса R относительно оси произвольного направления, проходящей через его центр тяжести
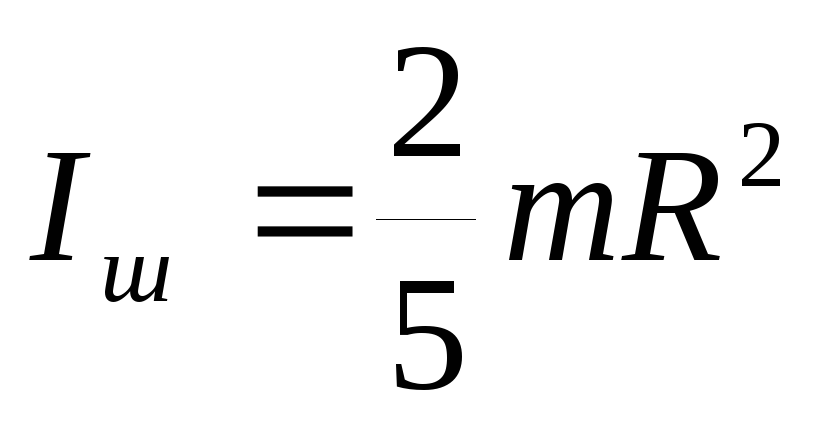
Момент инерции тела зависит: 1) от формы и размеров тела, 2) от массы и распределения масс, 3) от положения оси относительно тела.
Теорема Штейнера о параллельных осях записывается как:
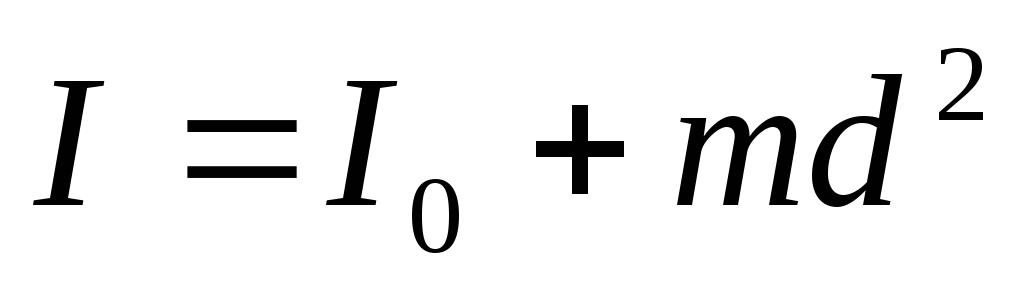
где
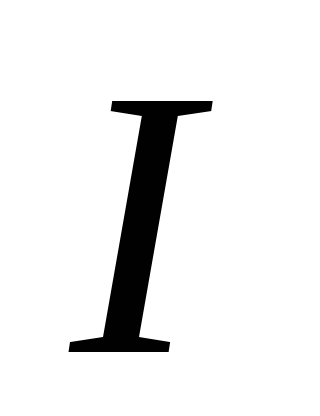 m
m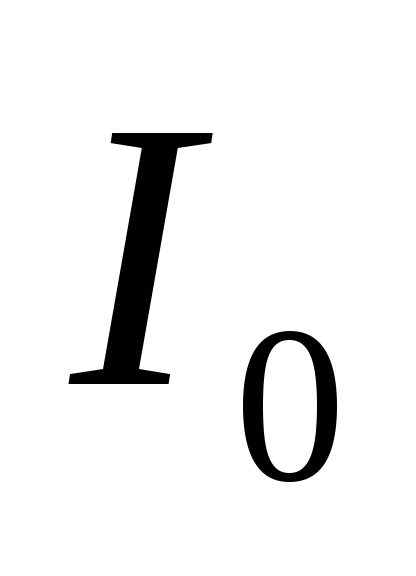

Маятник Обербека представляет собой крестовину, состоящую из шкива и четырех равноплечих стержней, закрепленных на горизонтальной оси (см. рис.2). На стержнях на равных расстояниях от оси вращения
 mm1hm1
mm1hm1
Запишем второй закон Ньютона для падающего груза в векторной форме
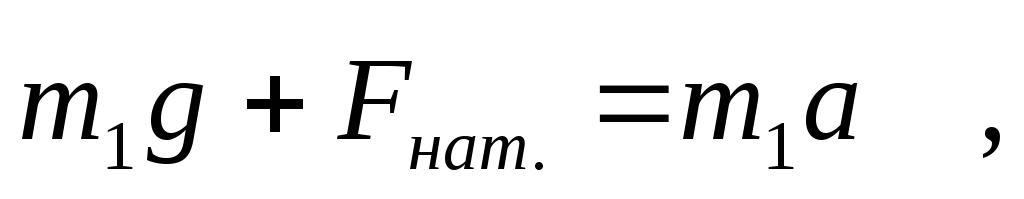
где
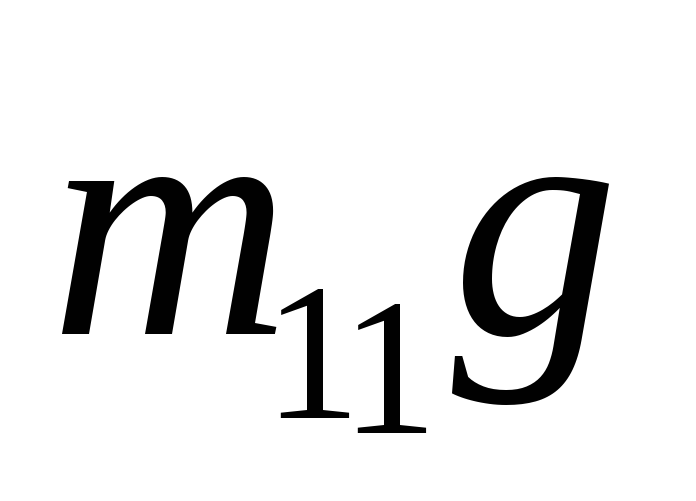
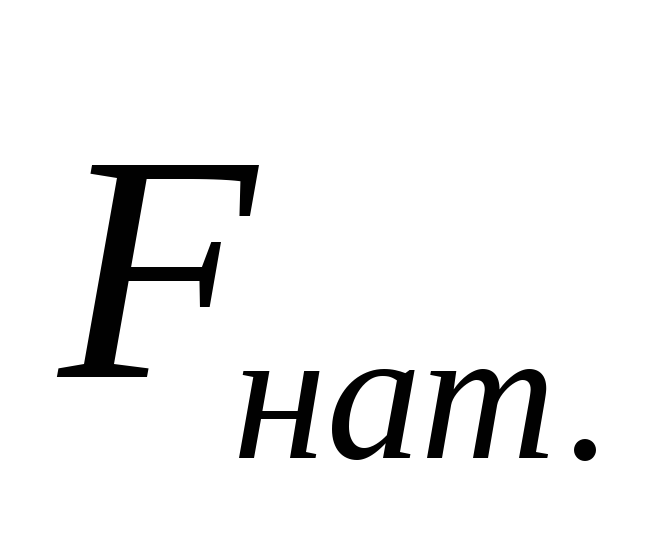
 m1
m1
Принимая направление движения груза за положительное, перепишем уравнение (I) в скалярной форме
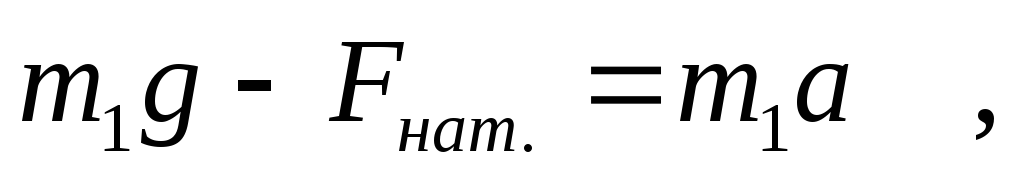
откуда получим выражение для силы натяжения шнура
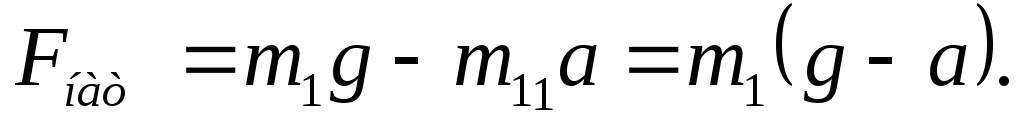
Линейное ускорение a находится из формулы пути равноускоренного движения без начальной скорости
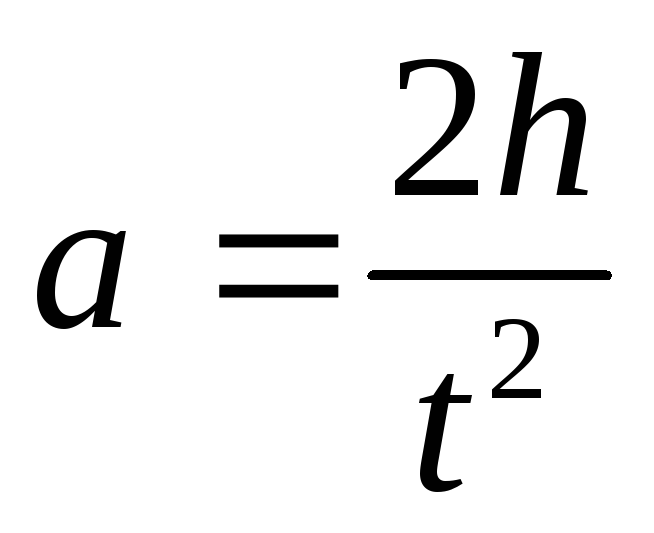
где h – высота падения груза m1; t – время падения.
Сила натяжения нити Fнат вызывает ускоренное вращение крестовины. Основной закон вращательного движения крестовины с учетом сил трения запишется так :
где М – момент силы натяжения; Mтр — момент сил трения; I — момент инерции крестовины; i — угловое ускорение, с которым вращается крестовина. Величина момента сил трения Mтр по сравнению с величиной вращающего момента М невелика, и, следовательно, ею можно пренебречь.
Из уравнения ( 5 ) с учетом сделанного замечания получаем оконча-тельную формулу для расчета момента инерции крестовины
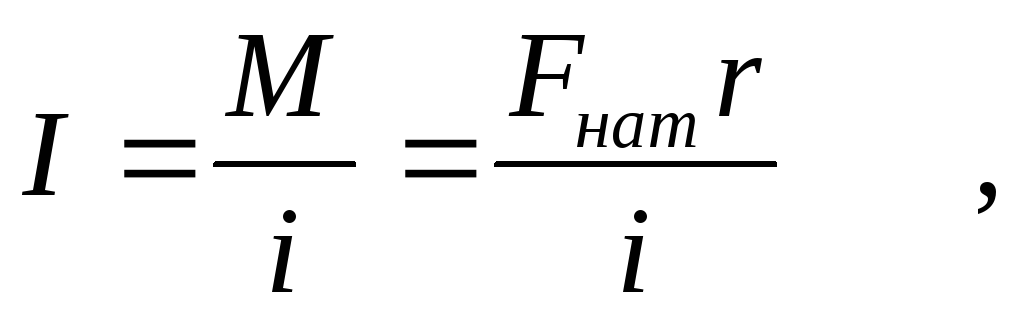
где r — радиус шкива. Угловое ускорение i определяется по формуле
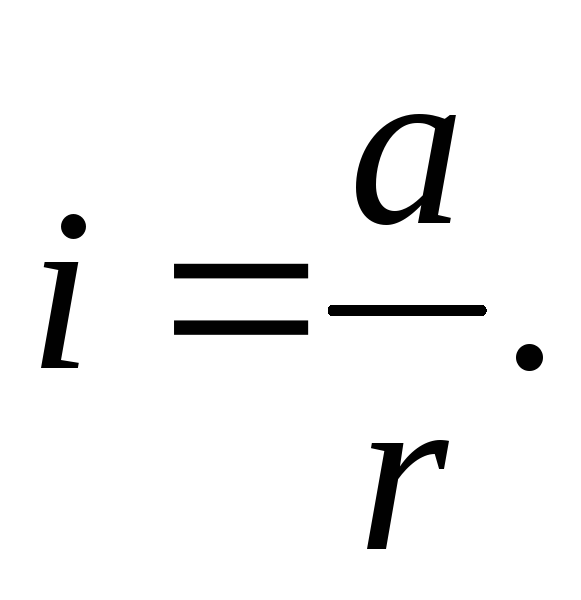
Подставляя (3) и (7) в (6), получаем окончательную формулу для расчета момента инерции крестовины
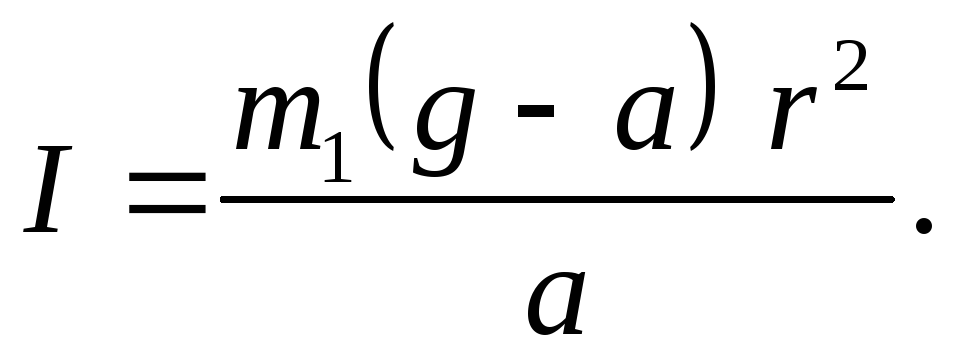
Порядок выполнения работы.
Экспериментальное определение момента инерции системы 4 х грузов.
1. Снять со стержней грузы m .
2. Намотать в один слой шнур на шкив, установив груз m1 на заранее выбран-ной высоте h. Отпустив крестовину, замерить время падения tо груза с помо-щью секундомера. Опыт повторить пять раз (при одной и той же высоте паде-ния h ).
3. Закрепить на концах стержней грузы m.
4. Выполнить операции, указанные в пункте 2, измеряя секундомером время падения t. Опыт повторить пять раз.
5. С помощью штангенциркуля измерить диаметр шкива d в пяти разных положениях.
6. Результаты измерений занести в таблицу. Найти приближенные значения и по методу Стьюдента оценить абсолютные погрешности измерения величин tо, t и d.
7. По формуле (4) рассчитать величину линейного ускорения a, с которым падает груз m1 для случаев:
8. По формуле (8) вычислить момент инерции крестовины без грузов (Io) и с грузами (I), используя приближенные значения m1, R, g и полученные значения а и ао.
Вычислить погрешности измерений по формулам:
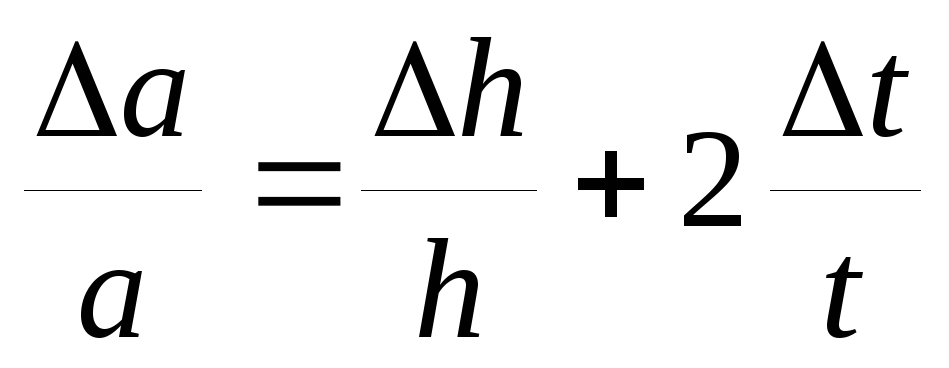
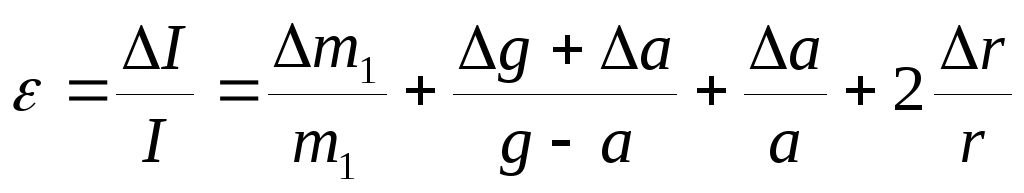
Устройство и принцип действия маятника Обербека
В работе используется крестообразный маятник Обербека (рис.7), который состоит из двух взаимно перпендикулярных стержней АВ и CD, ввинченных в шкив К. Крестовина может вращаться при падении груза Р, привязанного к нити, намотанной на шкив. По стержням АВ и CD могут перемещаться четыре груза, массы m которых одинаковы.
где R – расстояние от груза до оси вращения.
Если на шкив намотать нить и к ее концу прикрепить груз, то при его падении маятник будет вращаться с угловым ускорением e, а сам груз будет двигаться с линейным ускорением а. Вращающий момент будет равен произведению силы натяжения нити Fн на радиус шкива r: M = Fн r. Движение груза вниз происходит под действием двух сил: силы тяжести (F1= m1g или F2 = m2g), направленной вниз, и силы натяжения нити Fн, направленной вверх. Результирующая сила, сообщающая ускорение, будет равна
откуда сила натяжения Fн = m (g – a)
Момент этой силы относительно оси вращения
Если за время t груз упал с высоты h, то
откуда линейное ускорение
Формулу (5) можно записать в виде
а угловое ускорение



























