Изгиб

Перемещения при изгибе.

Под действием нагрузки при изгибе ось балки искривляется. При этом наблюдается растяжение волокон на выпуклой и сжатие — на вогнутой частях балки. Кроме того, происходит вертикальное перемещение центров тяжести поперечных сечений и их поворот относительно нейтральной оси. Для характеристики деформации при изгибе используют следующие понятия:

Прогиб балки Y — перемещение центра тяжести поперечного сечения балки в направлении, перпендикулярном к ее оси.

Прогиб считают положительным, если перемещение центра тяжести происходит вверх. Величина прогиба меняется по длине балки, т.е. y = y (z)

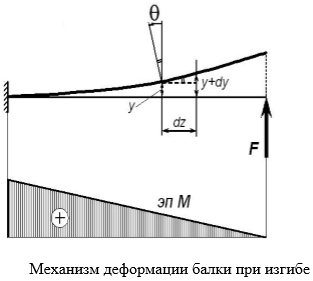
Угол поворота сечения — угол θ, на который каждое сечение поворачивается по отношению к своему первоначальному положению. Угол поворота считают положительным при повороте сечения против хода часовой стрелки. Величина угла поворота меняется по длине балки, являясь функцией θ = θ (z).

Самыми распространёнными способами определения перемещений является метод Мора и правило Верещагина.

Правило Верещагина.

Для случая, когда эпюра изгибающих моментов от заданной нагрузки
имеет произвольное, а от единичной нагрузки – прямолинейное очертание, удобно использовать графоаналитический способ, или правило Верещагина.

где A_f – площадь эпюры изгибающего момента М_f от заданной нагрузки; y_c – ордината эпюры от единичной нагрузки под центром тяжести эпюры М_f ; EI_x – жесткость сечения участка балки. Вычисления по этой формуле производятся по участкам, на каждом из которых прямолинейная эпюра должна быть без переломов. Величина (A_f*y_c) считается положительной, если обе эпюры располагаются по одну сторону от балки, отрицательной, если они располагаются по разные стороны. Положительный результат перемножения эпюр означает, что направление перемещения совпадает с направлением единичной силы (или момента). Сложная эпюра М_f должна быть разбита на простые фигуры(применяется так называемое «расслоение эпюры»), для каждой из которых легко определить ординату центра тяжести. При этом площадь каждой фигуры умножается на ординату под ее центром тяжести.

Дифференциальные зависимости Журавского.

Между интенсивностью q распределенной нагрузки, выражениями для поперечной силы Q и изгибающего момента М установлены дифференциальные зависимости:

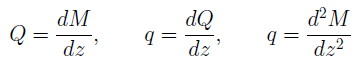
На основе этих зависимостей можно выделить следующие общие закономерности эпюр поперечных сил Q и изгибающих моментов М:

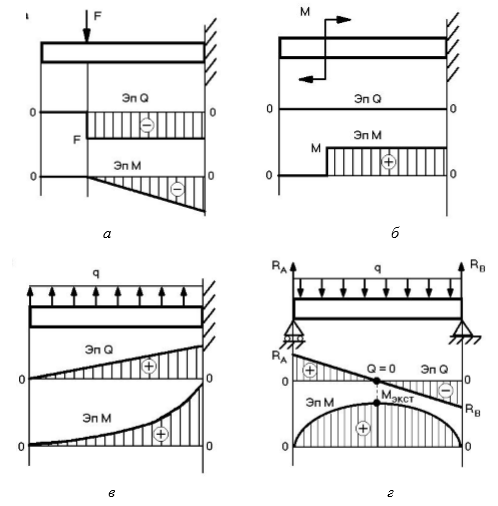
Особенности эпюр внутренних силовых факторов при изгибе.

1. На участке балки, где нет распределенной нагрузки, эпюра Q представлена прямой линией, параллельной базе эпюре, а эпюра М — наклонной прямой (рис. а).

2. В сечении, где приложена сосредоточенная сила, на эпюре Q должен быть скачок, равный значению этой силы, а на эпюре М —точка перелома (рис. а).

3. В сечении, где приложен сосредоточенный момент, значение Q не изменяется, а эпюра М имеет скачок, равный значению этого момента, (рис. 26, б).

4. На участке балки с распределенной нагрузкой интенсивности q эпюра Q изменяется по линейному закону, а эпюра М — по параболическому, причем выпуклость параболы направлена навстречу направлению распределенной нагрузки (рис. в, г).

5. Если в пределах характерного участка эпюра Q пересекает базу эпюры, то в сечении, где Q = 0, изгибающий момент имеет экстремальное значение M_max или M_min (рис. г).