Преобразования графиков функций с примерами решения и образцами выполнения

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).

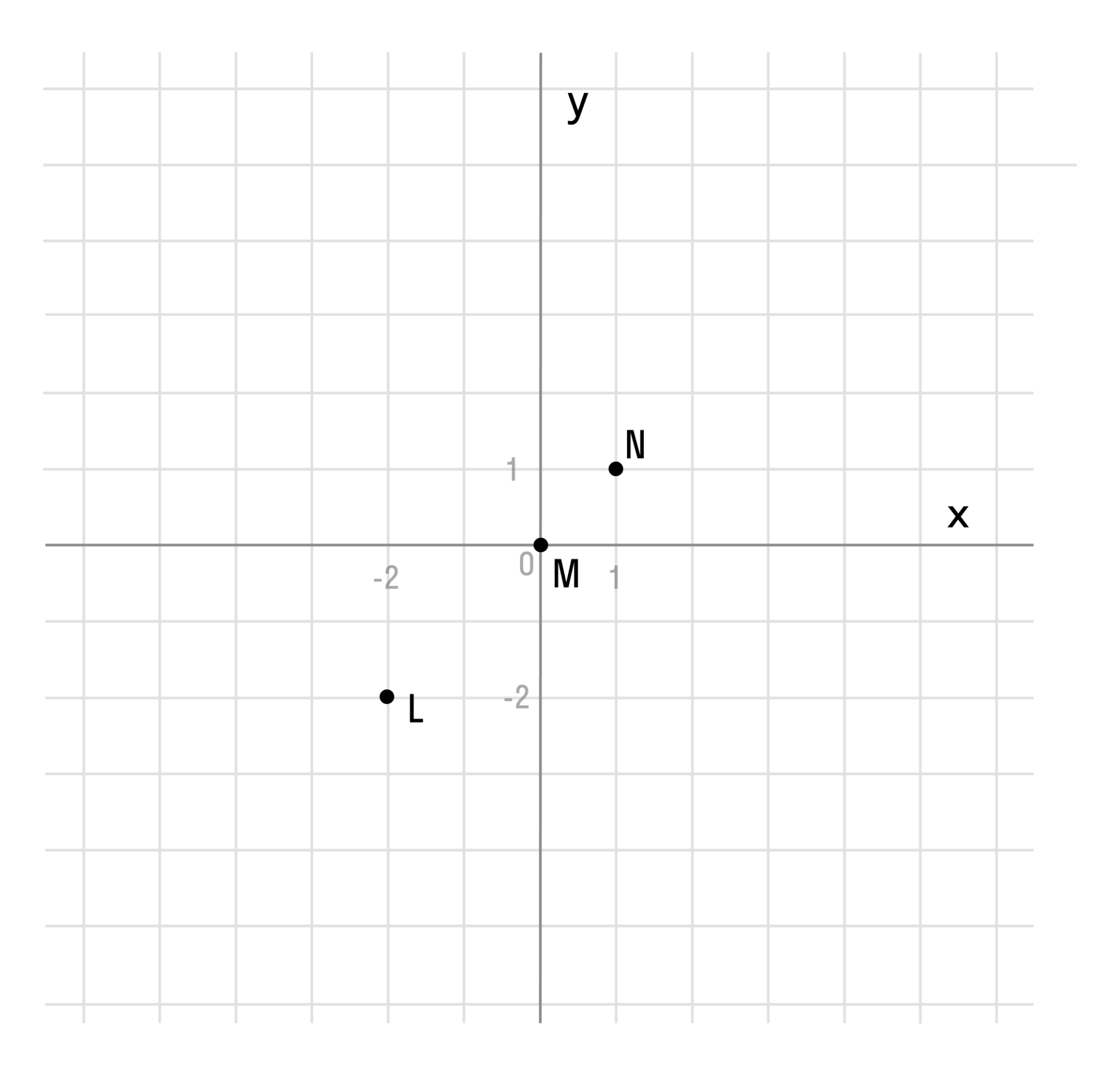
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

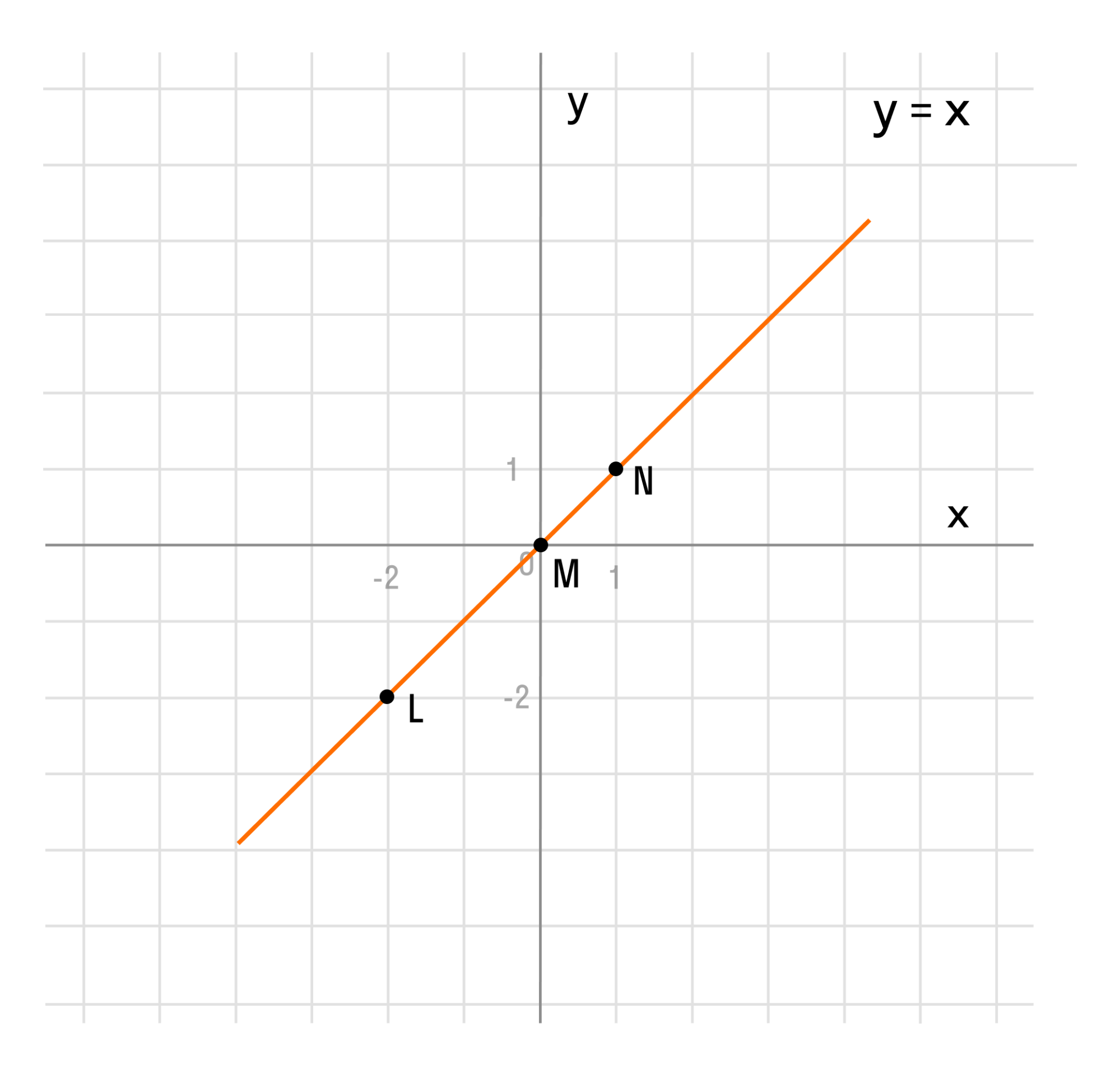
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться при решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика

Запоминаем!
Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.

Выберите идеального репетитора по математике
15 000+ проверенных преподавателей со средним рейтингом 4,8. Учтём ваш график и цель обучения
Выбрать!

Примеры

Функция	График функции	Описание
f(x)={−1,x<,x=1,x>{\displaystyle f(x)={\begin{cases}-1,&x<0\\0,&x=0\\1,&x>0\end{cases}}}		Функция y=sgn⁡(x).{\displaystyle y=\operatorname {sgn}(x).} В точке x=  y={\displaystyle x=0~~y=0.}
f(x)={,x=18,x=215,x=3{\displaystyle f(x)={\begin{cases}0,&x=1\\8,&x=2\\15,&x=3\end{cases}}}		Пример графика функции, определённой только в трёх точках {1,2,3}{\displaystyle \{1,2,3\}} и содержит только три точки с координатами (1,){\displaystyle (1,0)}, (2,8){\displaystyle (2,8)} и (3,15).{\displaystyle (3,15).}
f(x)=sin⁡(x){\displaystyle f(x)=\sin(x)}f(x)=cos⁡(x){\displaystyle f(x)=\cos(x)}f(x)=tg⁡(x){\displaystyle f(x)=\operatorname {tg} (x)}f(x)=ctg⁡(x){\displaystyle f(x)=\operatorname {ctg} (x)}f(x)=sec⁡(x){\displaystyle f(x)=\sec(x)}f(x)=cosec⁡(x){\displaystyle f(x)=\operatorname {cosec} (x)}		Графики тригонометрических функций: синуса, косинуса, тангенса, котангенса, секанса, косеканса
f(x)=1x{\displaystyle f(x)={\frac {1}{x}}}		График гиперболы. При x={\displaystyle x=0} претерпевает и в точке x={\displaystyle x=0} не определена.
f(x)=bx{\displaystyle f(x)=b^{x}}		Графики функций y=bx{\displaystyle y=b^{x}} различными основаниями b{\displaystyle b}: основание: 10 основание: e основание: 2 основание: 12 Каждая кривая проходит через точку (0, 1).
f(x)=x3−9x{\displaystyle f(x)=x^{3}-9x}		График f(x)=x3−9x{\displaystyle f(x)=x^{3}-9x} кубического многочлена вещественной переменной, это множество {(x,x3−9x)∈R2 |x∈R}{\displaystyle \{(x,x^{3}-9x)\in \mathbb {R} ^{2}\ |x\in \mathbb {R} \}}.

Преобразование графиков функций

В этой статье мы расскажем об основных преобразованиях графиков функций. Что нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали. Как задать растяжение графика по горизонтали или вертикали. Как отразить график относительно оси Х или Y.

Очень жаль, что эта тема — полезная и очень интересная — выпадает из школьной программы. На нее не постоянно хватает времени. Из-за этого многим старшеклассникам не даются задачи с параметрами — которые на самом деле похожи на конструктор, где вы собираете решение из знакомых элементов. Хотя бы для того, чтобы решать задачи с параметрами, стоит научиться строить графики функций.

Но конечно, не только для того, чтобы сдать ЕГЭ. Первая лекция на первом курсе технического или экономического вуза посвящена функциям и графикам. Первые зачеты в курсе матанализа связаны с функциями и графиками.

Начнем со сдвигов графиков по Х и по Y.

Сдвиг по горизонтали.

Пусть функция задана формулой и Тогда график функции сдвинут относительно исходной на а вправо. График функции сдвинут относительно исходной на а влево.

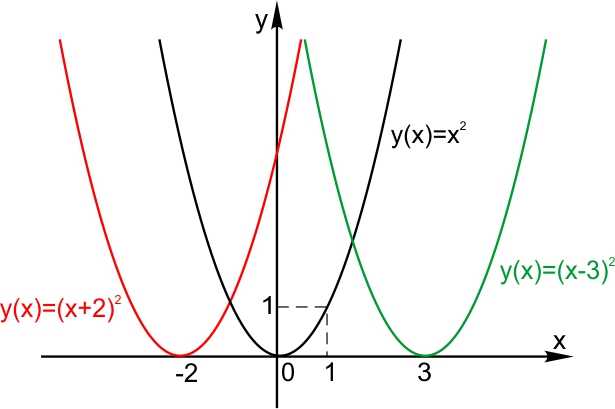
1. Сдвиг по вертикали.

Пусть функция задана формулой и С — некоторое положительное число. Тогда график функции сдвинут относительно исходного на С вверх. График функции сдвинут относительно исходного на С вниз.

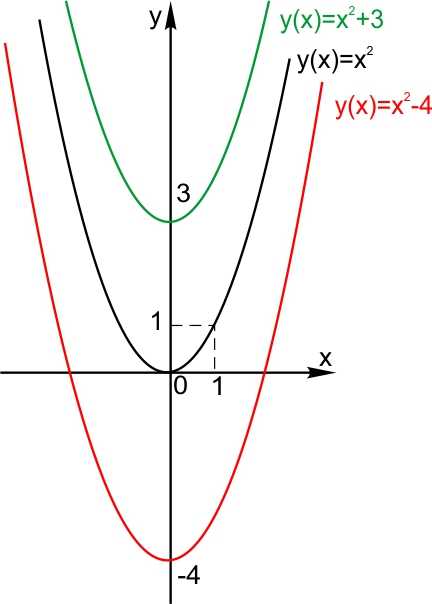
Теперь растяжение графика. Или сжатие.

2. Растяжение (сжатие) по горизонтали.

Пусть функция задана формулой и Тогда график функции растянут относительно исходного в k раз по горизонтали, если , и сжат относительно исходного в k раз по горизонтали, если

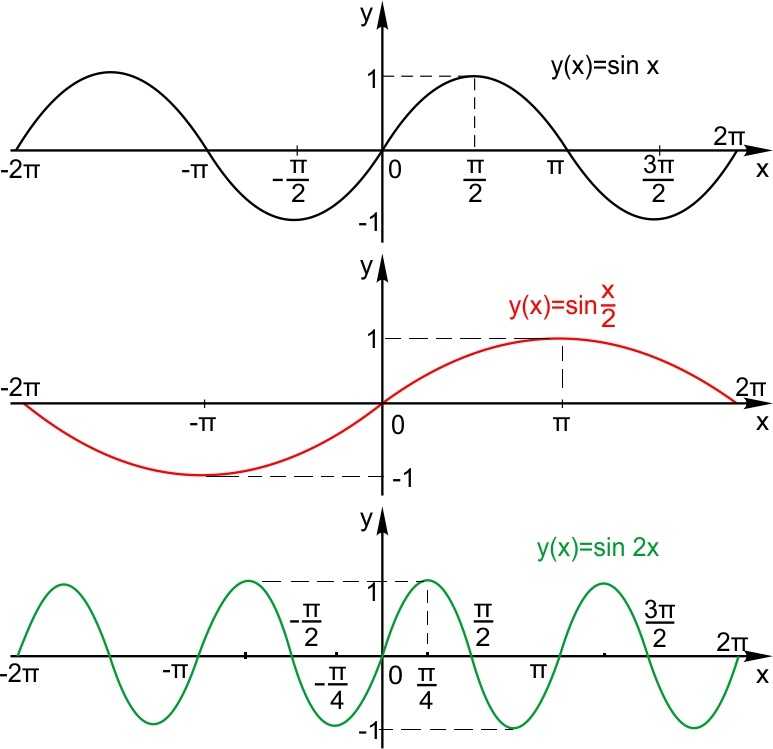
3. Растяжение (сжатие) по вертикали

Пусть функция задана формулой и Тогда график функции растянут относительно исходного в М раз по вертикали, если , и сжат относительно исходного в М раз по вертикали, если

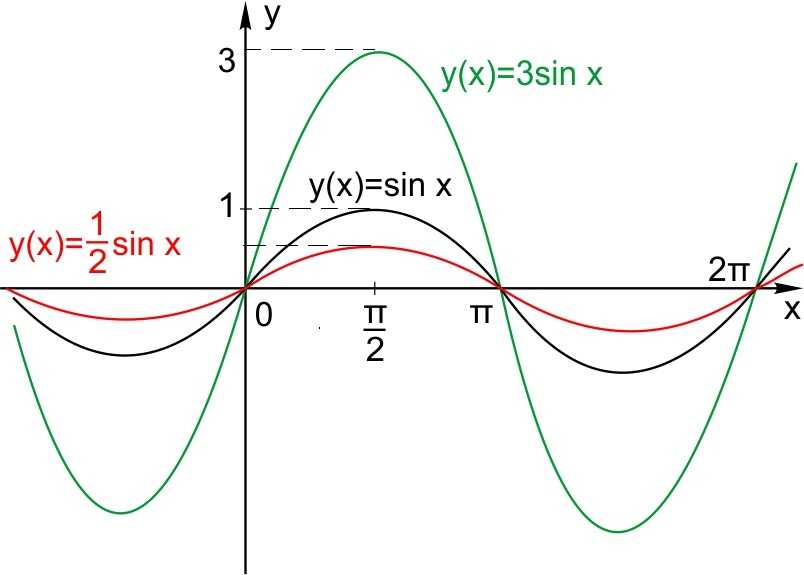
И отражение по горизонтали.

4. Отражение по горизонтали

График функции симметричен графику функции относительно оси Y.

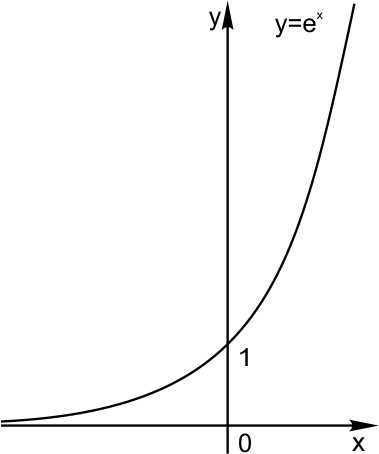
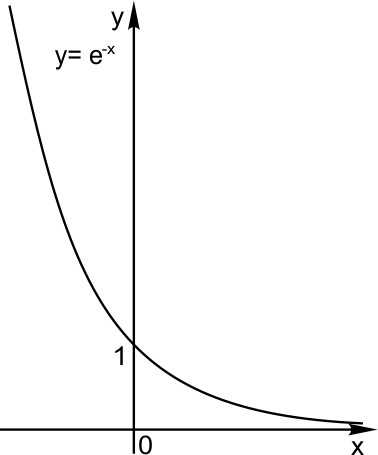
5. Отражение по вертикали.

График функции симметричен графику функции относительно оси Х.

Друзья, не возникло ли у вас ощущения, что вы все это где-то видели? Да, наверняка видели, если когда-либо редактировали изображения в графическом редакторе на компьютере. Изображение можно сдвинуть (по горизонтали или вертикали). Растянуть (по горизонтали или вертикали). Отразить. И все это мы делаем с графиками функций.

И еще два интересных преобразования. Здесь в формулах присутствует знак модуля. Если не помните, что такое модуль, — срочно повторите эту тему.

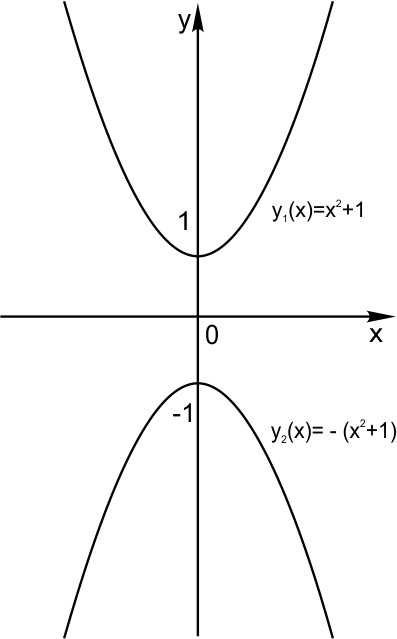
6. Графики функций и

На рисунке изображен график функции Она специально взята такая — несимметричная относительно нуля.

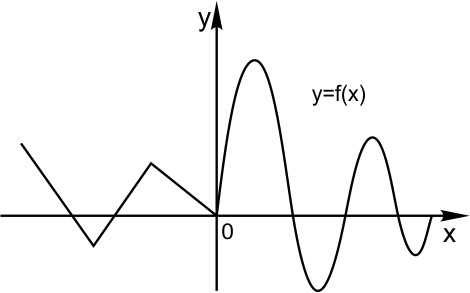
Построим график функции

Конечно же, мы пользуемся определением модуля.

Это мы и видим на графике. Для неотрицательных значений х график остался таким же, как был. А вместо каждого отрицательного х мы взяли противоположное ему положительное число. И поэтому вся та часть графика функции, что лежала слева от оси Х, заменилась на зеркально отраженную правую часть графика.

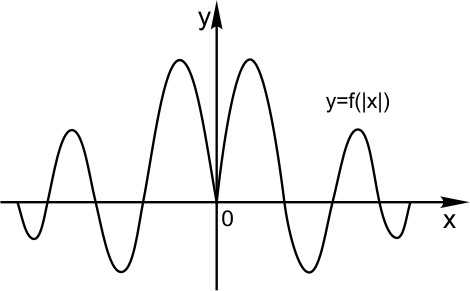
Теперь график функции Вы уже догадались, что будет. Вся часть графика, лежащая ниже оси Х, зеркально отражается в верхнюю полуплоскость. А верхняя часть графика, лежащая выше оси Х, остается на месте.

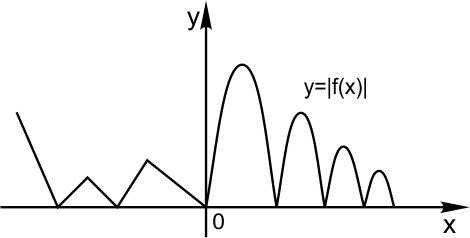
Как определить по формуле функции, будет график преобразован по горизонтали (по Х) или по вертикали (по Y)? Разница очевидна. Если сначала мы что-либо делаем с аргументом х (прибавляем к нему какое-либо число, умножаем на какое-либо число или берем модуль) — преобразование по Х. Если сначала мы нашли функцию, а затем уже к значению функции что-то прибавили, или на какое-нибудь число умножили, или взяли модуль, — преобразование по Y.

Вот самые простые задачи на преобразование графиков.

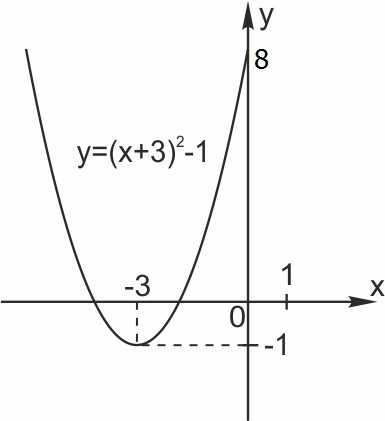
1. Построим график функции

Это квадратичная парабола, сдвинутая на 3 влево по x и на 1 вниз по y.

Вершина в точке

2. Построим график функции

Выделим полный квадрат в формуле.

График — квадратичная парабола, сдвинутая на 2 вправо по x и на 5 вниз по y.

Обратите внимание: график функции пересекает ось y в точке На нашем графике это точка

Презентация на тему: » Преобразование графика тригонометрической функции у = sin x путем сжатия и расширения ГБПОУ «Российский колледж традиционной культуры» Попова Л.А.» — Транскрипт:

1

Преобразование графика тригонометрической функции у = sin x путем сжатия и расширения ГБПОУ «Российский колледж традиционной культуры» Попова Л.А.

2

Цели : 1)Повторить правила преобразований функции: y = f (x) + m y = f (x + t) y = к f (x) y = f (к x) 2) Научиться строить графики вида y = f (x + t) + m 3)Закрепить умения, выполнив практические задания

3

Алгоритм построения графиков График функции y = sin (x-a) можно получить параллельным переносом графика функции y = sinx вдоль оси Ох на а единиц вправо. График функции y = sin (x+a) можно получить параллельным переносом графика функции y = sinx вдоль оси Ох на а единиц влево.

4

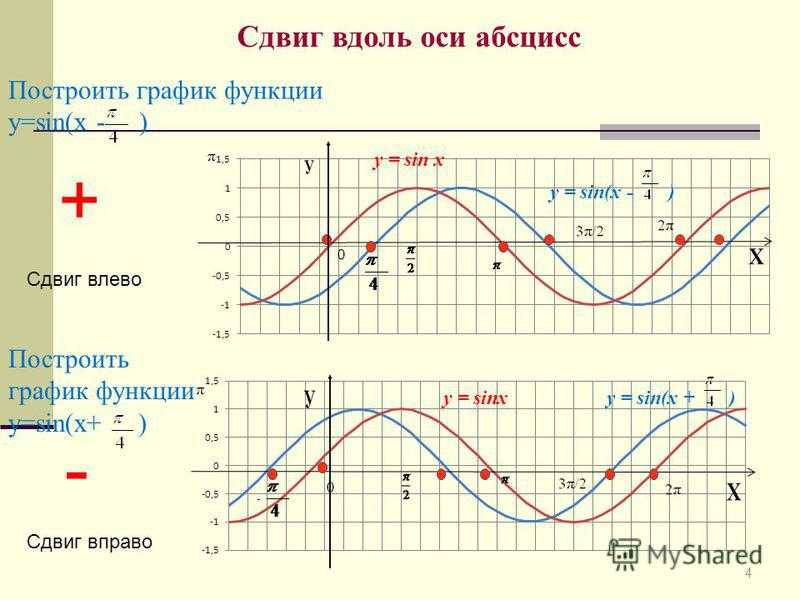
4 Сдвиг вдоль оси абсцисс Построить график функции у=sin(х — ) Построить график функции у=sin(х+ ) + Сдвиг влево — Сдвиг вправо y = sin x y = sin(x — ) y = sin(x + )y = sinx

5

Задание: Постройте в одной координатной плоскости графики функций: y 1 = sinx; у 2 = sin(x + ); у 3 = sin(x ).

6

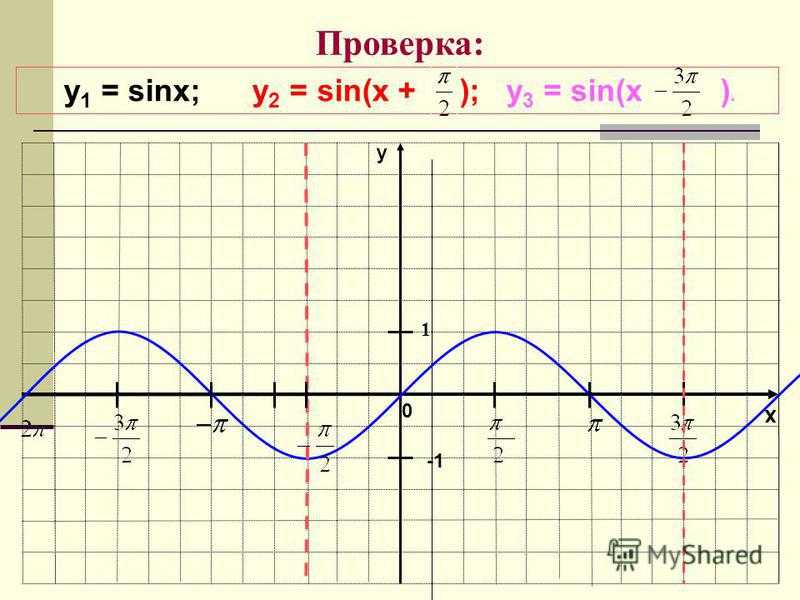
x y 1 Проверка: y 1 = sinx; у 2 = sin(x + ); у 3 = sin(x ). 0

7

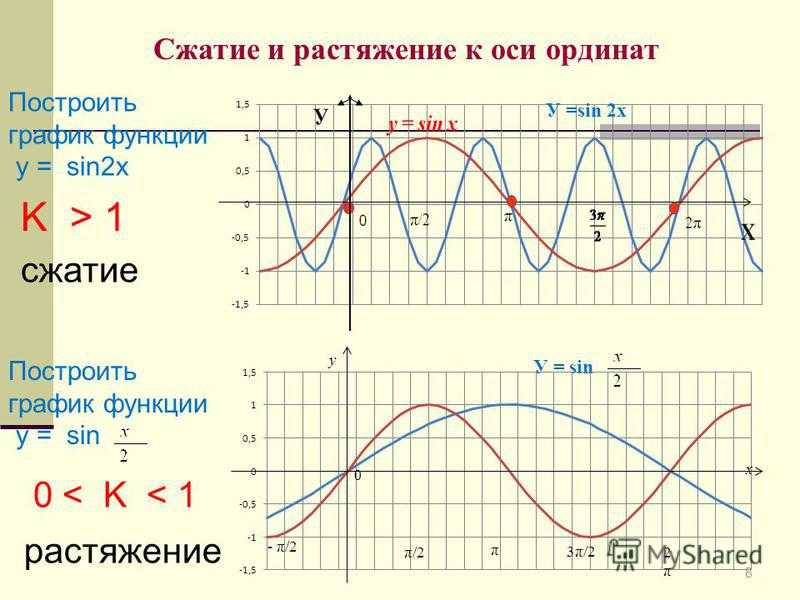
Алгоритм построения графиков График функции y = sin (Кx) (К>0) можно получить из графика функции y = sin x его растяжением (при 00) можно получить из графика функции y = sinx его сжатием (при К>1 сжатием в К раз) вдоль оси Ох.

8

8 Сжатие и растяжение к оси ординат Построить график функции у = sin2 х Построить график функции у = sin K > 1 сжатие 0

9

Алгоритм построения графиков: График функции y = Кsin (x) (К>0) можно получить из графика функции y = sin x его растяжением (при К>1 растяжением в К раз) вдоль оси Оу. График функции y = Кsin (x) (К>0) можно получить из графика функции y = sinx его сжатием (при 0

10

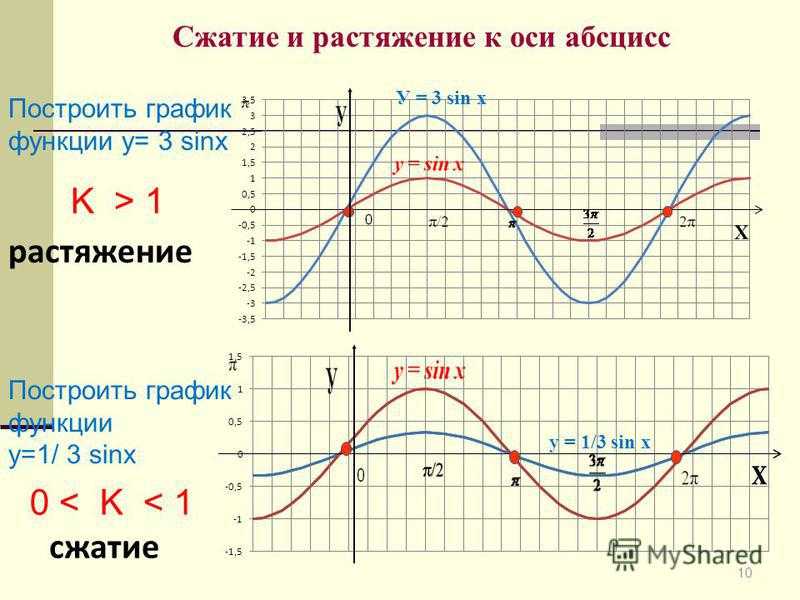
10 Сжатие и растяжение к оси абсцисс K > 1 растяжение 0

11

Постройте в одной координатной плоскости графики функций : y 1 = sinx; у 2 = 2sinx у 3 = ¼ sinx Задание:

12

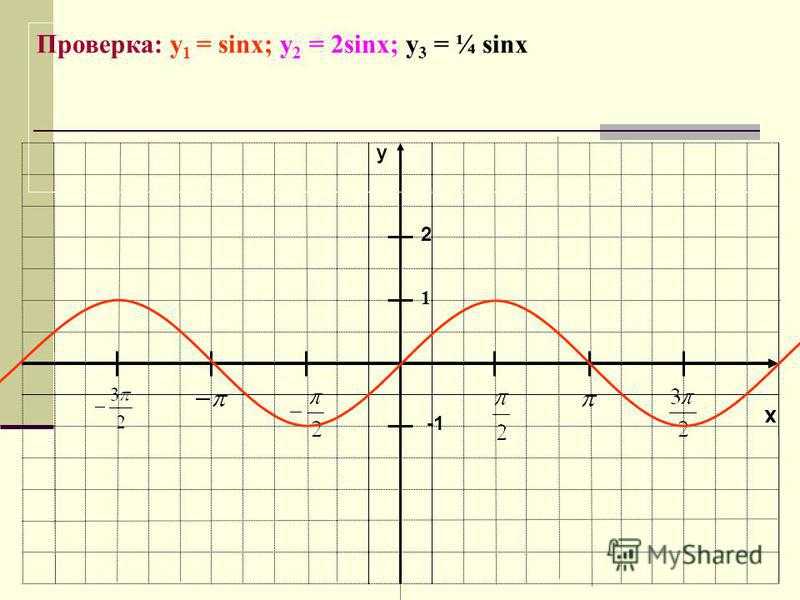
x y 1 Проверка: y 1 = sinx; у 2 = 2sinx; у 3 = ¼ sinx 2

13

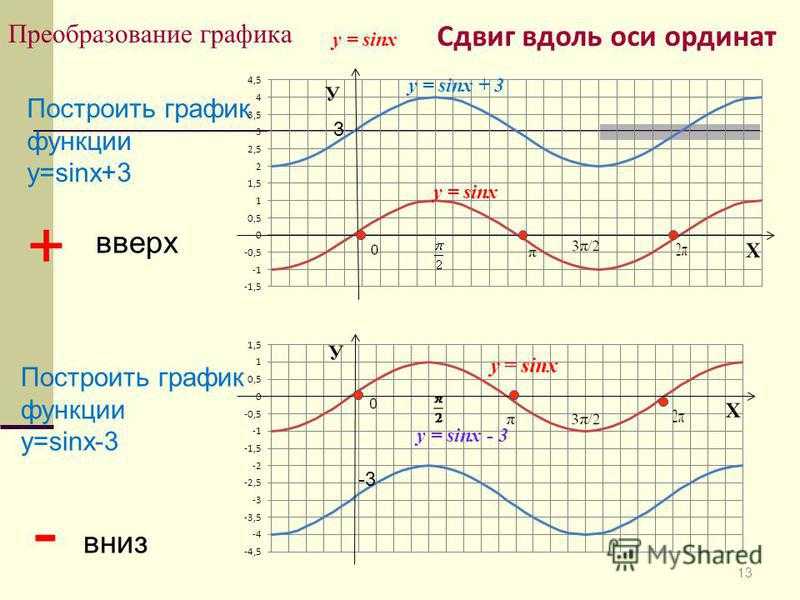
13 Сдвиг вдоль оси ординат Построить график функции у=sins+3 Построить график функции у=sins-3 + вверх — вниз y = sinx y = sinx + 3 y = sinx y = sinx Преобразование графика

14

Задание: Постройте в одной координатной плоскости графики функций: y1 = sinx; у 2 = sinx + 2; у 3 = sinx — 2.

15

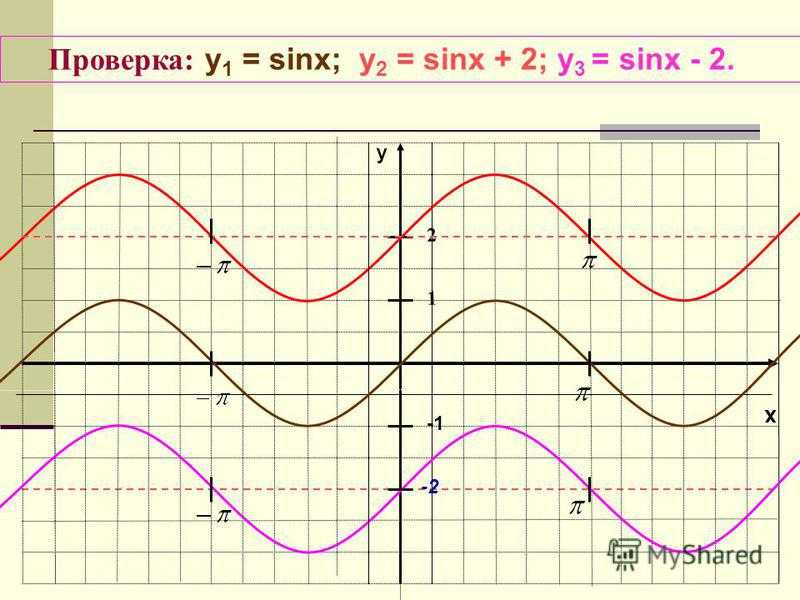
x y 1 -2 Проверка: y 1 = sinx; у 2 = sinx + 2; у 3 = sinx

16

Алгоритм построения графиков: График функции y = sin (x) + в можно получить параллельным переносом графика функции y = sin x вдоль оси Оу на в единиц.

17

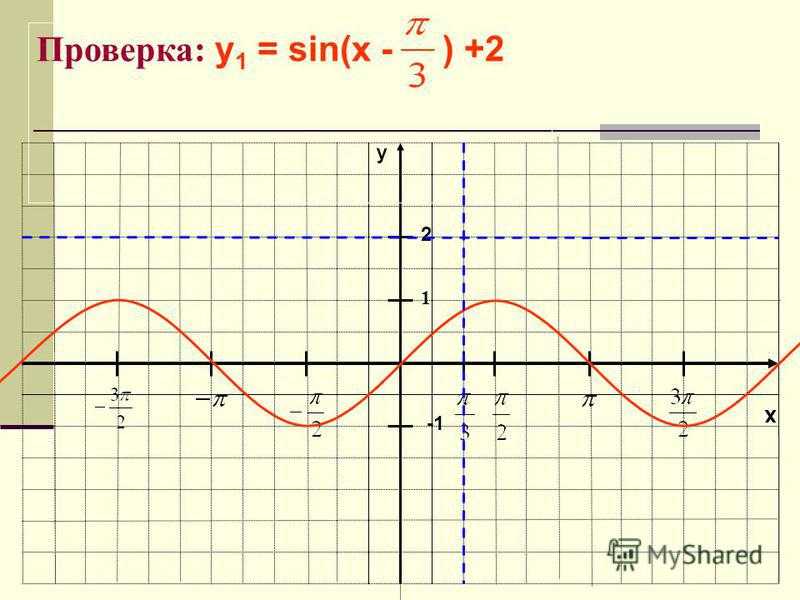
Постройть график функции: Задание: у 1 = sin(x — ) +2

18

x y 1 Проверка: у 1 = sin(x — ) +2 2

19

Вывод: График функции y=f(x + t) + m может быть получен из графика функции y=f(x) с помощью двух последовательных сдвигов на t единиц вдоль оси Ох и на m единиц вдоль оси Оу.

20

Постройте самостоятельно графики функций: Вариант 1. Вариант у = sin(x– п/3); 1. y=sin(x — п/4); 2. у = six+3,5; 2. y=sinx – 1,5; 3. у = 4sinx 3. у = 1/3sinx 4. у =sin(x – п/4)+3; 4. y=sin(x — п/3)-2; 5. у = ¼sin(x – п/4)-1; 5. y=2sin(x+п/2)-1;

21

Спасибо за урок

Определение графика

При рассмотрении отображения произвольного вида fX→Y{\displaystyle f:X\to Y}, действующего из множества X{\displaystyle X} в множество Y{\displaystyle Y}, графиком функции называется следующее множество упорядоченных пар:

Γf={(x,f(x))∈X×Y∣x∈X}.{\displaystyle \Gamma _{f}=\{\,(x,f(x))\in X\times Y\mid x\in X\,\}.}

В частности, при рассмотрении динамических систем, изображающая точка (t,f(t)){\displaystyle (t,f(t))} представляет собою график решения соответствующего дифференциального уравнения с заданными начальными условиями такой график часто называют фазовой траекторией системы.

График линейной функции

Линейная функция задается уравнением . График линейной функций представляет собой прямую. Для того, чтобы построить прямую достаточно знать две точки.

Пример 1

Построить график функции . Найдем две точки. В качестве одной из точек выгодно выбрать ноль.

Если , то

Берем еще какую-нибудь точку, например, 1.

Если , то

При оформлении заданий координаты точек обычно сводятся в таблицу:

 
А сами значения рассчитываются устно или на черновике, калькуляторе.

Две точки найдены, выполним чертеж:

При оформлении чертежа всегда подписываем графики.

Не лишним будет вспомнить частные случаи линейной функции:

Обратите внимание, как я расположил подписи, подписи не должны допускать разночтений при изучении чертежа. В данном случае крайне нежелательно было поставить подпись рядом с точкой пересечения прямых  ,  или справа внизу между графиками. 1) Линейная функция вида  () называется прямой пропорциональностью

Например,. График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается – достаточно найти всего одну точку

1) Линейная функция вида  () называется прямой пропорциональностью. Например, . График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается – достаточно найти всего одну точку.

2) Уравнение вида  задает прямую, параллельную оси , в частности, сама ось  задается уравнением . График функции строится сразу, без нахождения всяких точек. То есть, запись  следует понимать так: «игрек всегда равен –4, при любом значении икс».

3) Уравнение вида  задает прямую, параллельную оси , в частности, сама ось  задается уравнением . График функции также строится сразу. Запись  следует понимать так: «икс всегда, при любом значении игрек, равен 1».

Некоторые спросят, ну зачем вспоминать 6 класс?! Так-то оно, может и так, только за годы практики я встретил добрый десяток студентов, которых ставила в тупик задача построения графика вроде  или .

Построение прямой – самое распространенное действие при выполнении чертежей.

Прямая линия детально рассматривается в курсе аналитической геометрии, и желающие могут обратиться к статье Уравнение прямой на плоскости.

Исследование функции

Важные точки графика функции y = f(x):

• стационарные и критические точки;

• точки экстремума;

• нули функции;

• точки разрыва функции.

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых значение функции равно нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

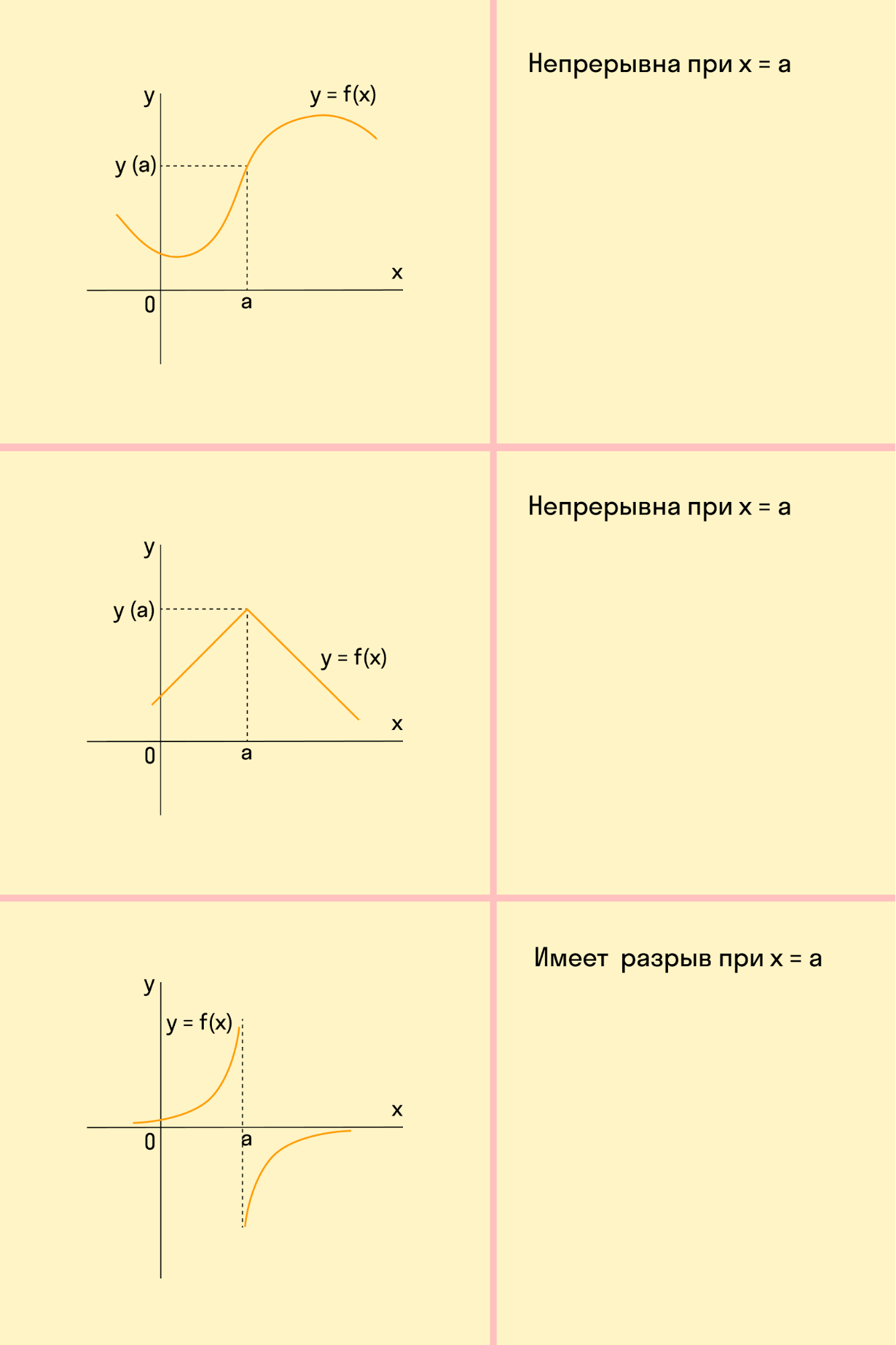
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

1. Найти область определения функции.

2. Найти область допустимых значений функции.

3. Проверить не является ли функция четной или нечетной.

4. Проверить не является ли функция периодической.

5. Найти точку пересечения с осью OY (если она есть).

6. Вычислить производную и найти критические точки, определить промежутки возрастания и убывания.

7. Промежутки знакопостоянства.

8. Асимптоты.

9. На основании проведенного исследования построить график функции.

У нас есть отличные курсы по математике для учеников с 1 по 11 классы!

Понятие функции

Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие значения функции. Вот, какими способами ее можно задать:

• Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.

• Графический способ — наглядно.

• Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.

• Словесный способ.

Область определения функции — это множество всех допустимых значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.

Например, для функции вида область определения выглядит так

х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): (-∞; 0) ⋃ (0; +∞).

Область значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): [0; +∞).

Графики функций с модулем

Для качественного усвоения материала необходимо понимать, что такое модуль. Краткую информацию о нём можно найти на странице Математические формулы и таблицы в справочном материале Горячие формулы школьного курса математики.

Применение модуля тоже представляет собой геометрическое преобразование графика. Не буду создавать сверхподробный мануал, отмечу только те моменты, которые, с моей точки зрения, реально пригодятся для решения других задач по вышке.

Сначала посмотрим, что происходит, когда модуль применяется к АРГУМЕНТУ функции.

Правило: график функции  получается из графика функции  следующим образом: при  график функции  сохраняется, а при  «сохранённая часть» отображается симметрично относительно оси .

Пример 22

Построить график функции

И снова вечная картина: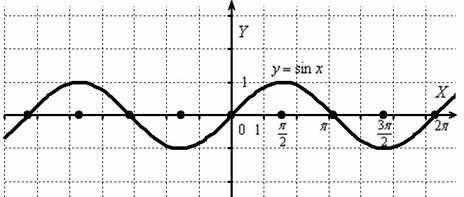
Согласно правилу, при  график сохраняется: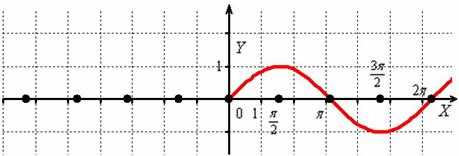
И сохранившаяся часть отображается симметрично относительно оси   в левую полуплоскость: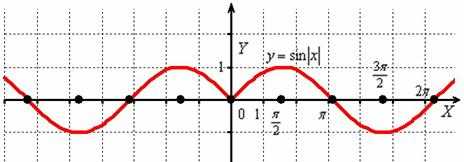

Действительно, функция  – чётная, и её график симметричен относительно оси ординат. Поясню детальнее смысл симметрии. Посмотрим на два противоположных значения аргумента, например, на  и . А какая разница? Модуль всё равно уничтожит знак «минус»: , то есть значения функции будут располагаться на одной высоте.

Функцию от модуля можно расписать в так называемом кусочном виде по следующему правилу: . В данном случае:

То есть, правая волна графика  задаётся функцией , а левая волна – функцией  (см. Пример 13).

Пример 23

Построить график функции

Аналогично, ветвь «обычной» экспоненты  правой полуплоскости отображаем симметрично относительно оси  в левую полуплоскость:
Распишем функцию в кусочном виде: , то есть правая ветвь задаётся графиком функции , а левая ветвь графиком .

Модуль не имеет смысл «навешивать» на аргумент чётной функции:  и т.п. (проанализируйте, почему).

И, наконец, завершим статью весёлой нотой – применим модуль к САМОЙ ФУНКЦИИ.

Правило: график функции  получается из графика функции  следующим образом: часть графика , лежащая НАД осью  сохраняется, а часть графика , лежащая ПОД осью  отображается симметрично относительно данной оси.

Странно, что широко известный график модуля «икс» оказался на 24-й позиции, но факт остаётся фактом =)

Пример 24

Построить график функции

Сначала начертим прямую, известную широкому кругу лиц: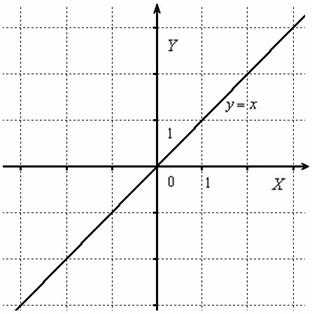
Часть графика, которая ВЫШЕ оси , остаётся неизменной, а часть графика, которая НИЖЕ оси  – отображается симметрично в верхнюю полуплоскость: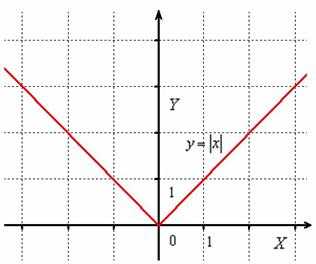

Модуль функции также раскрывается аналитически в кусочном виде:

Внимание! Формула отличается от формулы предыдущего пункта!

В данном случае: , действительно, правый луч задаётся уравнением , а левый луч – уравнением .

Кстати,  – редкий экземпляр, когда можно считать, что модуль применён, как к аргументу: , так и  к самой функции: . Изучим более «жизненную» ситуацию:

Пример 25

Построить график функции

Сначала изобразим график линейной функции :
То, что ВЫШЕ оси абсцисс – не трогаем, а то, что НИЖЕ – отобразим симметрично относительно оси  в верхнюю полуплоскость:

Согласно формуле , распишем функцию аналитически в кусочном виде: .

Или, упрощая оба этажа: , то есть правый луч задаётся функцией , а левый луч – функцией . Сомневающиеся могут взять несколько значений «икс», выполнить подстановку и свериться с графиком.

На какие функции модуль «не действует»? Модуль бессмысленно применять к неотрицательным функциям. Например: . Экспоненциальная функция и так полностью лежит в верхней полуплоскости: .

Всё возвращается на круги своя, синусом начали, синусом и закончим. Как в старой доброй сказке:

Пример 26

Построить график функции .

Изобразим сами знаете что =)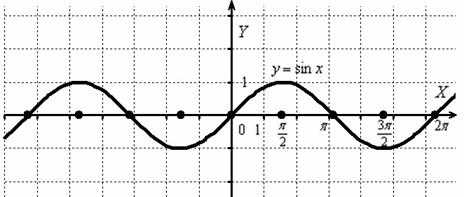

И снова – то, что находиться в верхней полуплоскости – оставим в покое, а содержимое подвала – отобразим симметрично относительно оси :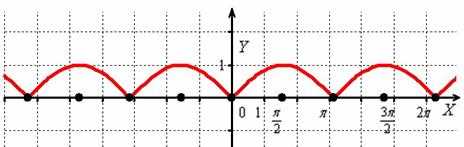

Кстати, понятен ли вам неформальный смысл такого симметричного отображения? Модуль «съедает» у  отрицательных чисел знак и делает их положительными, именно поэтому «подвальные» точки занимают противоположные места в верхней полуплоскости.

Распишем функцию в кусочном виде:

Решив два простейших школьных неравенства , получаем:, где  – любое целое число.

Да, статья была не самой приятной, но крайне необходимой. Однако повествование завершилось и стало немножко грустно =) Чем-то напомнило мне всё это урок про метод Симпсона, который тоже создавался в марте, и тоже достаточно долгое время. Наверное, громоздкие вещи пишутся по сезону =)

Желаю успехов!

(Переход на главную страницу)