Информатика

Введение

Потребность в счете возникла у людей с давних времен. Ученые археологи нашли много записей времен пещерного человека, с помощью которых они обозначали количество убитых животных, добытых шкур и собранного урожая. Так в 1937 году в Моравии была найдена кость с 55 зарубками. По мнению ученых они обозначали количество бизонов добытых вождем племени.

С развитием технологий, счет находил применение во всех областях социальной жизни человечества – астрономии, налогообложении и промышленности. Сейчас вычисления активно используются в информатике для представления информации в электронно-вычислительных машинах. В этой статье вы узнаете, что такое система исчисления, изучите основные определения, которые помогут вам лучше разобраться в теме, выясните, что такое позиционные и непозиционные системы исчисления и чем они отличаются.

Введение

На заре зарождения человеческого общества понятия счёта практически не существовало. Люди могли отличить два предмета от трёх, но всё что было больше этого скрывалось за термином «много». Как правило, при подсчёте чего-либо количество предметов соотносилось с количеством пальцев на конечностях.

Постепенный прогресс нашего общества сделал счёт насущной потребностью. Сначала изображение натуральных чисел сводилось к написанию чёрточек, но впоследствии для этих целей начали применяться буквенные обозначения и символы. Жители древнего Новгорода применяли славянский алфавит, для написания чисел над славянскими буквами ставили знак ~ (титло).

В Древнем Риме зародилась методика, которая известна и сегодня как римская система нумерации. В ней числовые значения представляются буквами латинского алфавита. Сегодня её используют для нумерации глав в книгах и тому подобного. Вот список римских цифр: I = 1; V = 5; X = 10; L = 50; С = 100; D = 500; M = 1000. В римской системе нумерации прослеживаются отголоски пятеричной системы счисления. Арифметические операции над большими числами в римской системе достаточно трудоёмки, но она применялась в Италии вплоть до тринадцатого века, а в некоторых европейских государствах аж до шестнадцатого века.

Славяне для обозначения чисел применяли весь алфавит, но с незначительными отклонениями от порядка следования букв в алфавите. Разные буквы обозначали разное число единиц, десятков и сотен. Такая система имела две существенные проблемы, которые и вызвали отказ от неё. Это слишком большое количество разных знаков, в частности для отображения большого числа, и, что ещё хуже, очень было неудобно выполнять арифметические операции.

Наиболее совершенной и доступной стала общеизвестная сегодня десятичная система счисления, которая зародилась в Индии, усовершенствована арабами и уже потом появилась в европейских странах. В качестве основания десятичной системы выбрано число десять. Конечно, существуют системы счисления, имеющие различные основания. Жители древнего Вавилона применяли шестидесятеричную систему счисления. Её отголоски видны и в наше время, поскольку мы и сегодня считаем, что в часе 60 минут, а в минуте 60 секунд. В древние времена люди так же пользовались двенадцатеричной системой. Сегодня от неё осталась широко известная «дюжина», то есть число двенадцать. Ещё существует обычай подсчитывать количество некоторых предметов не числом десятков, а числом дюжин, к примеру, это столовые приборы.

Арифметика для 2СС

Принципы выполнения простейших арифметических операций одинаковы для любых позиционных систем, независимо от основы:

Особенности арифметики СС с разными основами:

• при сложении чисел двух 1 в двоичной системе переполняется младший разряд (сумма = или ˃ основания СС), то единица переходит к большему разряду;
• если есть 0-1=1, идет заимствование из старшего разряда;
• умножать 2СС удобнее всего в столбик, учитывая 4 основные правила;
• заем единиц в 2СС при отнимании/делении, тогда она дает промежуточным разрядам по 1, а для занимаемого разряда сразу 11.

Примеры арифметических операций:

Для удобства разработаны готовые таблицы сложения в различных системах:

Сложение в 8-ой СС                                              в 16СС

С их помощью можно быстро суммировать в различных СС.

Сложение для разных СС на примере 15 и 6:

Если необходимо сложить числа из разных систем, их приводят к одной основе. Самым простым вариантом будет перевод в десятичную систему, решение простого примера и перевод результата в любую из систем.

Рассмотрим сумму 43₈ и 56₁₆. Результат можно выразить в любой СС, но проще привести к 8- или 16-ричной:

 Переводим число 56 в восьмеричную через двоичную:

Умножение в 8-ой СС

Непозиционные СС, их особенности

Первоначально древние люди ставили отметки (черточки-зарубки, точки), чтобы обозначить количество того или иного предмета. Отклики этого подхода все еще встречаются (полоски у военных, счетные палочки).

Постепенно от единиц они переходили к группам предметов по 3, 5, 10 единиц. Постепенно такие группы стали обозначаться определенными символами, что позволило сократить размер записи.

Римская СС

В ней определенным цифрам отвечают латинские буквы. Их сумма и будет числом.

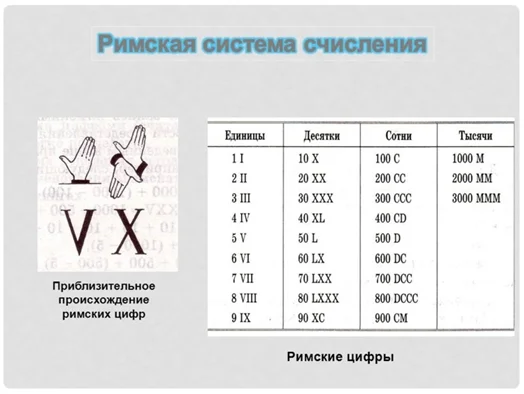
Основные рекомендации при пользовании римскими цифрами:

1. Символы следует писать по убыванию слева направо.
2. Нежелательно записывать подряд более 3 одинаковых знаков.
3. Положение цифры обозначает, какой ее вклад – отрицательный, если она стоит слева от большего числа, положительный – справа.

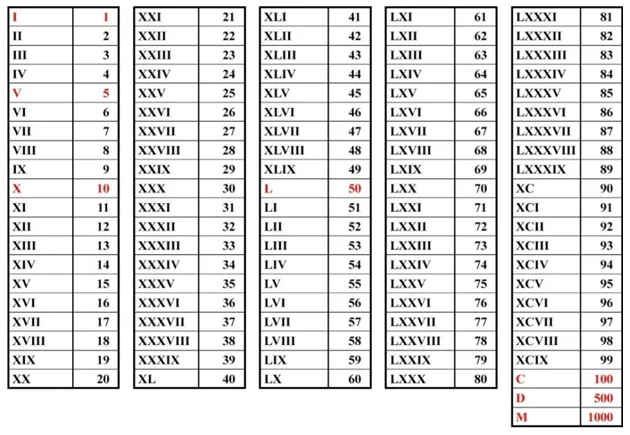Таблица римских цифр 

Недостаток этой СС в том, что для больших чисел недоступны операции сложения или другие, ещё она сложная и громоздкая. Зато римские цифры отлично вписались там, где нужна нумерация и эстетика: циферблаты, номера глав, списки, серии документов.

Аддитивные и мультипликативные системы счисления

Система счисления – понятие сложное, включающее в себя законы, по которым читаются и записываются числа, и по которым выполняются действия над ними

Для этого важно знать тип системы счисления. По типу различают аддитивную и мультипликативную системы счисления

Для аддитивной характерно то, что каждая цифра имеет свое значение, для прочтения числа необходимо сложить все значения используемых цифр. Например:

$XXXXVI = 10 + 10 + 10 + 10 + 5 + 1 = 46$

Для второго типа характерно то, что цифра может иметь различные значения в зависимости от ее местоположения в числе.

Рисунок 1.

(иероглифы по порядку: $2$, $1000$, $4$, $100$, $2$, $10$, $5$)

В этой записи два раза используется иероглиф $«2»$, и в каждом случае он принимает разные значения $«2000»$ и $«20»$.

$2\cdot 1000 + 4\cdot 100 + 2\cdot 10 + 5 = 2425$

Для аддитивной («добавительной») системы необходимо знать все цифры-символы и их значения (их бывает до 4-5 десятков), а также порядок записи. Например, в латинской записи если меньшая цифра записана перед большей, то производится вычитание, а если после, то сложение:

$IV = 5–1 = 4$

$VI = 5+1 = 6.$

Таблицы истинности

При помощи тех же нулей и единиц создаются таблицы истинности логических выражений, в которых описаны всевозможные варианты.

Основные логические операции

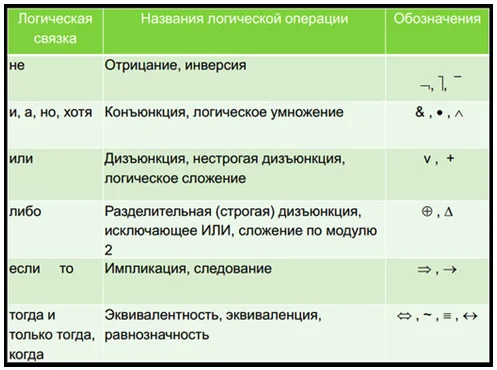
Например, конъюнкция является одной из логических операций. Она является истиной только в том случае, если два высказывания имеют истинные значения.

Логические переменные таблицы истинности обозначают p и q, а их значения выражают при помощи 0 и 1, где 0 – ложь, 1 – истина:

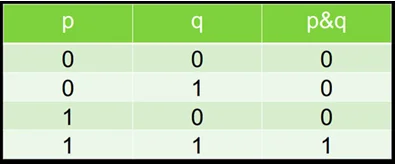
Фрагмент таблицы истинности для конъюнкции.

Так выражаются условия для всех логических операций.

Применяются таблицы истинности еще с начала 20 века в алгебре, логике, программировании.

Основные позиционные СС, правила перевода

Двоичная система счисления

Систему, на которой основывается работа компьютеров, придумал гениальный немецкий ученый Г.В. Лейбниц (еще до 19 века!). Он придумал и описал СС, в которой все вычисления проводятся при помощи двух простейших символов – 0 и 1.

Компьютер, как механическое устройство, получает команды в виде двоичной кодировки. Он не в силах понять сложные задания, человеческую речь, музыку или тысячи оттенков, а переводя/кодируя всю необходимую информацию при помощи 0 и 1 (сеть, отсутствие сети), можно передать ему любые команды или информацию. Естественно, такие задания выглядят как огромные массивы двух знаков.

Алгоритм перевода чисел из десятичной в двоичную систему:

1. Деление на основу СС до тех пор, пока не останется в остатке значение меньше значения основы.
2. Записать остатки, от последнего к первому.
3. Первый ноль можно не писать.

111 0100 1100₂ 

Этот порядок действия позволят переводить в любую позиционную СС. В данном случае, основа – 2, остаток < или равен =.

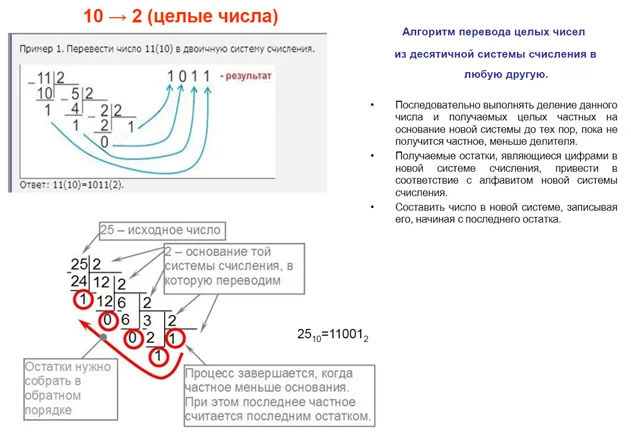
Обратный алгоритм перевода из двоичной в десятичную систему счисления:

Записать число развернуто, то есть, сколько сотен, десятков и единиц в нем, но учитывая основу – 2

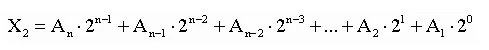
Объяснение. Развернутая форма записи 579: 5*102+7*101+9*10= 579₁₀.

Обычно мы пользуемся свернутой формой записи чисел, то есть без разбивки на разряды и умножения на основу.

1. Умножить и суммировать полученные значения.

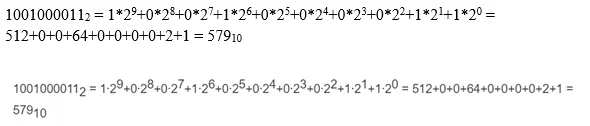
А чтобы было легче, пользуются готовой таблицей степеней 2.

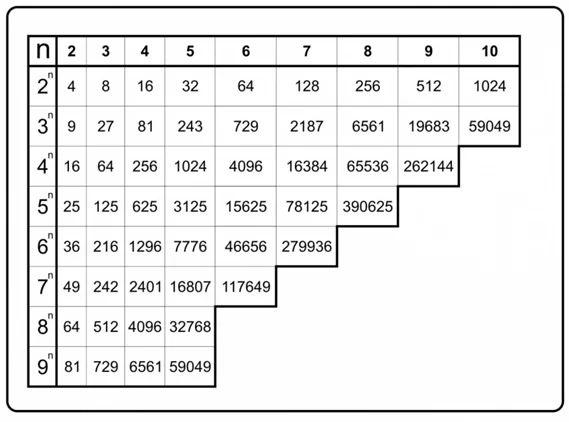
Альтернативный способ преобразования для гуманитариев

Для начала нужно написать степени двойки, начиная с самой большой:

Далее нужно отнимать от числа максимальную степень двойки и напротив нее ставить 1, если есть в исходном варианте или 0, если его нет. Перевод числа 579

Обратно еще проще. Подсчитать количество знаков – это будет степень 2 в степени -1. И так далее. А проще при помощи той же таблицы:

Если же оно на 1 больше, то число будет начинаться и заканчиваться на 1, а внутри – сплошные 0.

Восьмеричная СС

Основой такой системы является 8, а числа восьмеричной системы 0-7. Данная система счисления является позиционной и целочисленной. Применяется в сферах, связанных с цифровыми технологиями, особенно в Linux-программном обеспечении (права доступа, исполнения).

Пример: Перевести 579₈ из десятичной в восьмеричную систему счисления:

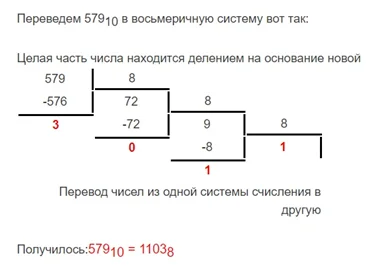
Обратный перевод из восьмеричной СС в десятичную:

1103₈ = 1∙83+1∙82+0∙81+3∙8 = 512+64+0+3 = 579₁₀

Таблица степеней

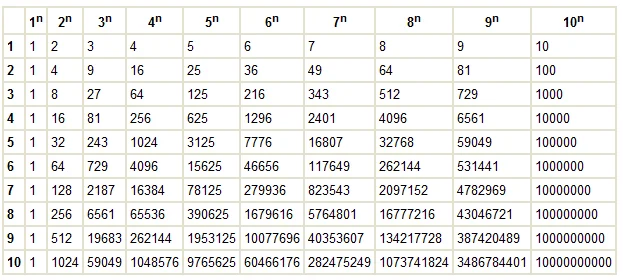
Альтернативный вариант таблицы степеней 

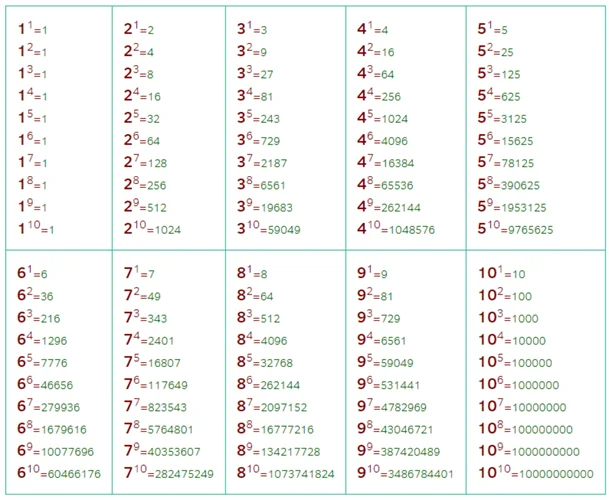
Классификация

Системы исчисления можно разделить на три вида – позиционные, непозиционные и смешанные.

Позиционные

Изобретение данного вида исчисления приписывают древним шумерам. Здесь значение цифры зависит от того, какую позицию она занимает в числе. В качестве примера возьмем число девятнадцать. После перестановки знаков местами получится девяносто один.

Примеры позиционных систем счислений и их использование в математике и информатике:

1. Десятичная – все вы её прекрасно знаете и изучали с первого класса. В качестве алфавита здесь используются цифры от 0 до 9.
2. Двоичная – счисление введенное в семнадцатом веке великим математиком Вильгельмом Лейбницем. В данный момент нашло широкое применение в персональных компьютерах и цифровой технике. Состоит всего из двух знаков 0 и 1.
3. Третичная – состоит из 0, 1 и 2 либо латинских букв A, B, C. На данный момент нигде не применяется. Однако в 1959 году Московским университетом на её основе был выпущен малый компьютер “Сетунь”.
4. Восьмеричная – счисление, широко применяющееся в высокоуровневых языках программирования (например, Java и Python) и разработке цифровой аппаратуры. Свою популярность заслужила из-за легкого перевода в цифровой (двоичный) код. Состоит из цифр от 0 до 7.
5. Двенадцатеричная – распространена на территории Индии и Тибета. Счисление построено на пальце-фаланговом методе счета, при котором большим пальцем считают фаланги той же руки. Попробуйте сами посчитать фаланги, и вы убедитесь, что их действительно 12. Постепенно полностью заменяется десятичной.
6. Шестнадцатеричная – счисление используется в низкоуровневых языках программирования (язык Assembler’а) в информатике. Также в 16-ом виде представляются символы в стандарте Юникода. В её алфавит входят числа от 0 до 9 и латинские буквы A, B, C, D, E и F.

Непозиционные

Здесь позиция цифр значения не имеет, а количественный эквивалент числа определяется начертанием цифры.

Примеры непозиционных нумераций

1. Унарная – состоит из одного символа. В пример можно привезти зарубки на дереве. Также, скорее всего, каждый из вас видел, как в фильмах люди заключенные в тюрьме считают дни своего заключения, рисуя палочки на стене. Всё это примеры унарного исчисления.
2. Римская – состоит из латинских букв I,X,L,D и M. Нумерация построена с помощью сложения и вычитания. Здесь договорились, что для сложения после большей цифры надо ставить меньшую, а для того чтобы отнять, меньшую цифру ставят перед большей. Например, XI – 11, а IX – 9.
3. Египетская – непозиционная нумерация, где цифры представлялись иероглифами.

Смешанные

Этот материал в школьную программу не входит и его достаточно сложно объяснить школьникам, но я все-таки попробую. В смешанной системе исчисления числа с основанием P можно представить числами с основанием Q. Также здесь должно выполняться неравенство Q<P.

0,1,1,2,3,5,8…

Достоинства позиционной системы

Простое выполнение подсчета

У всех позиционных систем одни и те же алгоритмы выполнения арифметических действий. Также в позиционных системах удобно работать с дробями и отрицательными числами, которые зачастую просто невозможно представить в непозиционных системах.

Главные свойства позиционных систем:

• основание всегда записывается внутри системы как 10 (утверждение неприменимо к унарной системе счисления);
• числа можно сравнивать поразрядно, дополнив ведущими нулями до равной длины;
• сложение и вычитание можно выполнять, зная только таблицу сложения однозначных чисел.

Малое количество символов в записи

Позиционные системы используют только десять арабских цифр. Системы с основанием больше десяти добавляют к цифрам 26 латинских букв. В некоторых системах используют круглые и квадратные скобки.

Чем больше основание системы счисления, тем меньшее количество цифр понадобится для записи числа. Числа, состоящие из трех разрядов в десятичной системе, могут иметь всего два разряда в шестнадцатеричной.

Восьмеричная и шестнадцатеричная системы счислений

Компьютерам очень удобно оперировать двоичными числами, но люди не привыкли работать с большим количеством цифр. Например, чтобы представить в двоичном виде число 1234 потребуется больше 10 двоичных цифр (10011010010). Поэтому были придуманы восьмеричная и шестнадцатеричная системы счислений. Они удобны как и десятичные числа тем, что для представления числа требуется меньшее количество разрядов. А по сравнению с десятичными числами, перевод в двоичное представление очень простой. Это как будто мы двоичное число разбили на группы по три или четыре разряда и каждой двоичной комбинации придумали значок. Вот таблица для восьмеричных цифр:

Двоичная комбинация	Значок
000
001	1
010	2
011	3
100	4
101	5
110	6
111	7

А вот таблица для шестнадцатеричных цифр:

Двоичная комбинация	Значок
0000
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

Перевод произвести очень просто, посмотрим на примере числа 010011010010.

Разбиваем его на группы по три цифры: 010 011 010 010. И по таблице переводим: 23228{\displaystyle 2322_{8}}.

Чтобы перевести число в шестнадцатеричное представление разбиваем двоичное число на группы по четыре цифры: 0100 1101 0010. И по таблице переводим: 4D216{\displaystyle 4D2_{16}}. С помощью калькулятора Windows мы можем убедиться, что всё проделано верно.

В программистских кругах шестнадцатеричные числа принято предварять значком 0x (например, 0x4D2), такое написание пошло от языка программирования C, либо значком $ (например, $4D2), такая нотация произошла от языка программирования Pascal. Иногда в литературе используют буквы «h» (от англ. hexadecimal) и «b» (от англ. binary) для обозначения соответственно шестнадцатеричных и двоичных чисел (например, FFh или 1011b).

Двоичная (бинарная) система счисления

Двоичная (или бинарная) система счисления — это позиционная система счисления с основанием 2.

Принцип считать двумя цифрами берёт своё начало ещё в Древнем Китае. Но развитие современной бинарной системы началось в XVII веке, а применение нашлось только в середине XX века.

История двоичной системы счисления

В 1605 году английский астроном и математик Томас Хэрриот описал двоичное представление чисел, а философ Фрэнсис Бэкон создал шифр из двух символов — A и B.

В 1670 году испанский богослужитель Хуан Карамюэль-и-Лобковиц опубликовал представление чисел в разных системах счисления, в том числе и двоичной.

Но самым значительным событием стали работы немецкого математика Готфрида Лейбница, который в 1703 году описал двоичную арифметику — математические операции с двоичными числами.

В 1838 году американский изобретатель Сэмюэл Морзе создал одноимённый шифр, содержащий два символа: «точка» и «тире». Их можно было передавать по телеграфу в виде длинных и коротких сигналов. Азбука Морзе не была бинарной системой в строгом смысле слова, но двоичный принцип впервые показал свою значимость.

В 1847 английский математик Джордж Буль изобрёл «булеву алгебру», в которой было два понятия («ложь» и «истина»), а также ряд логических законов.

В 1937 году американский инженер Клод Шеннон объединил бинарный принцип, булеву логику и электрические схемы и ввёл понятие «бит» — минимальное количество информации:

•  — ложь — нет тока (0 бит);
• 1 — истина — есть ток (1 бит).

С тех пор двоичную (бинарную) систему счисления стали использовать все ЭВМ, в том числе и современные компьютеры.

Числа в двоичной системе счисления

Двоичное число — это число, состоящее из двоичных цифр. А у нас их всего две. Принято обозначать и 1, но, как показала практика, это могут быть и два разных значения: «лампа горит» и «лампа не горит», «ток» и «нет тока» и так далее.

В следующей таблице приведены числа в двоичной системе (зелёный столбец) и соответствующие им числа в других часто используемых системах счисления — восьмеричной, десятичной и шестнадцатеричной.

Изображение: Лев Сергеев для Skillbox Media

Преимущества и недостатки двоичной (бинарной) системы счисления

Явные минусы двоичной системы обусловлены тем, что на интуитивном уровне людям она чужда — в отличие, например, от десятичной. И это — первый недостаток. Пройдёмся по остальным:

Длинная запись, неудобство с большими числами. Возьмём, к примеру, обозначение белого цвета в RGB-палитре: 25510, 25510, 25510 (здесь и далее нижний индекс указывает основание системы — двоичная, десятичная и так далее). Значения цветов принято записывать в шестнадцатеричной системе счисления (FF16, FF16, FF16). Если перевести это в бинарный вид, получится громоздко и непонятно:

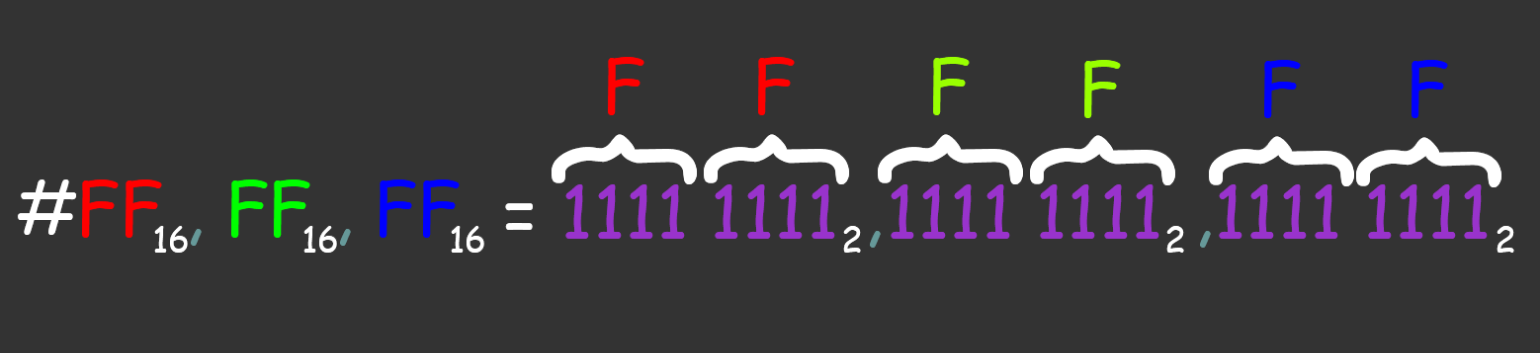
Изображение: Лев Сергеев для Skillbox Media

• Долгое время ручных вычислений.
• Не применяется в повседневной жизни (если, конечно, вы не компьютер).

А вот для ЭВМ бинарочка — как родная. И отсюда следуют её плюсы:

• Позиционная система, имеет разряды.
• Применимы арифметические действия.
• Можно построить логику.
• Подходит для шифровки данных.
• Родной язык компьютерных систем.

Непозиционные системы счисления[]

В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были
расположены в порядке убывания.

Римская система счисления

Каноническим примером фактически непозиционной системы счисления является римская, в которой в качестве цифр используются латинские буквы: I обозначает 1, V — 5, X — 10, L — 50, C — 100, D — 500, M — 1000

Например, II = 1 + 1 = 2
здесь символ I обозначает 1 независимо от места в числе.

На самом деле, римская система не является полностью непозиционной, так как меньшая цифра, идущая перед большей, вычитается из неё, например:

IV = 4, в то время как:
VI = 6

См. римские цифры.

Система остаточных классов (СОК)

Представление числа в системе остаточных классов основано на понятии вычета
и китайской теореме об остатках. СОК определяется набором взаимно-простых модулей (m1,m2,…,mn){\displaystyle (m_{1},m_{2},\dots ,m_{n})} с произведением M=m1⋅m2⋅⋯⋅mn{\displaystyle M=m_{1}\cdot m_{2}\cdot \dots \cdot m_{n}} так, что каждому целому числу x{\displaystyle x} из отрезка ,M−1{\displaystyle } ставится в соответствие набор вычетов (x1,x2,…,xn){\displaystyle (x_{1},x_{2},\dots ,x_{n})}, где

x≡x1(modm1);{\displaystyle x\equiv x_{1}{\pmod {m_{1}}};}

x≡x2(modm2);{\displaystyle x\equiv x_{2}{\pmod {m_{2}}};}

…

x≡xn(modmn).{\displaystyle x\equiv x_{n}{\pmod {m_{n}}}.}

При этом китайская теорема об остатках гарантирует однозначность представления для чисел из отрезка ,M−1{\displaystyle }.

В СОК арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, если про результат известно, что он является целочисленным и также лежит в ,M−1{\displaystyle }.

Недостатками СОК является возможность представления только ограниченного количества чисел, а также отсутствие эффективных алгоритмов для сравнения чисел представленых в СОК. Сравнение обычно осуществляется через перевод аргументов из СОК в смешанную систему счисления по основаниям (m1,m1⋅m2,…,m1⋅m2⋅⋯⋅mn−1){\displaystyle (m_{1},m_{1}\cdot m_{2},\dots ,m_{1}\cdot m_{2}\cdot \dots \cdot m_{n-1})}.

Перевод чисел из СОК в десятичную систему счисления

Формула перевода имеет вид:

A = a₁*B₁+a₂*B₂+…+a_n*B_n-r*P, где a₁, …, a_n — представление числа А в СОК с основаниями p₁, p₂, …, p_n;

P = p₁, p₂, …, p_n;

r = 0,1,2,… (целые числа), причем r выбирают так, чтобы разность между левой и правой частью выражения была меньше P;

B_i = (P/p_i)*k_i, где k_i = 1, 2, …, p_i, причем k_i выбирается таким, чтобы остаток от деления B_i/p_i был равен 1.

Пример.

А = (2,4,6) в системе с основаниями: p₁ = 3, p₂ = 5, p₃ = 7.

P = p₁*p₂*p₃ = 3*5*7 = 105.

B₁ = 105/3*k₁ = 35*2 =70;

B₂ = 105/5*k₁ = 21*1 =21;

B₃ = 105/7*k₁ = 15*1 =15;

A = 2*70+4*21+6*15 — r*105;

A = 314 — r*105 = 104, где r=2.

Системы счисления – виды, особенности

Система счисления (СС) – способ выражения чисел при помощи специальных правил и знаков, которые называются цифрами.

Все существующие системы делят на 2 группы:

1. Позиционные системы счисления – такие, в которых, в зависимости от положения, цифры будет иметь разное значение. К этой группе относится арабская СС, в которой на первом месте справа цифра будет обозначать единицы, на втором – десятки, на третьем – сотни и так далее.

Чтобы выразить число 475, достаточно по порядку написать 3 символа, 475, выражая 5 единиц, 7 десятков и 4 сотни.

К этой группе также относятся СС с различными основаниями (2,8,16).

2. Непозиционные СС – имеет значение именно знак, а не его положение. Единицы, десятки, сотни обозначаются определенными символами. Яркий представитель этой группы – римская СС.

Еще одна особенность – чтобы выразить число и не использовать сотни символов, применяется прибавление и вычитание. Написать 475 римскими знаками можно так CCCCXXXXXXXIIIII, но это нерационально. Если отнимать или прибавлять цифры, получится меньшее количество символов – CDLXXV. Цифра слева означает, что ее нужно отнять от большего числа, а справа – прибавить.

12 – XII

8 – VIII или IIX

Правильным считается тот вариант, при котором получается меньше символов.

Интересно. Первой позиционной СС была вавилонская и была она шестнадцатиричная! А в 19 веке использовали двенадцатеричную СС.

Алфавит СС – знаки, которые используются для обозначения цифр.

Основание – количество знаков, которыми кодируются числа.  Еще оно показывает отличие между цифрами на разных позициях. Основание – целое число, начиная с 2.

Важно. Если в тексте идет речь о различных системах, то чтобы уточнить, какая используется основа, ставится подстрочный знак: 12548, 011001112

Примеры? Если же обозначения нет, по умолчанию это десятичная (12549).

Разряд – положение, позиция обозначения цифры в числе. Пример?

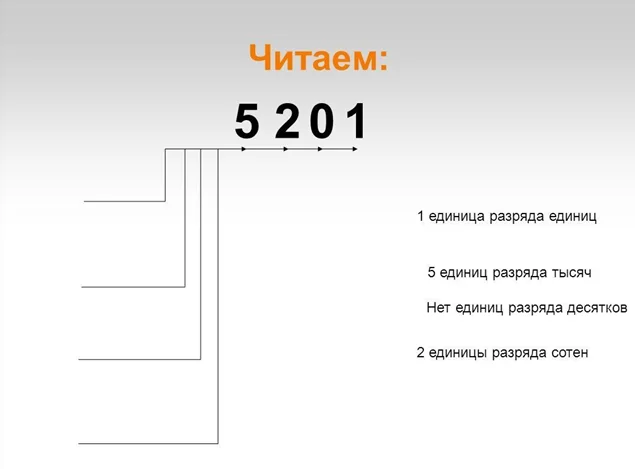
Позиционные системы счисления

Рассмотренные системы счисления относятся к классу позиционных систем. В них числовое значение каждой цифры зависит от положения в числе. Например, в десятичном числе 126 единица означает сотню, а в числе 216 единица уже на другом месте и обозначает десять.

Каждое число позиционной системы счисления можно представить как в свернутом виде, например, 126, так и в развернутом: 1*102 + 2*101 + 6*10 , то есть 100 + 20 +6 =126.

Аналогично, двоичное число 111001 = 1*25 + 1*24 + 1*23 + 0*22 + 0*21 + 1*2

Восьмеричное число: 247 = 2*82 + 4*81 + 7*8

Шестнадцатеричное число: 2A5F = 2*163 + A*162 + 5*161 + F*16

Используя развернутую форму, можно переводить числа из любой системы счисления в десятичную систему.

Классификация позиционных систем

Двоичные

Определение

Двоичная система —  система счисления, в которой в качестве базовых чисел выбираются степени числа два.

Чтобы не путать их с числами, записанными в десятичной системе счисления, справа внизу указывают основание системы счисления. Обычно число при этом заключают в скобки.

Двоичную систему использовали задолго до возникновения информационных технологий. Во втором тысячелетии до нашей эры народы Южной Америки кодировали двоичной системой свои записи, в том числе и не числовые. Узелок и ровный участок нити чередовались друг с другом.

В современной двоичной системе, на основе которой был создан телеграф, а позже — реле и переключатели, единица обозначает наличие сигнала, ноль — его отсутствие. Цифровые электронные схемы работают по тому же принципу. Также на нем основаны сигнальные системы, использующиеся до сих пор, например, азбука Морзе.

Восьмеричные

Когда-то два индейских племени решили, что им удобно при счете смотреть на восемь промежутков между пальцами, а не на сами пальцы. Восьмеричная система счисления отразилась в их языках, в которых только восемь слов, обозначающих цифры.
В двадцатом веке, когда для написания программ требовалось зашифровывать все больше информации в двоичной системе и упростить вычисления для людей, придумали альтернативную систему, которая позволила сократить количество цифр в коде. Число восемь — это два в кубе, поэтому перевести записи из двоичной системы в восьмеричную и обратно проще, чем в десятичную.

Десятичные

Элементы числовой базы, или ключевые числа, в десятичной системе счисления представляют собой степени десяти: 10 = 10^1, 100 = 10^2, 1000 = 10^3.
В системе всего десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Число 10 — основание системы счисления. Цифры от 0 до 9 представляют собой коэффициенты разложения числа по степеням десяти.

Родиной десятичной системы счисления считается Индия, хотя еще в вавилонской цивилизации с ее шестидесятеричной системой использовались закодированные десятичные цифры, а инки в своей узелковой письменности кодировали информацию десятью цветами. Но именно в Индии начали строго соблюдать порядок разрядов числа при записи и ставить ноль, чтобы избежать путаницы. Примерно в середине VIII века эту систему стали использовать другие страны. В Европе она распространилась к XVI веку и была названа «арабской».

Шестнадцатеричные

Шестнадцатеричные системы, как и восьмеричные, появились для упрощения взаимодействия с компьютером. Кроме арабских цифр, в них используются еще и латинские буквы от А до F. В разных языках программирования для записи чисел в шестнадцатеричной системе разные правила, называемые синтаксисом.

Пятеричная

Система, связанная с количеством пальцев на одной руке, использовалась в Китае и у некоторых племен Африки. В китайском языке у иероглифов, обозначающих цифры от шести до девяти, был один и тот же знак в начале — сокращенное обозначение цифры пять. Для записи чисел в этой системе используются цифры 0, 1, 2, 3, 4.

Двенадцатеричная

Если большим пальцем руки сосчитать число фаланг на других пальцах этой руки, получится двенадцать. Группы по двенадцать предметов называли во многих европейских языках словами, схожими с русским словом «дюжина»: duodezim на латыни, douzaine на французском, dozzina на итальянском, dozen на английском. Римляне пользовались двенадцатеричными дробями, \frac1{12} они называли унцией.

В Европе счет дюжинами долгое время, вплоть до XVIII века, сохранялся наравне с десятеричной системой. Дюжина дюжин составляла гросс (от немецкого слова «большой»), дюжина гроссов — массу. Признаки влияния числа 12 заметны в англо-американской системе линейных мер, в которой 1 фут равен 12 дюймам, 1 дюйм — 12 линиям, 1 линия — 6 точкам.

Шестидесятеричная

Первой позиционной системой счисления считается шестидесятеричная система в Древнем Вавилоне. Ее основание до сих пор применяют для измерения времени. Система счисления времени — смешанная, но для перевода минут в секунды или часы потребуется именно шестидесятеричная система.

Для измерения углов и записи координат (широты, долготы) тоже используют эту систему, так как изначально астрономические координаты записывали в шестидесятеричных дробях. По аналогии с часом градус делят на шестьдесят минут, минуту — на шестьдесят секунд.

Двадцатеричная

Двадцатеричную систему называют вигезимальной. Эта система, как и десятеричная, связана с количеством пальцев, поэтому многие народы изобрели ее независимо друг от друга. Основание 20 сохранилось в лингвистической структуре их языков, именно на нем основана система счета в разговорной речи. Например, во французском языке «восемьдесят» состоит из слов «четыре» и «двадцать».

Что такое системы счисления

Системой счисления называется система записи чисел с помощью знаков по определенным правилам.

Символы, с помощью которых записываются числовые значения, обычно называют цифрами, а все вместе знаки системы счисления образуют алфавит. Количество знаков, используемых для обозначения чисел, называется основанием системы счисления.

Приведем примеры чисел систем счисления с различным основанием.

Основная десятичная система, привычная и общеупотребимая, имеет десять символов для обозначения всех чисел, то есть ее основание равно 10. Символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 представляют собой цифры. После цифры 9 в числовом ряду идет двузначное 10. При этом происходит сдвиг разрядной сетки числа влево на один разряд.

Десятичная система использует арабские цифры. Предположительно арабская система записи чисел возникла в Индии. Индийскую систему записи чисел описал Аль Хорезми в своем трактате «Об индийском счете».

Рис. 1. Портрет Аль Хорезми.

Системы счисления в информатике не ограничиваются применением десятичных цифр, самыми распространенными системами являются двоичная, восьмеричная и шестнадцатеричная системы счисления.

В двоичной системе счисления все просто. Основание равно 2. Обозначение чисел выполняется только двумя символами 0 и 1.

Восьмеричная система использует 8 знаков для обозначения чисел: 0, 1, 2, 3, 4, 5, 6, 7

И числовой ряд восьмеричных чисел выглядит так: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12 … Следует обратить внимание, что после 7 идет двузначное число 10, так как знаков всего восемь и происходит сдвиг разрядной сетки

Шестнадцатеричная система имеет основание 16. Она применяет в качестве символов арабские цифры от 0 до 9 и затем буквы латинского алфавита A, B, C, D, E, F. В числовом ряду шестнадцатеричных чисел после 9 идет А, а после F идет 10.

Тогда возникает вопрос, как определить, в какой системе счисления, например число 107. Цифры 0, 1, 7 используются как в восьмеричной, так и в десятичной и шестнадцатеричной системе счисления. Для того чтобы различать системы, существует специальное обозначение систем счисления. Числа помечаются индексом с основанием системы. Так, 107₈ – это восьмеричное число, 107₁₀ – десятичное число, 107₁₆ – шестнадцатеричное число.

в истории существуют примеры использования и других систем счисления. Так, некоторые коренные культуры Африки и Австралии используют двоичные и троичные системы. Индейцы Юки пользуются четверичной системой счисления, пятеричная система счисления распространена больше (по количеству пальцев на руке), ее элементы встречаются у древних персов и ацтеков, у индейцев племени Таманакос. У древних Шумеров использовалась шестидесятеричная система счисления, разбивка часа на 60 минут и минуты на 60 секунд, вероятно, отголоски этой системы.