Ромб — свойства, признаки и формулы нахождения параметров

Основные соотношения

Для решения задач применяются формулы. Ромб не является исключением. Соотношения применяются для определения неизвестных параметров фигуры. Однако бывают случаи, когда недостаточно одной формулы, поскольку нужно связать несколько компонентов в единый процесс вычислений. Для корректного использования формул следует ввести класс некоторых обозначений:

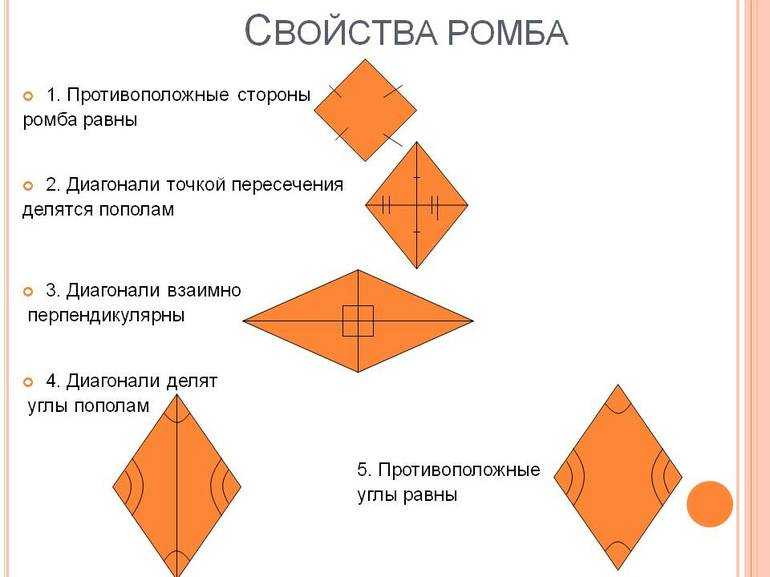
1. Ромб обозначить набором латинских букв ABCD.
2. Стороны приравнять к некоторому числу, заданному в общей форме: AB = BC = CD = DA = a.
3. Диагонали: меньшая — m2 и большая = m1. Их точку пересечения следует обозначить литерой P.
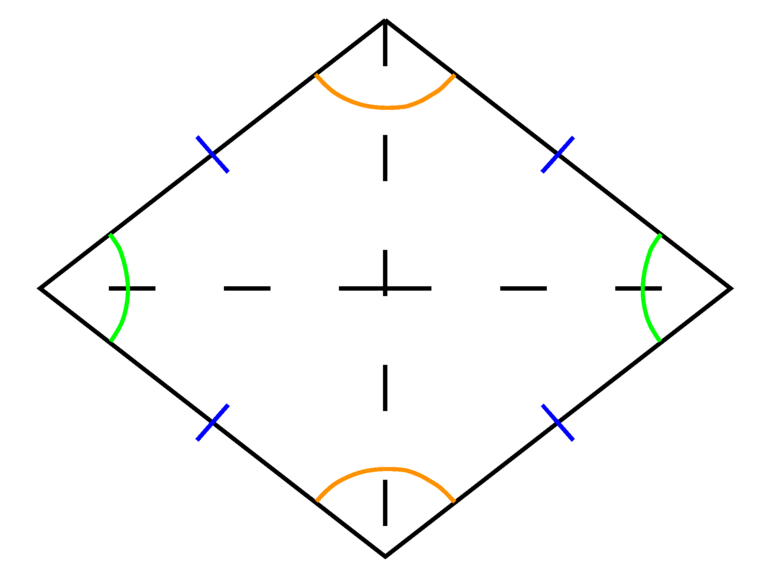
4. Углы: ∠ABC = ∠ADC и ∠BAD = ∠BCD.
5. Характеристики вписанной окружности: диаметр D и радиус R.
6. Периметр и площадь (размерность): P и S соответственно.

Периметр и площадь

Периметр ромба — характеристика, которая эквивалентна значению алгебраической суммы всех ее сторон. Площадью называется параметр геометрической фигуры, показывающий ее размерность в определенном геометрическом пространстве. Следует отметить, что величина S существует только у фигуры в двумерном пространстве. В трехмерном нужно рассматривать объем геометрического тела. Кроме того, у объемного тела есть параметр площади поперечного сечения. Эта величина является двумерной.

Периметр вычисляется по следующей формуле: P = 4 * a. Следует отметить, что величину a можно выражать через диагонали, площадь и другие характеристики. Базовая формула площади ромба имеет такой вид: S = a * BP = a * DP = a * AP = a * CP. Кроме того, размерность можно найти по следующим соотношениям:

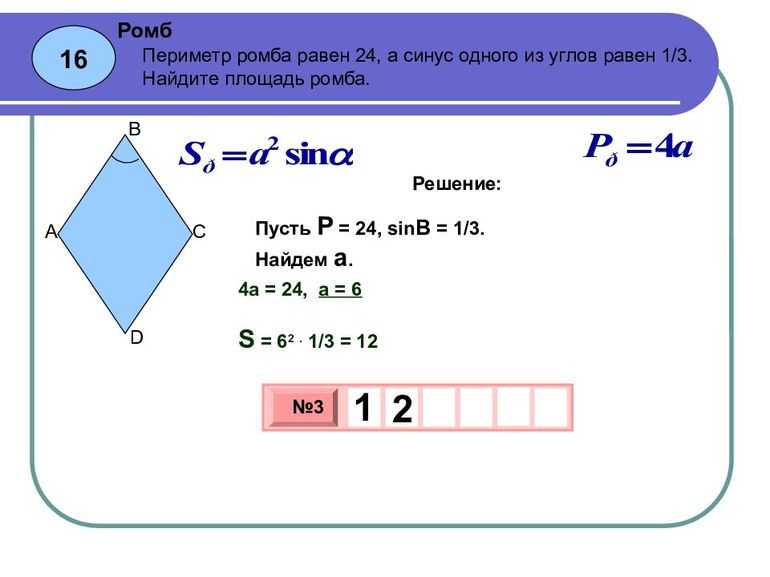
1. S = a 2 * sin (∠ABC) = a 2 * sin (∠BCD) (через синус острого угла).
2. S = 2 * a * R.
3. S = (m1 * m2) / 2.
4. S = (4 * R 2) / sin (∠BAD).
5. S = [(m1)^2 * tg (∠BAD / 2)] / 2 = [(m2)^2 * tg (∠ABC / 2)] / 2.

Нахождение стороны

Длина стороны находится очень просто, поскольку математики выполнили доказательства некоторых тождеств. Они предлагают готовые решения в виде формул, позволяющих правильно выразить одну величину через другую, и подставить необходимые числовые значения:

1. a = S / BP = S / DP = S / AP = S / CP.
2. a = S^(½) / (sin (∠BAD))^(½).
3. a = S / 2 * R.
4. a = ^(½) / 2.
5. a = P / 4.

Необходимо обратить внимание, что используются в некоторых соотношения тригонометрические функции. Последнее соотношение является формулой определения периметра

Если он известен, то легко вычислить значение стороны, используя обратную формулу P.

Другие соотношения

Осталось еще два параметра ромба — диагонали. Специалисты рекомендуют воспользоваться готовыми соотношениями для нахождения ее длины:

1. m1 = 2 * a * cos (∠BAD/2).
2. m2 = 2 * a * sin (∠BAD/2).

3. m1 = ^(½) = ^(½).

4. m2 = ^(½) = ^(½).

5. m1 = 2 * S / m2.
6. m2 = 2 * S / m1.

Следует также рассмотреть случай, когда окружность вписана в ромб. Такой прием применяется для расширения возможностей поиска неизвестной, что существенно позволит сэкономить время на расчетах. К формулам относятся следующие тождества:

1. R = S / 2 * a.
2. R = m1 * m2 / (2 * ((m1)^2 + (m2)^2)^(½)).
3. R = m1 * m2 / P = m1 * m2 / 4 * a.

Свойства и признаки прямоугольника

Тип утверждения	Фигура	Рисунок	Формулировка
Определение	Прямоугольник		Прямоугольником называют , у которого все углы прямые
Свойство	Равенство		Если является , то его диагонали равны
Признак	Если у диагонали равны, то он является

Определение: прямоугольник
	Прямоугольником называют , у которого все углы прямые
Свойство: равенство
	Если является , то его диагонали равны
Признак: равенство
	Если у диагонали равны, то он является

Прямоугольник

Определение: Прямоугольником называют , у которого все углы прямые.

Равенство

Свойство: Если является , то его диагонали равны. Признак: Если у диагонали равны, то он является .

Общие сведения

Ромб является четырехугольником. В геометрии существует несколько видов последних. Для каждой фигуры предусмотрены свои соотношения, теоремы и формулы. Кроме того, математики выделяют специализированные алгоритмы, позволяющие точно и без ошибок определить тип фигуры.

Ученые разработали алгоритм для обучения, позволяющий за короткий промежуток времени перейти к решению сложных математических упражнений без каких-либо финансовых вложений. Он состоит из следующих элементов:

1. Сведения о ромбе: признаки, свойства и теоремы.
2. Формулы для нахождения некоторых параметров.

Как нарисовать ромб

Нарисовать такую фигуру как ромб можно несколькими способами. В этой статье мы рассмотрим два простых способа.

Для первого способа нам понадобятся: ручка или карандаш, ластик, лист в клетку из школьной тетради, линейка или любой похожий на него прямой предмет, если размеры точные размеры ромба не важны.

• Итак, для начала нарисуем точку на одном из пересечений линий клеток. Лучше, конечно, разместить точку не слишком близко к краям. Определяемся с размерами фигуры.
• Далее от средней точки отсчитываем необходимое количество клеток влево (или вправо) и ставим еще одну точку. В противоположной стороне через такое же количество клеток рисуем третью точку. Теперь то же самое проделываем по направлению вверх и вниз. Последовательность не имеет значения, главное здесь – отсчитать одинаковое расстояние от средней точки влево и вправо и отдельно вверх и вниз. То есть, если направо отсчитали четыре клетки, а вверх шесть клеток, соответственно, влево четыре клетки, вниз шесть клеток.

Соединяем линейкой или любым другим подходящим предметом все точки между собой, кроме среднего. Среднюю точку можно стереть ластиком, если вы использовали карандаш. Ромб готов.

Второй способ аналогичен первому, но рисовать мы будем на чистой бумаге без клеток. Нам нужно для этого: карандаш и/или ручка, ластик, чистый лист, линейка и угольник (или любой предмет с прямым углом).

1. Определяемся с размерами. Рисуем точку.
2. Берем линейку, ставим точку на необходимом расстоянии от средней точки на левой стороне. Соединяем их карандашом, чтобы линия проходила через среднюю точку. Аналогичные действия производим и в противоположную сторону.
3. Также рисуем точку сверху и снизу, но уже пользуемся угольником, чтобы линия между верхней и нижней точкой была перпендикулярна линии между левой и правой.
4. Соединяем все точки между собой. Стираем ластиком линии посередине фигуры.

Признаки ромба

Признак 1. Если смежные стороны параллелограмма равны, то этот параллелограмм − ромб.

Доказательство. Пусть смежные стороны параллелограмма ABCD равны. То есть имеем: AB=BC (Рис.3). У параллелограмма противоположные стороны равны (Свойство 1 статьи Параллелограмм). Тогда DC=AB=BC=AD. То есть все стороны параллелограмма равны и по определению 1, этот параллелограмм является ромбом.

Признак 2. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм − ромб.

Доказательство. Пусть диагонали параллелограмма ABCD перпендикулярны (Рис.3). Рассмотрим прямоугольные треугольники AOB и COB. Так как у параллелограмма диагонали точкой пересечения разделяются пополам (Свойство 2 статьи Параллелограмм), то AO=OC. Тогда прямоугольные треугольники AOB и COB равны по двум катетам (AO=OC, BO общий катет (см. статью Прямоугольный треугольник. Свойства, признаки равенства)). Следовательно AB=BC. Тогда по признаку 1 этот параллелограмм является ромбом.

Признак 3. Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм − ромб.

Доказательство. Пусть диагональ AC параллелограмма ABCD является биссектрисой угла BAD (Рис.4). Тогда \( \small \angle 1= \angle 2 .\) У параллелограмма ABCD \( \small AB \ || \ DC .\) Тогда для параллельных прямых AB и DC и секущей AC справедливо равенство \( \small \angle 1= \angle 4 .\) (см теорему 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично, для параллельных прямых BC и AD и секущей AC справедливо равенство \( \small \angle 2= \angle 3 .\) Так как \( \small \angle 1= \angle 2 ,\) то \( \small \angle 1= \angle 2=\angle 3= \angle 4 .\) Из \( \small \angle 1= \angle 3\) следует, что треугольник ABC равнобедренный (Признак 2 статьи Равнобедренный треугольник). Тогда AB=BC. У параллелограмма противоположные стороны равны (Свойство 1 статьи Параллелограмм). Тогда AB=BC=CD=DA. То есть все стороны параллелограмма равны и по определению 1, этот параллелограмм является ромбом.

Признак 4. Если стороны четырехугольника равны, то этот четырехугольник − ромб.

Доказательство. Пусть у четырехугольника все стороны равны. Тогда этот четырехугольник является параллелограммом (признак 2 статьи Параллелограмм). А по определению 1, этот параллелограмм является ромбом.

Определение ромба, как геометрической фигуры

Ромб — это такой параллелограмм, у которого все стороны равны. Если же ромб имеет прямые углы, то он называется квадратом.

Сам термин «Ромб» в переводе с греческого языка, обозначает «бубен». Конечно же в нашем понимании бубен, как музыкальный инструмент, имеет круглую форму. Но это сейчас бубны делают круглыми, а в древние времена он как раз и имел квадратную форму или форму ромба.

Давайте остановимся на основных определениях ромба и попробуем понять, что же являет собой эта геометрическая фигура.

Ромб – это такой равносторонний параллелограмм, у которого равные стороны, но неравные углы.

Ромбом можно считать и равносторонний четырехугольник, который имеет два противоположных угла острых и два тупых.

В отличие от квадрата, ромб – это равносторонний косоугольник.

Как всегда мы получаем множество определений той или иной геометрической фигуры, но это не означает, что каждый ученик должен сесть и «зазубрить» именно эти определения. Отличие в определениях – это насколько широко они описывают нашу геометрическую фигуру. Самое главное, это понимание о чем говориться в определении и возможность представить фигуру. Если вы будете придерживаться этих двух правил, то и сами сможете написать или дополнить парочку определений.

Окружность вписанная в ромб

Формулы определения радиуса круга вписанного в ромб:

1. Формула радиуса круга вписанного в ромб через высоту ромба:

r =	h
2

2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:

r =	S
2 a

3. Формула радиуса круга вписанного в ромб через площадь и синус угла:

r =	√ S · sinα
2

4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:

r =	a · sinα
2

r =	a · sinβ
2

5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:

r =	d 1 · sin ( α /2)
2

r =	d 2 · sin ( β /2)
2

6. Формула радиуса круга вписанного в ромб через две диагонали:

r =	d 1 · d 2
2√ d 1 2 + d 2 2

7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:

r =	d 1 · d 2
4 a

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool. Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Как нарисовать ромб

Чтобы нарисовать ромб воспользуемся свойствами диагоналей ромба. Нам уже известно, что диагонали нашей геометрической фигуры взаимно перпендикулярны и делятся пополам в точке пересечения. Поэтому построение ромба проще всего начать с построения его диагоналей.

Первый способ

И так, в первую очередь выбираем точку, от которой откладываем влево и право отрезки одной длины, в вверх и вниз одинаковые отрезки другой длины.

Теперь нам остается только соединить концы этих отрезков, и в результате мы получим ромб.

Второй способ

Ромб можно еще начертить без использования диагоналей. В этом случае нужно определить лишь концы диагоналей и потом соединить точки отрезками.

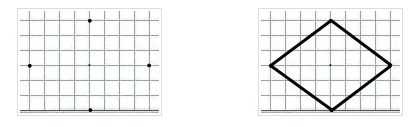
Третий способ

И наконец, третий способ, черчения ромба можно выполнить при помощи линейки. Так как мы с вами знаем, что ромб имеет равные стороны, то вначале нужно нарисовать его нижнюю часть. Затем необходимо отложить от нее равный отрезок. А так как третья сторона параллельна первой, то соединив концы первого и третьего отрезков, мы получим ромб.