Сформулируйте и докажите утверждение о пропорциональных отрезках в прямоугольном треугольнике кратко

Задачи на построение

Подобие помогает решать некоторые задачи, связанные с построением фигур. Пусть требуется построить треуг-к, если известны только два его угла, а также длина биссектрисы, выходящей из третьего угла. Решение состоит из 5 шагов:

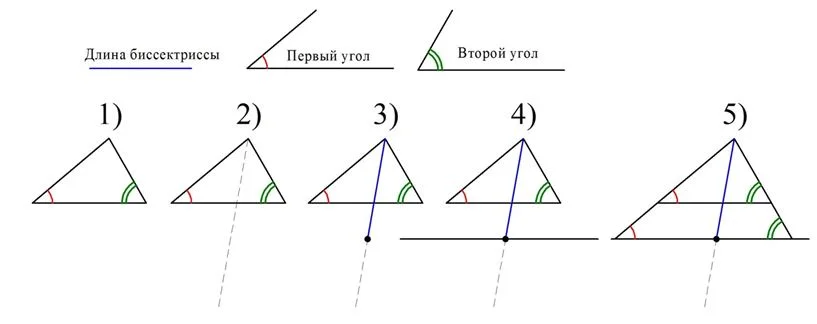
На первом шаге строится произвольный треуг-к, в котором два угла равны заданным в условии. На втором шаге третий угол получившегося треуг-ка разбивается пополам, то есть строится его биссектриса, причем она строится в виде луча, а не конечного отрезка. На третьем шаге на этом луче откладывается отрезок, длина которого совпадает с заданной длиной биссектрисы. В результате на луче можно отметить точку, которая соответствует концу этого отрезка. На шаге 4 через эту точку проводится прямая, параллельная основанию уже построенного треуг-ка. Наконец, на последнем шаге стороны треуг-ка продлеваются до пересечения с новой прямой. В итоге получается новый треуг-к, который будет соответствовать условиям задачи.

2. Углы в прямоугольном треугольнике

Те­перь рас­смот­рим пря­мо­уголь­ные тре­уголь­ни­ки.

По­сколь­ку в пря­мо­уголь­ных тре­уголь­ни­ках все­гда есть пара рав­ных углов (это пря­мые углы), то для них можно сфор­му­ли­ро­вать сле­ду­ю­щий при­знак по­до­бия: пря­мо­уголь­ные тре­уголь­ни­ки по­доб­ны, если имеют рав­ные ост­рые углы (см. Рис. 2).

Рис. 2

.

При этом от­ме­тим важ­ный факт: в пря­мо­уголь­ных тре­уголь­ни­ках сумма ост­рых углов равна : 

Рас­смот­рим про­стую за­да­чу для пря­мо­уголь­но­го тре­уголь­ни­ка.

Дано:  – пря­мо­уголь­ный (), ,  – вы­со­та.

Найти: осталь­ные углы тре­уголь­ни­ка (см. Рис. 3).

Ре­ше­ние:   

Для ре­ше­ния за­да­чи будем ис­поль­зо­вать сфор­му­ли­ро­ван­ный выше факт: сумма ост­рых углов пря­мо­уголь­но­го тре­уголь­ни­ка равна 

Рис. 3

 . Зна­чит, .

Кроме того, тре­уголь­ник  – также пря­мо­уголь­ный, по­это­му сумма его ост­рых углов также равна   (см. Рис. 4).

Ана­ло­гич­но с тре­уголь­ни­ком : .

Рис. 4

Из этого свой­ства пря­мо­уголь­но­го тре­уголь­ни­ка и его вы­со­ты, про­ве­дён­ной к ги­по­те­ну­зе, сле­ду­ет несколь­ко важ­ных фак­тов.

Рас­смот­рим пря­мо­уголь­ный тре­уголь­ник с вы­со­той, ко­то­рая про­ве­де­на к ги­по­те­ну­зе (см. Рис. 5).

Рис. 5

 – про­ек­ция ка­те­та  на ги­по­те­ну­зу ,  – про­ек­ция ка­те­та  на ги­по­те­ну­зу  – это стан­дарт­ные обо­зна­че­ния.

На Рис. 5 изоб­ра­же­но три пря­мо­уголь­ных тре­уголь­ни­ка , при­чём в каж­дом из них есть ост­рый угол . Зна­чит, эти тре­уголь­ни­ки по­доб­ны по пер­во­му при­зна­ку по­до­бия для пря­мо­уголь­ных тре­уголь­ни­ков: .

Средняя линия треугольника

Отметим в треугольнике середины двух сторон и соединим их. В итоге получится отрезок, который именуют средней линией треугольника.

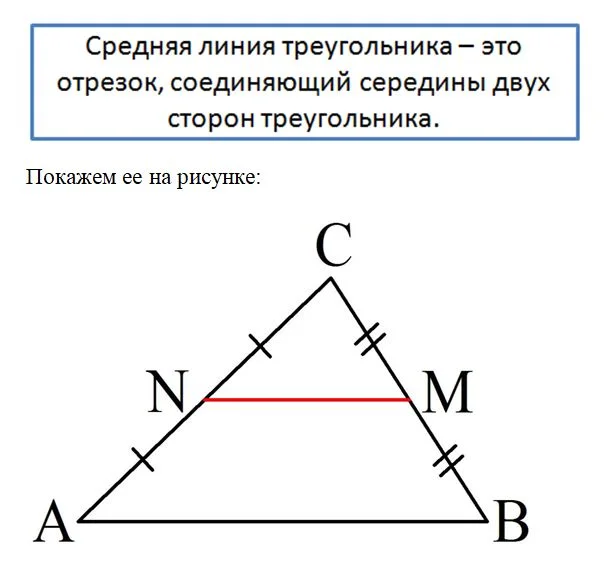
Здесь точки N и M– это середины АС и ВС соответственно, поэтому NM – это средняя линия

Обратим внимание на ∆АBС и ∆СNM. По рисунку видно, что они подобны, и это действительно так

Ясно, что отношение отрезков АС и СN равно 2, ведь середина N разбивает АС на отрезки, которые вдвое меньше АС:

При этом ∠С является общим для обоих треуг-ков. Это значит, что ∆АBС и ∆NMC подобны (по второму признаку подобия треугольников), причем коэффициент их подобия равен 2. Отсюда сразу следует, что и NM вдвое короче, чем АB.

Из подобия треугольников также следует, что

Но эти два угла являются соответственными для отрезков АB и NM и их секущей AN. Из равенства соответственных углов вытекает, что отрезки АB и NM параллельны. В итоге можно сформулировать два основных свойства средней линии:

Задание. Найдите длину средней линии треугольника FDE, параллельной стороне DE:

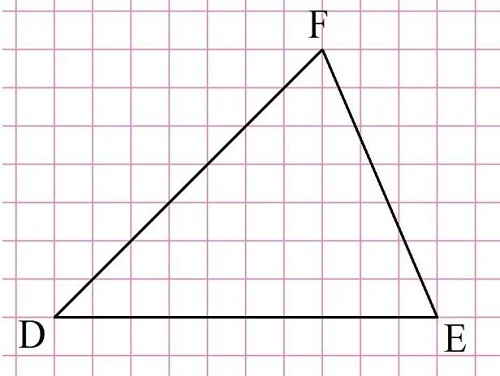
Решение. Средняя линия будет вдвое короче DE. Видно, что DE имеет длину 10 клеточек, значит, средняя линия равна 10:2 = 5.

Ответ: 5.

Задание. Стороны треуг-ка имеют длину 8, 5 и 7 см. Середины всех сторон соединили отрезками и получили новый треуг-к. Каков его периметр?

Решение. В данном задаче в треуг-ке построили не одну, а сразу 3 средние линии:

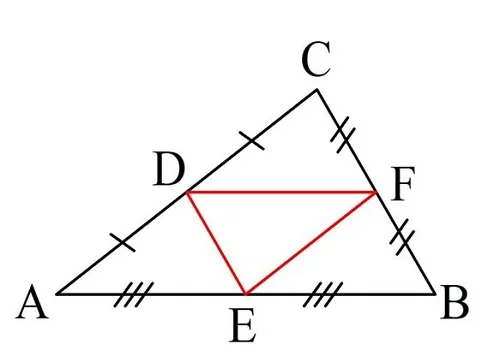
Пусть стороны АB, АС и ВС соответственно составляют 8, 7 и 5 см. Тогда средние линии, параллельные им, будут вдвое меньше:

Задание. Докажите, что три средние линии треуг-ка разбивают его на 4 равные части.

Решение. Пусть стороны треуг-ка равны а, b и с.Отметим середины каждой стороны. Эти середины разобьют стороны на отрезки длиной а/2, b/2 и с/2. Средние же линии, построенные в треуг-ке, будут вдвое меньше сторон значит, их длина также будет составлять а/2, b/2 и c/2:

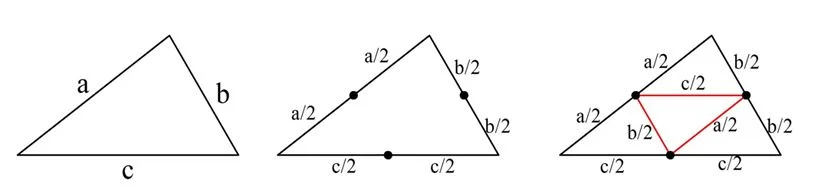
В итоге у каждого из получившегося треуг-ка стороны равны величинам а/2, b/2 и c/2. Значит, по 3-ему признаку равенства треуг-ков, они все равны друг другу, ч. т. д. 

Задание. В произвольном четырехугольнике отрезками соединили середины смежных сторон. Докажите, что эти отрезки образуют параллелограмм.

Решение. Отметим буквами M, E, Fи H середины сторон четырехуг-ка АBСD. Также построим диагонали АС и BD:

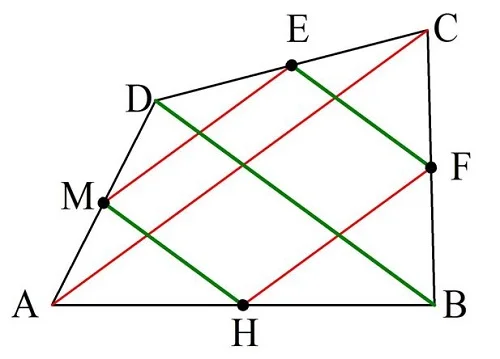
Легко заметить, что МН оказывается средней линией в ∆АBD, ведь она соединяет середины AD и AB. Значит, МН параллельна BD. Но и EF в свою очередь – это средняя линия в ∆BDC, и поэтому она также параллельна BD. Но два отрезка, параллельные третьему, должны быть параллельны и друг другу, то есть МН||EF.

Аналогично и отрезки МЕ и HF – это средние линии в ∆АСD и ∆АBС, поэтому они оба параллельны АС, а значит, и друг другу. В итоге в четырехуг-ке МНFE противоположные стороны оказываются параллельными. Это значит, что он по определению является параллелограммом.

Примечание. Геометрия – наука, развивавшаяся ещё во времена Античности, и большинство теорем и фактов из школьного курса было известно ещё древним грекам. Однако тот приведенный выше факт, что середины любого четырехуг-ка образуют параллелограмм, был доказан только в XVII в. французом Пьером Вариньоном. Соответственно, такой параллелограмм называют вариньоновским.

Вариньоновский параллелограмм обладает множеством свойств. В частности, его площадь вдвое меньше площади исходного четырехуг-ка, а периметр – это сумма длин его диагоналей. Попробуйте самостоятельно доказать это.

Практические задачи

Подобие треуг-ков может быть использовано и на практике, для измерения некоторых размеров. Например, пусть надо измерить высоту одиноко стоящего дерева. Для этого можно просто поставить рядом, например, человека, чей рост известен. Далее надо измерить длину тени этого человека и самого дерева:

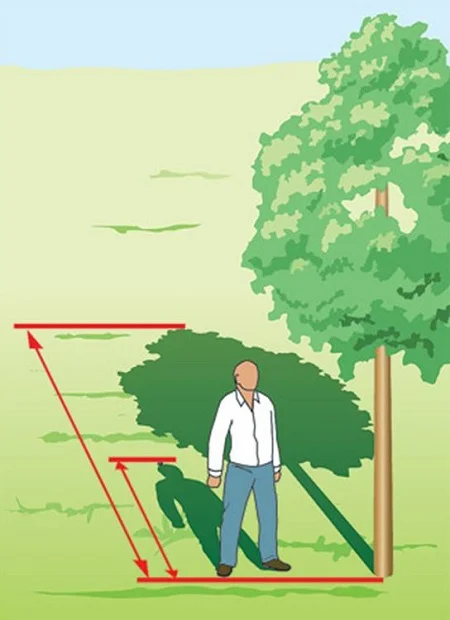
Так как тень должна падать под одним и тем же углом, то в итоге можно получить два подобных треугольника:

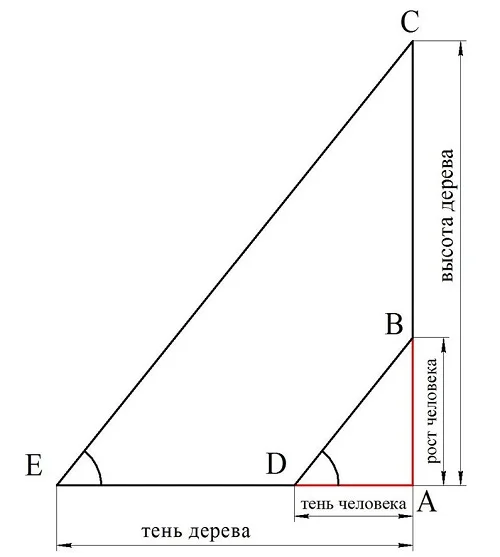
Например, пусть высота человека составляет 1,8 м, а тени человека и дерева имеют протяженность 1,2 и 4,8 м. На рисунке ∆АBD и ∆АСЕ подобны, причем стороны AD и АЕ – сходственные. Поделим их чтобы найти коэффициент подобия треугольников:

Также подобие помогает находить расстояние до недоступных точек, например, до горных вершин. Пусть точка В недоступна нам. Выберем две доступные нам точки А и С и измерим расстояние между ними. Также измерим∠А и ∠С в ∆АBС (для этого используется какой-нибудь прибор, например, астролябия). Далее построим на бумаге треуг-к А₁В₁С₁ с такими же углами, но меньшей длиной А₁С₁:

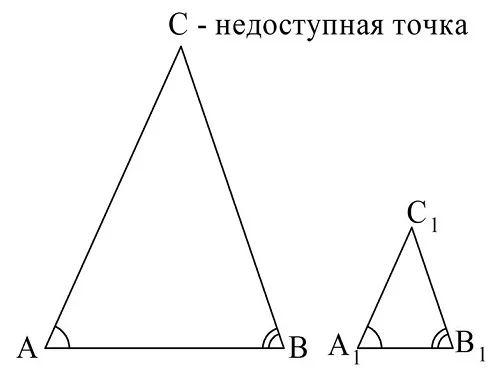
При построении можно выбрать определенный масштаб, например, 1:1000. Так, если реальная длина АB оказалась равной 57 метрам, то на чертеже отрезок А₁В₁ должен быть в тысячу раз короче, то есть равен 57 мм (в 1 метр как раз составляет 1000 мм). Далее на чертеже измеряют длину А₁С₁. Пусть она оказалась равной 519 мм. Тогда длина реального размера АС будет составлять уже 519 метров.

Средняя линия трапеции

Напомним, что ранее мы уже изучили другую среднюю линию, которую можно провести в трапеции. Мы доказали, что она параллельна основаниям трапеции. Попробуем найти способ для нахождения ее длины.

Пусть точки M и N – середины боковых сторон АB и CD трапеции АBСD. Построим отрезок BN, а далее продлим прямые BN и AD до их пересечения в некоторой точке K:

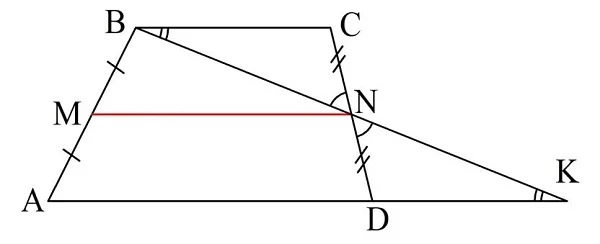
Посмотрим на ∆ВNC и ∆KND. У них есть два одинаковых угла:

Отсюда вытекает, что эти треуг-ки подобны (по первому признаку подобия), причем стороны ND и CN – сходственные. Однако эти же отрезки одинаковы, ведь N – середина СD. То есть коэффициент подобия треуг-ков – единица. Это означает, что ∆ВСN и ∆KND равны, и тогда ВС = DK, а. Следовательно, длина АК равна сумме длин оснований трапеции:

Из равенства треуг-ков также вытекает, что BN = NK, то есть N– это середина BK. Но тогда MN по определению – это средняя линия для ∆АBK. Значит, она составляет половину AK, которая в свою очередь является суммой оснований трапеции:

Задание. Найдите длину средней линии трапеции, показанной на рисунке:

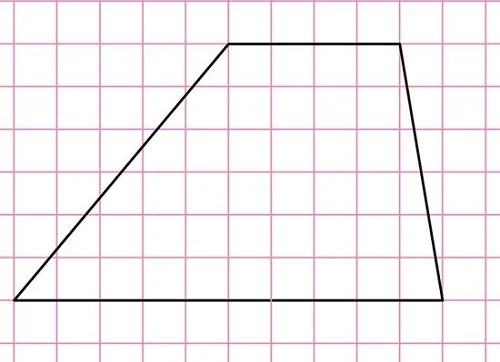
Решение. По рисунку видно, что основания имеют длины 10 и 4. Надо лишь сложить эти числа и поделить их надвое:

(10 + a):2 = 14:2 = 7

Ответ: 7.

Задание. Длины боковых сторон трапеции имеют длину 13 и 15 см, ее периметр составляет 48 см. Вычислите длину ее средней линии.

Решение. Задачу можно решить и без рисунка. Обозначим основания трапеции буквами a и b. Периметр – это сумма всех сторон фигуры, поэтому, зная его и длины боковых сторон, можем составить уравнение, из которого найдем величину a + b:

Задание. Докажите, что средняя линия трапеции делит ее диагонали пополам.

Решение. Обозначим середину диагонали BD трапеции АBСD как точку К. Нам надо доказать, эта точка лежит на средней линии MN. Будем доказывать способом «от противного». Пусть точка K не лежит на MN:

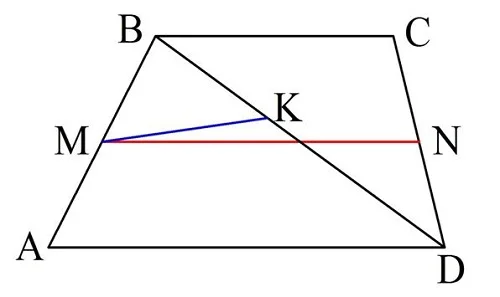
Тогда МК будет средней линией в ∆АBD, ведь она соединяет середины АB и BD. Значит, отрезок МК параллелен AD. Аналогично и МN как средняя линия в АBСD также параллельна AD. Однако тогда получается, что через точку М проходят сразу две прямые, параллельные AD, что противоречит аксиоме параллельности. Значит, K не может НЕ лежать на MN, то есть эта точка лежит на средней линии.

Очевидна схожесть формул для вычисления средней линии как в трапеции, так и в треуг-ке. Эта схожесть подсказывает нам, что треуг-к можно рассматривать как особый частный случай трапеции, у которой одно из оснований как бы «стянулось» в точку и стало иметь нулевую длину. Такие частные случаи в математике называются вырожденными.

4. Доказательство теорем

Тео­ре­ма 1. .

До­ка­за­тель­ство:

Вос­поль­зу­ем­ся по­до­би­ем тре­уголь­ни­ков . За­пи­шем от­но­ше­ние со­от­вет­ству­ю­щих сто­рон:  (от­но­ше­ние сто­рон, ле­жа­щих про­тив угла , равно от­но­ше­нию сто­рон, ле­жа­щих про­тив угла ). Из этой про­пор­ции по­лу­ча­ем: . Или: .

До­ка­за­но

Тео­ре­ма 2. .

До­ка­за­тель­ство:

Вос­поль­зу­ем­ся по­до­би­ем тре­уголь­ни­ков . За­пи­шем от­но­ше­ние со­от­вет­ству­ю­щих сто­рон: . (от­но­ше­ние сто­рон, ле­жа­щих про­тив угла , равно от­но­ше­нию сто­рон, ле­жа­щих про­тив угла ). Из этой про­пор­ции по­лу­ча­ем: . Или: .

До­ка­за­но.

Тео­ре­ма 3. .

До­ка­за­тель­ство

Вос­поль­зу­ем­ся по­до­би­ем тре­уголь­ни­ков . За­пи­шем от­но­ше­ние со­от­вет­ству­ю­щих сто­рон:  (от­но­ше­ние сто­рон, ле­жа­щих про­тив угла , равно от­но­ше­нию сто­рон, ле­жа­щих про­тив угла ). Из этой про­пор­ции по­лу­ча­ем: . Или: .

До­ка­за­но.

Прямоугольные треугольники

Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).

Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.

2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.

3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)

4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.

5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$

6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$

7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

В прямоугольном треугольнике $АВС$ для острого угла $В$:

5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.

6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.

7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	$/$	$/$	$/$
$cosα$	$/$	$/$	$/$
$tgα$	$/$	$1$	$√3$
$ctgα$	$√3$	$1$	$/$

Площадь прямоугольного треугольника равна половине произведения его катетов

В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√$. Найдите косинус внешнего угла при вершине $В$.

Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то

Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:

Катет $ВС$ мы можем найти по теореме Пифагора:

Подставим найденное значение в формулу косинуса

В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sin⁡A=/, AC=9$. Найдите $АВ$.

Распишем синус угла $А$ по определению:

Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.

Применим теорему Пифагора, чтобы отыскать $«х»$

Так как длина $АВ$ составляет пять частей, то $3∙5=15$

В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:

Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.

В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.

Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.

Свойство биссектрисы

В заключение рассмотрим одно важное свойство биссектрисы, которое напрямую не связано с подобием, однако использует понятие пропорциональных отрезков. Пусть в ∆АBС, в котором известны стороны АС и ВС, проведена биссектриса СМ

Она разбивает АB на два отрезка, АМ и МВ. Можно ли что-то сказать о длине АМ и МВ?

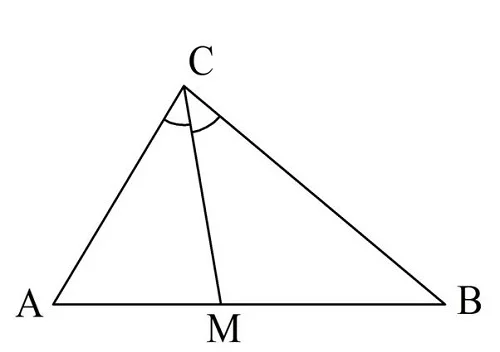
Оказывается, биссектриса будет делить АB на отрезки, которые окажутся пропорциональными сторонам АС и ВС. Докажем это.

Опустим из точки М высоты на МD и MF на стороны АС и ВС:

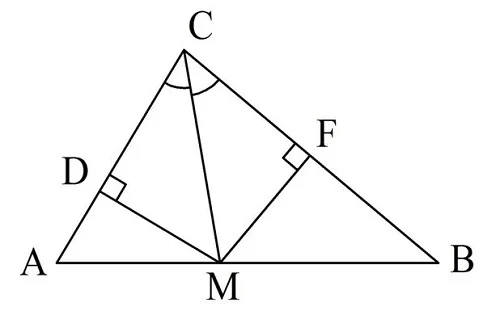
Исследуем ∆СМD и ∆СМF. Они прямоугольные, причем у них общая гипотенуза СМ и одинаковые острые углы (∠МСD = ∠МСF, ведь МС – биссектриса). Следовательно, они равны, и тогда высоты МD и МF оказываются одинаковыми:

Теперь запишем эти же площади, проведя другую высоту, СН, которая будет общей для ∆АСМ и ∆СМВ:

В итоге получили вывод:

Задание. AD – биссектриса в ∆АBС. Известно, что

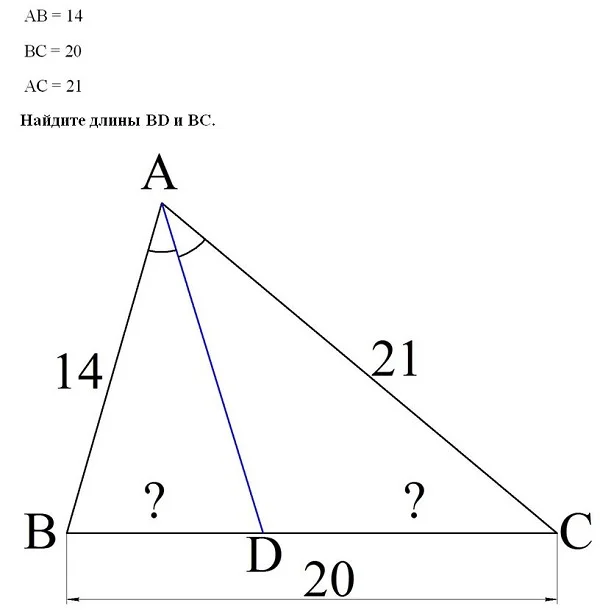
Решение.Отношение отрезка BD к DC равно отношению АB к АС:

Сегодня мы увидели, что пропорциональные отрезки в треугольнике возникают и при выполнении множества построений, а подобие фигур позволяет на практике находить размеры, которые сложно измерить непосредственно. Это подчеркивает практическую значимость изучения геометрии.

Пропорциональные отрезки в прямоугольном треугольнике — отношение

Определение

Средним пропорциональным двух величин a и b называется число c при условии, что квадрат c равен произведению a и b, то есть c2=ab.

На рисунке изображен прямоугольный треугольник с катетами a и b, гипотенузой c и проведенной к ней высоте h. Высота делит гипотенузу на два отрезка: a_c и b_c, именуемые проекциями катетов на гипотенузу.

Теорема 1

Среднее пропорциональное между гипотенузой и проекцией на нее – это каждый катет прямоугольного треугольника, то есть:

\(a^2=a_c\times c \)

\(b^2=b_c\times c\)

Доказательство

Пусть в ΔABC ∠C=90°, ∠A=α, CH – высота.

1. Сначала докажем, подобие ΔABC и ΔCBH.  

Поскольку CH – высота, то ∠CHB равен 90°.

∠B=90°−α – это общий угол рассматриваемых треугольников ABC и CBH.

∠HCB=90°−∠B=90°−(90°−α)=α.

Следовательно, в ΔABC и ΔCBH: 

∠ACB=∠HCB=90°

∠B – общий и равен 90°−α

∠CAB=∠HCB=α

Отсюда следует, что ΔABC∼ΔCBH.

2. Теперь докажем, что ΔABC∼ΔACH. 

∠ACB=∠AHC=90°, т.к. СН – высота ΔABC.

∠A – общий и равен α.

∠ACH=90−α, а значит, равен ∠AВC.

Следовательно, ΔABC∼ΔACH.

3. Сделаем на схеме дополнительные обозначения проекций катетов:

4. Применим доказанное подобие ΔABC и ΔCBH и запишем пропорции сторон: 

\(\frac ac=\frac{a_c}a\)

В переводе с математического языка это означает следующее: отношение противолежащих прямому углу сторон, ровняется отношению сторон, расположенных напротив угла α. Из данного соотношения получается:

\((1)a^2=a_c\times c\)

5. Воспользуемся тем, что ΔABC∼ΔACH. Запишем пропорции сторон: 

\(\frac bc=\frac{b_c}b\)

Это значит, что отношение сторон, противолежащих прямому углу равно отношению сторон, лежащих напротив α. Выведем из пропорции следующее уравнение:

\((2)b^2=b_c\times c\)

Полученные равенства (1) и (2) доказывают теорему.

Теорема 2

Средним пропорциональным между проекциями катетов является высота, опущенная на гипотенузу из вершины угла в 90°, то есть при умножении отрезков ac и bc получается величина, равная квадрату высоты:

\(h^2=a_c\times b_c\)

Доказательство:

Поскольку ранее мы доказали подобия треугольников ΔABC∼ΔCBH и ΔABC∼ΔACH, то ΔCBH∼ΔACH. Используем этот факт для доказательства второй теоремы. Запишем пропорцию: 

\(\frac h{a_c}=\frac{b_c}h\)

Она значит, что отношение сторон, противолежащих углу (90°−α), равно соотношению сторон, противолежащих углу α. 

Выведем отсюда значение h:

\(h^2=a_c\times b_c\)

Теорема доказана.

Следствие

Гипотенуза разделена высотой на отрезки, соотношение которых равно отношению квадратов катетов. В виде формулы это свойство выглядит так:

\(\frac{a_c}{b_c}=\frac{a^2}{b^2}\)