АДСОРБЦИЯ
Поверхностная энергия стремится самопроизвольно уменьшиться. Это
выражается в уменьшении межфазной поверхности или поверхностного натяжения (s)
Вследствие этого стремления происходит адсорбция.
Адсорбция — процесс самопроизвольного
перераспределения компонентов системы между поверхностным слоем и объемной
фазой. Т.е. адсорбция может происходить в многокомпонентных системах, в слой
переходит тот компонент, который сильнее уменьшаетs.
Адсорбент — фаза определяющая форму
поверхности, более плотная, может быть твердой или жидкой.
Адсорбат — вещество которое
перераспределяется (газ или жидкость).
Десорбция — переход вещества из
поверхностного слоя в объемную фазу.
Количественно адсорбцию описывают
величиной Гиббсовской
адсорбции (избыток вещества в поверхностном слое по сравнению с его
количеством в объемной фазе, отнесенный к единице площади поверхности или
единице массы адсорбента)
(3.1)
Гi
-Гиббсовская адсорбция,
V -объем системы,
с -исходная концентрацияадсорбата ,
сi
— концентрация адсорбата в объеме,
S — площадь поверхности
раздела.
Все величины в (3.1) могут быть установлены экспериментально.
Гi может быть
меньше 0, если Co<Ci
Адсорбцию можно рассматривать как процесс превращения поверхностной
энергии в химическую.
Выведем соотношение между поверхностным натяжением и химическими
параметрами компонентов.
Если объем поверхностного слоя равен 0, то
dU=T dS + s dS
+ åmi dni(3.2)
т.к. внутр. энергия пропорциональна экстенсивным величинам, то:
U=T S + s S + åmi ni
полный дифференциал от тех же переменных запишется следующим образом:
dU=T dS + S dT + s dS
+S ds + åmi dni + å ni dm(3.3)
Подставляя dU из 3.2 в 3.3, получим:
S dT + s ds+ å ni dmi = 0 (3.4)
приТ=const:
sds + å ni dmi = 0(3.5)
3.4 и 3.5 — уравнения Гиббса для межфазной поверхности (поверхностного
слоя).
Все
экстенсивные величины поверхности зависят от площади поверхности , поэтому
удобнее относить эти параметры к единице площади поверхности. Разделив
уравнение 3.5 на площадь поверхности, получим:
=> (3.6)
Гi
— поверхностный избыток компонента i в поверхностном слое (по
сравнению с его равновесной концентрацией в объемной фазе), то есть величина
Гиббсовской адсорбции.
Уравнение 3.6 — фундаментальное адсорбционное уравнение Гиббса.
Это строгое термодинамическое соотношение, написанное для
многокомпонентнойсистемы. Однако,
практическое его использование неудобно. Оно,
например, не раскрывает зависимость поверхностного натяжения от адсорбции
конкретного вещества при постоянных химических потенциалах других веществ..
Единицы величины гиббсовской адсорбции определяются единицами химического
потенциала. Если потенциал отнесен к молю вещества, то величина адсорбции
выражается в молях на единицу площади.
Адсорбция конкретного вещества при постоянных химическихпараметрах других веществ:
Принимая во внимание , что mi = mio + RT ln ai,
mi и mio- равновесное и стандартное значения
химического потенциала адсорбата i, аi —
термодинамическая активность адсорбата, dmi = RTd ln ai,получим
для Гиббсовской адсорбции:
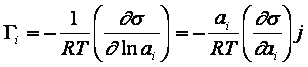 (3.7)
(3.7)
3.7. применяют только тогда, когда можно использовать концентрации
вместо активностей и пренебречь изменениями концентраций других веществ при
изменении концентрации одного вещества. Этим условиям удовлетворяет разбавленный
раствор относительно данного компонента. В таком растворе при изменении
концентрации растворенного вещества практически не изменяется концентрация
растворителя. Поэтому для растворенного вещества уравнение 3.7 переходит в
широко используемые адсорбционные уравнения Гиббса для неэлектролитов и
электролитов
(3.8)
Для электролитов:
(3.9)
Изотерма адсорбции Фрейндлиха
Теоретические представления, развитые Ленгмюром и Поляни, в значительной степени идеализируют и упрощают истинную картину адсорбции. На самом деле поверхность адсорбента неоднородна, между адсорбированными частицами имеет место взаимодействие, активные центры не являются полностью независимыми друг от друга и т.д. Все это усложняет вид уравнения изотермы. Г. Фрейндлих показал, что при постоянной температуре число молей адсорбированного газа или растворенного вещества, приходящееся на единицу массы адсорбента (т.н. удельная адсорбция x/m), пропорционально равновесному давлению (для газа) или равновесной концентрации (для веществ, адсорбируемых из раствора) адсорбента, возведенным в некоторую степень, которая всегда меньше единицы:
Показатель степени n и коэффициент пропорциональности а в уравнении Фрейндлиха определяются экспериментально. Логарифмируя уравнения, получаем:
УРАВНЕНИЕ ГЕНРИ, ФРЕЙНДЛИХА, ЛЕНГМЮРА
Для
описания процесса адсорбции, помимо фундаментального уравнения адсорбции
Гиббса, применяют ряд других аналитических уравнений, которые называются по
имени их авторов.
При
незначительном заполнении адсорбента адсорбатом отношение концентрации вещества
в адсорбционном слое и в объеме стремится к постоянному значению, равному кГ:
Г(А) = кГс (3.10)
Это
уравнение характеризует изотерму адсорбции при малых концентрациях адсорбата
(рис.3.1, участок 1) и является аналитическим выражением закона Генри. Коэффициент кГ не зависит от концентрации
и представляет собой константу распределения, характеризующую распределение
вещества в адсорбционном слое по отношению к его содержанию в объемной фазе.
Уравнение Генри соблюдается приближенно, но это приближение достаточно для
практики.
В
более общем виде зависимость адсорбции от концентрации адсорбата можно
определить с помощью уравнения
Фрейндлиха.
Г(А) = кс1/n(3.11)
к, n
-коэффициенты.

Это
уравнение было получено на основе результатов обработки опытных данных по
адсорбции поверхностно-активных веществ при концентрации адсорбата с = 1, к =
Г. Коэффициент к численно равен величине адсорбции при с = 1.Коэффициент n
характеризует отличие участка изотермы адсорбции (рис.3.1, участок 2) от
прямой.
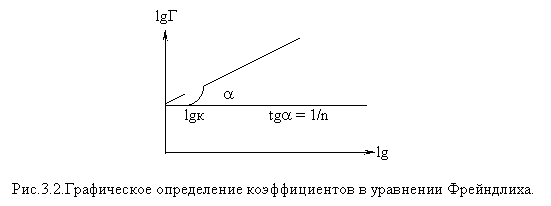
Коэффициенты
в уравнении Фрейндлиха можно
определить графически, если прологарифмировать уравнение 3.11:
lgГ(А) = lgк+n1/nlgс(3.12)
Графическая
зависимость приведена на рис.3.2.
Изотерма
адсорбции, которая соответствует уравнению
Фрейнлиха (рис.3.1, участок 2).

В основу
теории положены кинетические представления о процессе адсорбции в условиях
равновесия.
Представим
единицу площади на границе раздела фаз. Если молекула адсорбата занимает в
поверхностном слое площадь В, а число его молекул — n,
то nВ
— это площадь, которая приходится на все молекулы в расчете на единицу площади
адсорбционного слоя. Поверхность, свободная от молекул адсорбата = (1 — nВ),
свободная площадь определяет возможность дальнейшего протекания адсорбции.
vа = кас(1 — nВ)
— скорость адсорбции(3.13)
vд=каnВ
— скорость десорбции(3.14)
ка
и кд — константы адсорбции и десорбции.
В
условиях равновесия скорости прямого и обратного процессов равны,
следовательно, обозначив константу равновесия через b, получим:
b = ка/кд
= (3.15)
Константа
равновесия связана со значением изобарно-изотермического потенциала:
DG=RТlnb
Проведем
вспомогательные преобразования уравнения 3.15:
1/bс
= (1 — nВ)/nВ=1/nВ- 1,
выразим
число молекул адсорбата:
n = (1/В)*bс/(1
+ bс)(3.16)
В
случае предельной адсорбции вся площадь занята молекулами:
nВ=1, n- число молекул в
насыщенном слое.
Степень
насыщения q адсорбционного слоя:
q=nn(3.17)
в
процессе адсорбции:
<q<1.
n = Г(А)NА,
n= Г(А)NА, тогда:
Г(А) = Г(А)*bс(1 + bс)(3.18)
3.18.
— уравнение Ленгмюра (рис.3.1,
участок 3.)
Теория объемного заполнения микропор (ТОЗМ).
М.М.Дубинин с сотрудниками разработали теорию равновесной адсорбции вещества на микропористых адсорбентах; термодинамические аспекты этой теории разработаны Б.П. Берингом и В.В. Серпинским. Согласно T03М адсорбция характеризуется объемным заполнением адсорбционного пространства микропор без последовательного образования слоев. Основным геометрическим параметром микропористого адсорбента является объем микропор, а не площадь их поверхности. Рассматриваемая теория является термодинамической, и в основу ее положены такие термодинамические функции, как свободная энергия, энтропия и энтальпия.
Если для вычисления изменения этих функций в качестве стандартного состояния принять объемную жидкую фазу адсорбата, находящуюся в равновесии с ее насыщенным паром при давлении рs, или летучести fs, то дифференциальная максимальная молярная работа адсорбции А равна по величине, но противоположна по знаку, изменению свободной энергии Гиббса DG
В уравнении (7.4) и всех последующих выражениях неидеальность газовой фазы легко учесть, вводя летучесть вместо давления. Дифференциальная молярная энтропия адсорбата DS, отсчитываемая от уровня энтропии, соответствующего адсорбируемому веществу в виде жидкости при температуре опыта:
Изменение энтальпии DI равно по абсолютному значению дифференциальной теплоте адсорбции q:
DI = — q = DG+ T D S= — А + T( ¶ A / ¶ T)a. (7.6)
Используя известный в математической статистике закон распределения Вейбулла, М.М. Дубинин и В.А. Астахов получили уравнение изотермы адсорбции в аналитической форме:
где q — степень заполнения объема микропор; a — предельная величина адсорбции при температуре Т; Е — характеристическая свободная энергия адсорбции; n — безразмерный параметр (при адсорбции на углеродных адсорбентах n = 2, на микропористых n = 3, на цеолитах n = 3. 6).
Зависимость А = E f(q,n) названа характеристической кривой.
Основные исходные положения ТОЗМ: постоянство объема адсорбционного пространства, т.е. объема микропор адсорбента; температурная независимость (инвариантность) характеристической кривой (следствием является постоянство параметров Е и n); подобие характеристических кривых для различных паров.
Первое исходное положение ТОЗМ позволяет определить предельную величину адсорбции а при любой температуре Т, если она определена при стандартной температуре Т по уравнению а = а 0 ехр,
где а 0 — предельная величина адсорбции при стандартной температуре Т (обычно принимают равной температуре тpoйной точки); a. — термический коэффициент предельной адсорбции, который можно вычислить по физическим константам адсорбата.
Температурная инвариантность характеристической кривой означает, что зависимость дифференциальной молярной работы адсорбции от степени заполнения q одна и та же для всех температур данной системы адсорбат—адсорбент. Термодинамически установлена нижняя граница строгого соблюдения температурной инвариантности q = 0,15. 0,20. При степени заполнения q 2 /b 2 )[lg(ps/p)] 2 >, (7.8)
где В = 4,574/Ё 2 — константа.
Дальнейшее развитие ТОЗМ было направлено на область адсорбции газов при температурах Т > Тк. Если химический потенциал адсорбтива в стандартном состоянии определятся некоторым параметром Z, а не давлением р, изменение энергии Ги66ca
В этом случае уравнение изотермы ТОЗМ имеет вид
При условии линейности изостер адсорбции в интервале температур Т Тк, найдем параметр Z, определяющий стандартное состояние газа при Т > Тк :
, (7.10)
где k и с — константы уравнения изостеры адсорбции ln р = k — с/Т.

Полученные приближенные уравнения (7.9) и (7.10) позволяют рассчитать изотерму адсорбции вещества при наличии минимальной экспериментальной информации для o6ласти температур Т > Тк (необходима только одна точка изотермы).

Последнее изменение этой страницы: 2019-03-22; Просмотров: 410; Нарушение авторского права страницы
Константы адсорбции в уравнениях ленгмюра и генри
Небольшая предыстория . В ходе изучения ПАВ американский химик и физик Ирвинг Ленгмюр выдвинул и математически обосновал идею об особом строении адсорбционных слоев. Он рассматривал ненасыщенный слой как двухмерный газ. По мере того как концентрация ПАВ увеличивается, происходит процесс, аналогичный конденсации двухмерного газа – молекулы образуют двухмерную пленку, которую Ленгмюр рассматривал как двухмерную жидкость. Если концентрация ПАВ в растворе неограниченно возрастает, то наступает момент предельного насыщения адсорбционного слоя, который приобретает вид частокола, так как предполагается, что слой имеет толщину, соответствующую длине адсорбированной молекулы. При этом адсорбция достигает предела. Эта теория была названа теорией мономолекулярного слоя, или монослоя.
Теория Ирвинга Ленгмюра(1914-1918) явилась фундаментальным вкладом в учение об адсорбции. Она позволяет учесть наиболее сильные отклонения от закона Генри, связанные с ограниченностью поверхности адсорбента. Ограниченность этого параметра приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации распределяемого вещества.
Теория мономолекулярной адсорбции основывается на следующих положениях:
1) Адсорбция является локализованной (происходит на адсорбционных центрах).
2) Адсорбция происходит не на всей поверхности адсорбента, а на активных центрах, которыми являются выступы либо впадины на поверхности адсорбента. Активные центры считаются независимыми (т.е. один активный центр не влияет на адсорбционную способность других), и тождественными.
3) Каждый активный центр способен взаимодействовать только с одной молекулой адсорбата; в результате на поверхности может образоваться только один слой адсорбированных молекул.
4) Процесс адсорбции находится в динамическом равновесии с процессом десорбции.
На основании этих положений можно получить уравнение изотермы адсорбции. Скорость адсорбции из газовой фазы V ад (т.е число молекул, адсорбированных за единицу времени) пропорциональна давлению газа и числу свободных центров на поверхности твердого тела. Если общее число центров a ∞ ,а при адсорбции оказывается занятыми a центров, то число центров, остающийся свободными равно ( a ∞ — a ). Поэтому:
Адсорбция динамически уравновешена процессом десорбции. Скорость десорбции пропорциональна числу адсорбированных молекул:
Переобозначаем k ад k дес = b (где b –это константа адсорбированного равновесия),получаем
I — почти горизонтальный участок, который соответствует большим концентрациям, отвечает поверхности адсорбента, полностью насыщенным адсорбтивом. Величина удельной адсорбционной способности в этом случае не зависит от равновесной концентрации адсорбтива в растворе, что свидетельствует об образовании на поверхности мономолекулярного слоя.Описывается уравнением Генри:
II — соответствует промежуточным степеням заполнения поверхности.Описывается уравнением Фрейндлиха
III -почти все адсорбционные центры уже заняты и свободных центров на поверхности почти нет.
Уравнение Ленгмюра содержит два параметра, характеризующих адсорбцию. Это константа адсорбционного равновесия b и величина предельной адсорбции a ∞ , соответствующая полной полному заполнению поверхности мономолекулярным слоем адсорбата .
Для определения численных значений a ∞ и b уравнение Ленгмюра можно представить в виде:
С помощью линеаризации уравнения Ленгмюра можно определить предельную величину адсорбции a ∞ , соответствующую полному мономолекулярному покрытию адсорбента молекулами адсорбата.
Экспериментальное определение a ∞ позволяет рассчитать удельную поверхность адсорбента S уд:
где NA — постоянная Авагадро, W — площадь, приходящаяся на единичную молекулу адсорбата в мономолекулярном слое.
Однако,следует отметить некоторое развитие в положениях теории:
Во-первых,адсорбционные центры таки могут иметь разную энергию.
И в этом случае a ∞ будет рассчитываться как сумма всех различных центров:
Во-вторых,молекулы могут взаимодействовать между собой.
И наконец,на один адсорбционный центр может приходиться несколько молекул.
Т.е молекула первого слоя может являться вторичным центром.Это положение описывает теория о полимолекулярной адсорбции(теория БЭТ),но это уже совсем другая история ![]()
1.Левченко С.И. // Физическая и коллоидная химия.4.1.4Поверхностные явления и адсорбция.
2.Пальтиель Л.Р. // Коллоидная химия.8.Теория мономолекулярной адсорбции Ленгмюра
3. Журнал «Горизонт чистоты» //Теоретические основы клининга.2.5. Адсорбция ПАВ на границе раздела «жидкость-газ»
Теория полимолекулярной адсорбции уравнение фрейндлиха
В большинстве случаев реальная поверхность твердого тела не вполне однородна энергетически; адсорбция, как правило, не является строго локализованной; адсорбированные молекулы практически всегда взаимодействуют между собой; наконец, стехиометрия может нарушаться, вследствие чего адсорбция не будет ограничена образованием одного слоя. Поэтому реальные изотермы адсорбции всегда отклоняются от изотермы Ленгмюра. Еще самим Ленгмюром было показано, что если адсорбционные центры считать энергетически неоднородными, то суммарная адсорбция на всех центрах будет выражена следующим уравнением:
где i — количество групп одинаковых центров.
Брунауэр, Эммет и Теллер отказались от второго допущения Ленгмюра, приводящего к мономолекулярной адсорбции. Для случая, когда температура адсорбтива ниже критической (то есть, это еще пар) они разработали теорию полимолекулярной адсорбции. После анализа многочисленных реальных изотерм адсорбции ими была предложена их классификация на основе выделения пяти основных типов изотерм.
Изотермы типа I отражают мономолекулярную адсорбцию. Изотермы типа II и III обычно связывают с образованием при адсорбции многих слоев, то есть, с полимолекулярной адсорбцией. Приче м, в случае II взаимодействие адсорбент — адсорбат сильнее взаимодействия адсорбат — адсорбат, а в случае III — наобор от. Изотермы типа IV и V отличаются тем, что для них характерна конечная адсорбция при приближении давления пара к давлению насыщения ps. Изотермы типа II и III характерны для адсорбции на не пористом адсорбенте, а типа IV и V — на пористом твердом теле. Все пять типов изотерм адсорбции описываются теорией полимолекулярной адсорбции “БЭТ”, названной так по начальным буквам фамилий ее авторов.
Теория БЭТ сохраняет ленгмюровские представления о динамическом характере адсорбции. Адсорбция считается полислойной. Молекулы первого слоя адсорбируются на поверхности адсорбента в результате межмолекулярного взаимодействия адсорбент — адсорбат. Каждая адсорбированная молекула первого адсорбционного слоя может, в свою очередь, являться центром адсорбции молекул второго слоя и т.д. Так формируются второй и последующие сорбционные слои. Теплота адсорбции в первом слое q1 определяется взаимодействием адсорбат — адсорбент, во всех последующих слоях — взаимодействием адсорбат — адсорбат. Поэтому теплота адсорбции во всех слоях, начиная со второго, равна теплоте конденсации λ. Второй и последующие адсорбционные слои могут начинать образовываться и при незавершенном первом слое, как это показано на рисунке:
Составив уравнение адсорбционного равновесия для каждого слоя и просуммировав их, авторы теории БЭТ получили уравнение для полислойной адсорбции:
В приведенном уравнении АМ — емкость монослоя, С — константа, равная е (q1− λ) / RT . При малых относительных давлениях, когда р как частный случай уравнения БЭТ. В случаях, когда q1 > λ , т.е. энергия взаимодействия адсорбент — адсорбат больше энергии взаимодействия адсорбат — адсорбат, изотерма адсорбции выпукла и относится к типу II или IV. Если же энергия взаимодействия адсорбат — адсорбат больше теплоты адсорбции ( λ > q1 ), то изотерма адсорбции вогнута и относится к типу III или V.
Уравнение изотермы адсорбции БЭТ широко используется для определения величины удельной поверхности адсорбентов. Изотерма адсорбции выражается прямой линией, отсекающей на оси ординат отрезок, равный 1 / АМ С , а тангенс угла ее наклона к оси абсцисс равен (С − 1) / АМ С.
Из этих значений можно найти величину АМ, а зная ее, рассчитать по уравнению удельную поверхность адсорбента. Стандартной методикой для определения удельной поверхности адсорбентов принято считать измерение изотермы адсорбции азота при 77 К. В этом случае wо = 0.162 нм 2 .
Взаимодействие частиц в адсорбционном слое и классификация изотерм адсорбции
Одним из опорных пунктов теории Ленгмюра является константа отсутствия взаимодействия частиц адсорбата в адсорбционном слое, Однако ленгмюровская адсорбция является лишь частным случаем в многообразном мире адсорбционных процессов. На рис. 9.4 показаны различные формы изотерм адсорбции из разбавленных растворов.
Рисунок 9.4 ‒ Формы изотерм адсорбции
Исходя из формы начального участка были выделены четыре характерных класса изотерм (S, L, H, C). Деление изотерм на отдельные типы внутри каждого класса связано с последующим изменением их формы при наиболее высоких концентрациях. Класс L (класс Ленгмюра) является наиболее общим. Изотермы типа L2 достигают насыщения, дальнейшая адсорбция выше этого уровня дает изотерму типа L3. Если достигается второе плато, то имеем дело с изотермой L4. Для изотерм типа L5 характерно наличие максимума. Максимум отражает изменение состояния вещества в растворе — например, ассоциацию молекул при определенной концентрации. Сходный, хотя и не столь полный, набор типов изотерм получен и для других классов.
Начальный участок изотерм S — класса выгнут относительно оси концентраций, однако далее часто следует точка перегиба, что и придает изотерме характерную S -обратную форму.
Изотермы класса Н (высокое сродство – higf) наблюдается при чрезвычайно сильной адсорбции при очень низких концентрациях; они пересекаются с осью ординат. Изотермы класса С (constant) имеют начальный линейный участок, что указывает на постоянное распределение растворенного вещества между раствором и адсорбентом (постоянная скорость адсорбции).
Теоретический анализ различных типов изотерм адсорбции позволяет получить много полезной информации о механизме адсорбции
При этом следует принимать во внимание величину энергии активации процесса удаления молекул адсорбата с поверхности адсорбента. Если взаимодействие между адсорбированными молекулами пренебрежимо мало, энергия активации не зависит от степени заполнения поверхностиf a это приведет к изотерме типа L или Н
Если сила взаимодействия между адсорбированными молекулами больше силы взаимодействия между растворенным веществом и адсорбентом, энергия активации возрастает и адсорбция описывается изотермой типа S. В этом случае молекулы растворенного вещества стремятся расположиться на поверхности в виде цепей.
Изотермы типа Н наблюдаются в тех случаях, когда имеет место хемосорбция.
Изотерма типа С характерна для адсорбции на микропористых адсорбентах и соответствует таким условиям, при которых число адсорбционных центров остается постоянным в широкой области концентраций. По мере заполнения одних центров появляются новые, и доступная для адсорбции поверхность увеличивается пропорционально количеству адсорбированного вещества.
ПОВЕРХНОСТНАЯ АКТИВНОСТЬ
В
уравнении Гиббса- поверхностная
активность — характеристика веществ при адсорбции.
(3.19)
Для
неэлектролитов:
(3.20)
Для
электролитов:
(3.21)
Размерность:
Дж м3d-2/мольd (для электролитов)
Дж
м/моль (для неэлектролитов)
Физический
смысл:
g — сила, удерживающая вещество на поверхности,
рассчитанная на единицу Г.
g может быть больше 0 и меньше 0.
Если с увеличением концентрации веществаповерхностное натяжение на границе раздела фаз уменьшается, то такое
вещество называется
поверхностно-активным:
g > 0,< 0, Г
> 0
Вещества
увеличивающиеповерхностное натяжение — поверхностно-инактивные:
g < 0, > 0, Г
< 0
Г < 0 — это значит концентрация адсорбируемого
вещества в объеме больше, чем в поверхностном слое. Термин “поверхностно-активные
вещества”(ПАВ) обычно применяют к специфическимвеществам, обладающим очень большой поверхностной активностью по
отношению к воде, что является следствием их особого строения. Молекулы ПАВ имеют
неполярную (углеводородную) часть и полярную часть из функциональных групп —
COOH, — NH2, — OH, -O-, -SO2OH и др. Углеводородные
радикалы выталкиваются из воды на поверхность (Г>0). ПАВ типа мыл уменьшают
поверхностное натяжение водыс 72 до
30мДж/м2. Это значит, что в
поверхностном слое концентрация ПАВ в 3 104 раз превышает
концентрацию в объеме.































