Чистый сдвиг

Ползучесть анизотропного грунта при чистом сдвиге

Проведены исследования ползучести анизотропного грунта при чистом сдвиге в стабилометре. Чистый сдвиг создавался следующим образом: вначале образец глинистого грунта обжимался в стабилометре гидростатическим напряжением, а после затухания деформации к нему добавлялось вертикальное давление при одновременном уменьшении бокового на величину в два раза меньше вертикального. При этом изменение формы образца происходило без изменения объема. Изменение объема образца контролировалось внутри стабилометра малогабаритной месдозой, изготовленной авторами на основе кремниевых тензорезисторов. При испытании измерялись деформации ползучести скелета грунта во времени, начиная от условно-мгновенной до длительной. Мгновенная деформация определялась в условиях компрессии с замером индикаторов перемещения с помощью видеосъемки. Стабилометр использовался как компрессионный прибор, т. е. образец испытывался без возможности бокового расширения. Длительная деформация образца во времени фиксировалась до п…

Еще термины по предмету «Механика»

Вековое уравнение (уравнение частот)

многочленное уравнение для разрешённых частот гармонических колебаний при решении задачи малых (линейных) колебаний.

Внецентренное растяжение

стержень нагружен двумя одинаковыми по величине растягивающими силами, направленными в противоположные стороны вдоль прямой, не проходящей через центры тяжести поперечных сечений.

• Сдвиг

• Прочность при сдвиге (предел прочности при сдвиге, прочность на сдвиг)

• Сдвиг содержания

• Линия сдвига

• Сдвиг ветра

• Волна сдвига

• Антициклонический сдвиг

• Структурный сдвиг

• Сдвиг частоты

• Демографический сдвиг

• Модуль сдвига

• Напряжение сдвига

• Плоскость сдвига

• Скорость сдвига

• Сдвиг штампа

• Сдвиг к риску

• Сдвига оператор

• Сдвиг рамки

• Операции сдвига ( « и » )

• Деформация сдвига

Прочность при чистом сдвиге анизотропных материалов

Приведены результаты численного эксперимента по исследованию напряженного состояния анизотропного материала при испытаниях на чистый сдвиг. В качестве анизотропного материала были выбраны древесно-стружечные плиты. Древесно-стружечные плиты композиционный неоднородный ортотропный материал, поэтому использование его в качестве конструкционного материала (мебельные конструкции, строительный материал) требует проведения прочностных расчетов в условиях сложного напряженного состояния и использования соответствующих критериев прочности. С целью определения прочности древесины при чистом сдвиге ранее была разработана методика испытаний, включающая образец сложной формы и приспособление для нагружения этого образца. Для оценки напряжений в рабочей части образца были проведены исследования на модели из оптически активного изотропного материала, которые дали положительный результат. При оценке влияния анизотропии на распределение напряжений в анизотропной среде целесообразно использовать ана…

Геометрические характеристики плоских сечений

Площадь
:
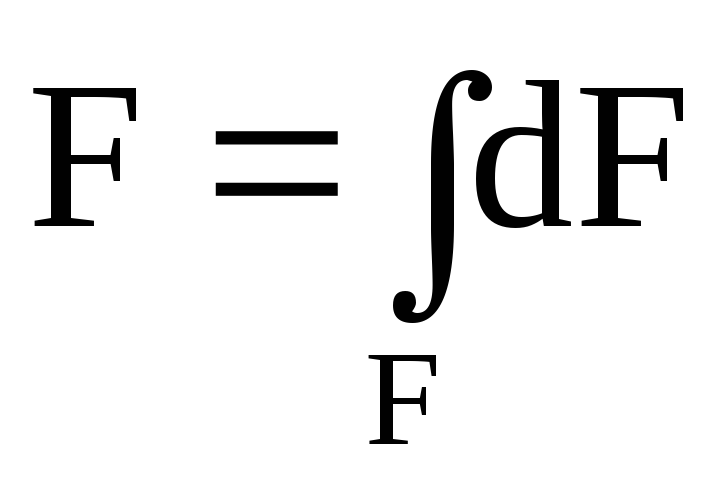,dF
— элементарная площадка.

Статический
момент элемента площади
dF

относительно оси 0x
— произведение элемента площади на
расстояние «y»
от оси 0x:
dS x
= ydF

Просуммировав
(проинтегрировав) такие произведения
по всей площади фигуры, получаем
статические
моменты

относительно осей y
и x:
;

.

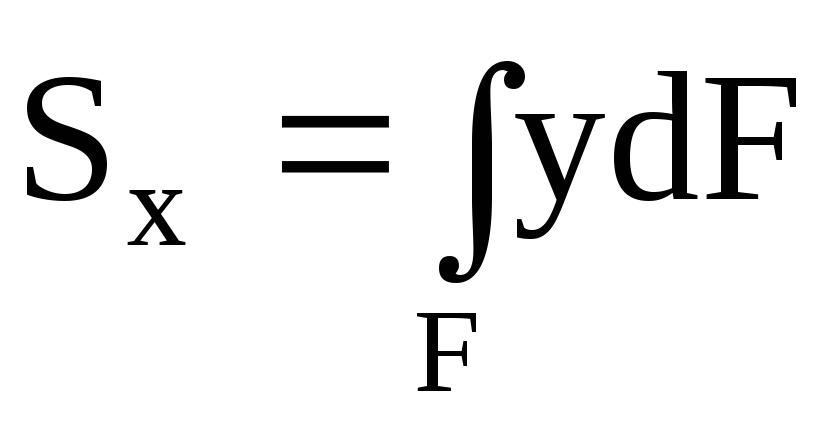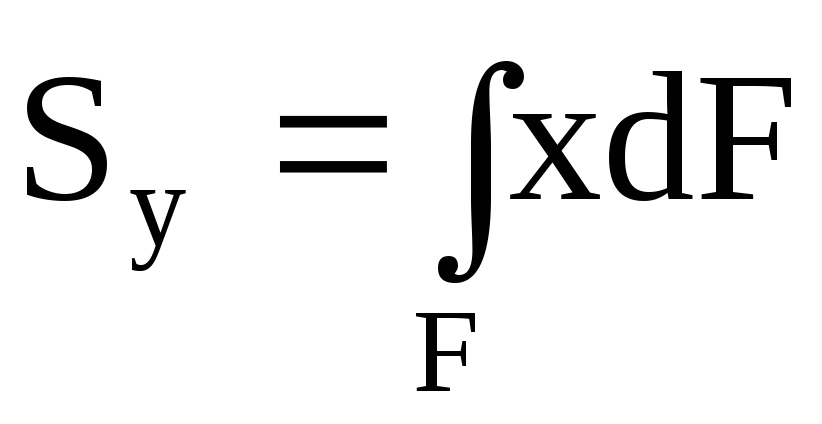
Координаты
центра тяжести

.
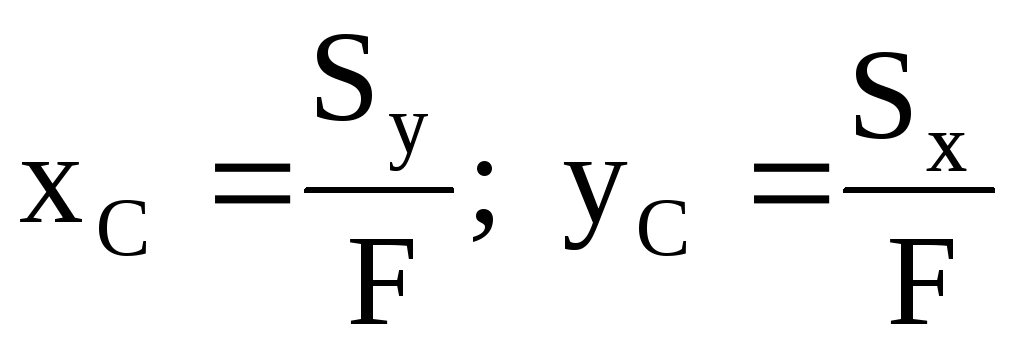Статические моменты относительно
центральных
осей
(осей,
проходящих через центр тяжести сечения)
равны нулю. При вычислении статических
моментов сложной фигуры ее разбивают
на простые части, с известными площадями
F i
и координатами центров тяжести x i ,
y i .Статический
момент площади всей фигуры = сумме
статических моментов каждой ее части:
.

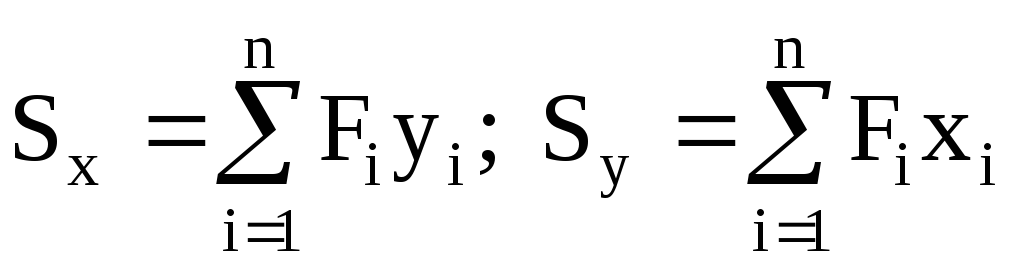Координаты
центра тяжести сложной фигуры: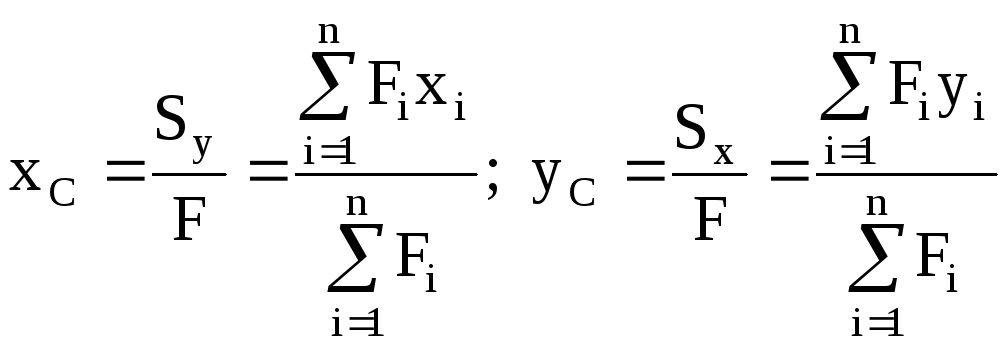

М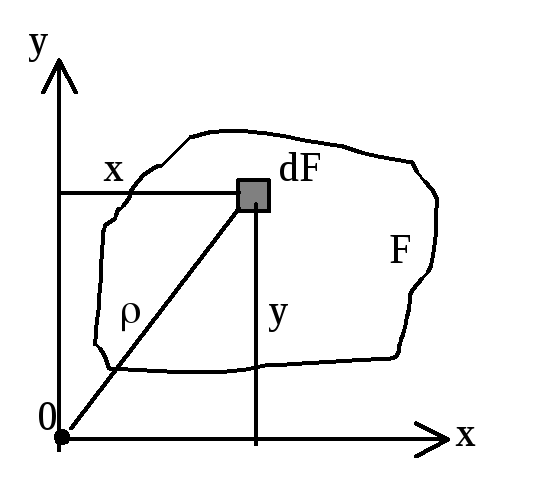оменты
инерции сечения

Осевой

(экваториальный) момент
инерции сечения

— сумма произведений элементарных
площадок dF
на квадраты их расстояний до оси.

;

.

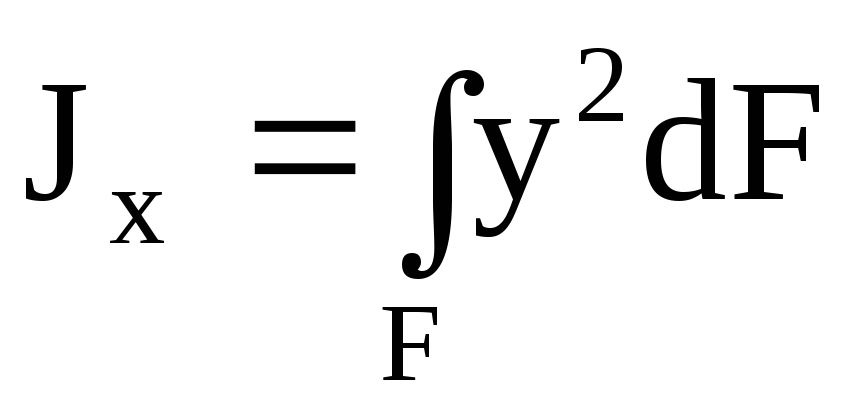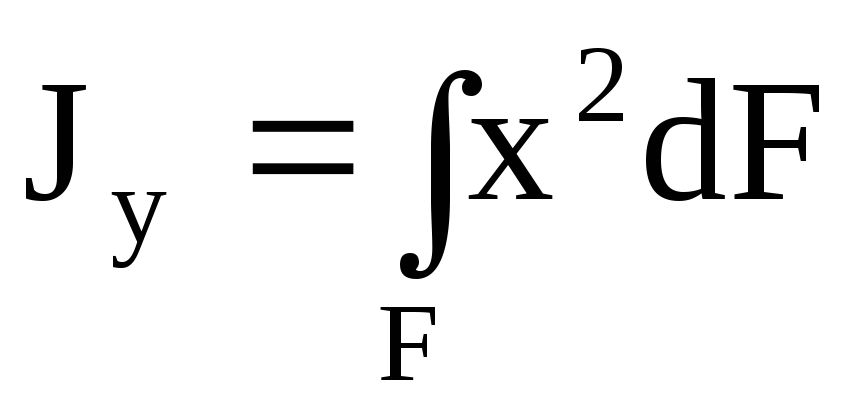
Полярный
момент инерции сечения

относительно
некоторой точки (полюса) — сумма
произведений элементарных площадок на
квадраты их расстояний от этой точки.
;
.
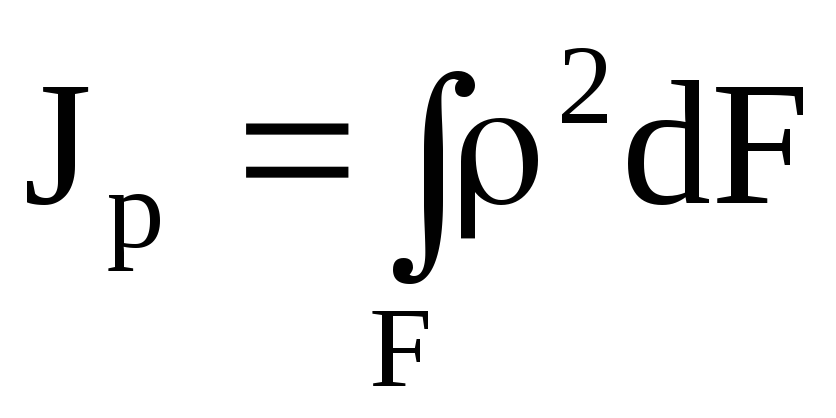J y
+ J x
= J p
.

Центробежный
момент инерции сечения

— сумма произведений элементарных
площадок на их расстояния от двух взаимно
перпендикулярных осей.
.

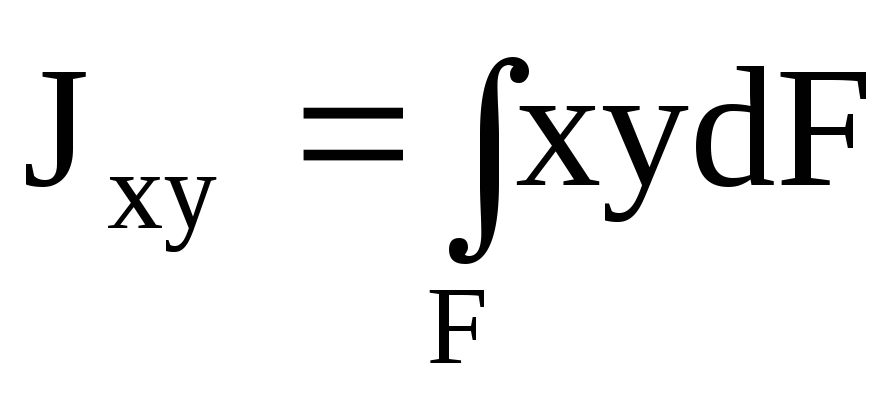Центробежный
момент инерции сечения относительно
осей, из которых одна или обе совпадают
с осями симметрии, равен нулю.

Осевые
и полярные моменты инерции всегда
положительны, центробежные моменты
инерции могут быть положительными,
отрицательными или равными нулю.

Момент
инерции сложной фигуры равен сумме
моментов инерции составных ее частей.

Моменты инерции
сечений простой формы

Прямоугольное
сечение

Круг

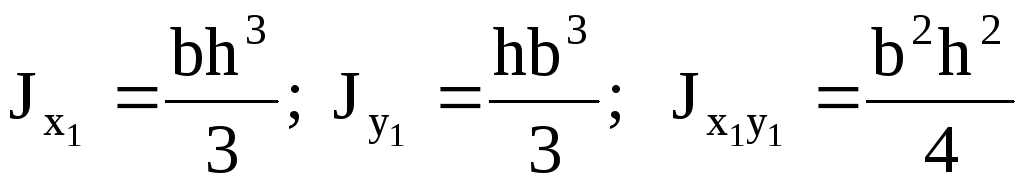
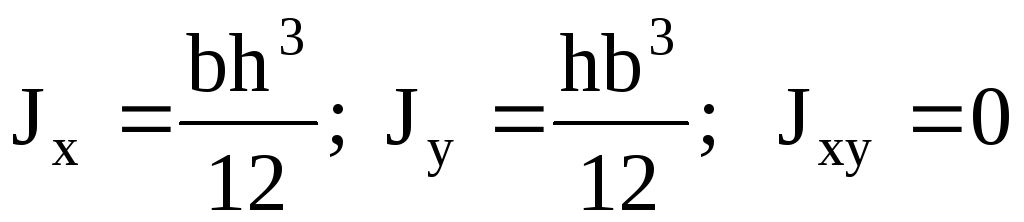
Кольцо

Т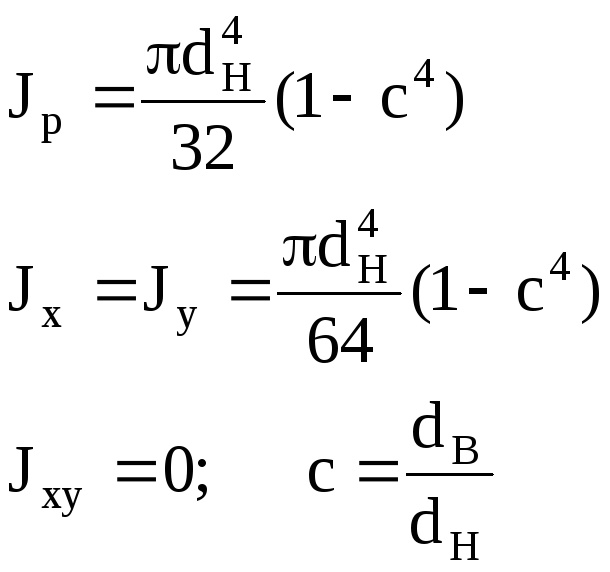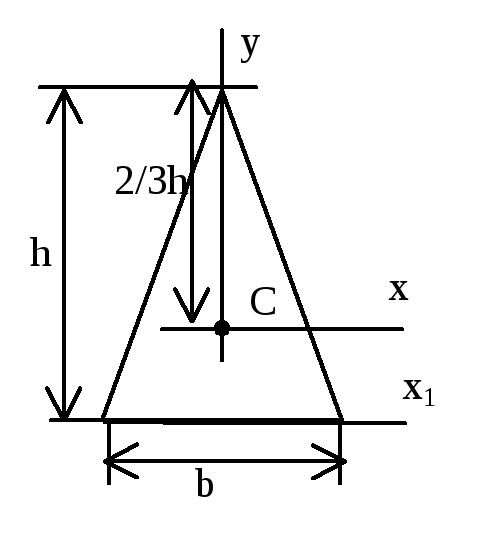реугольник

р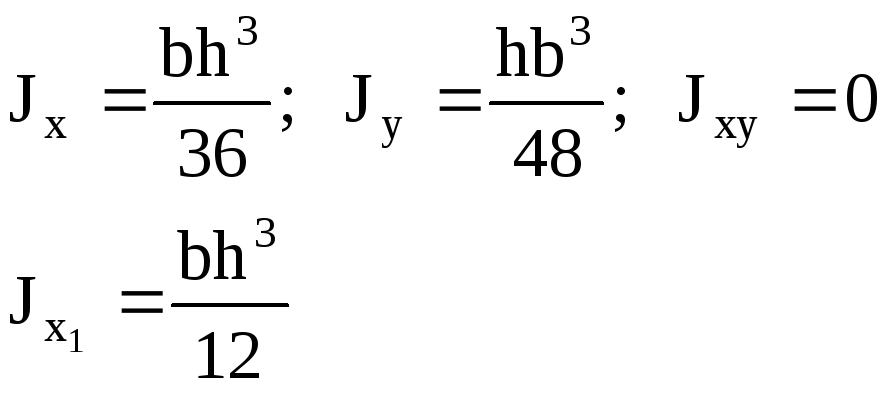авнобедренный

Прямоугольный

т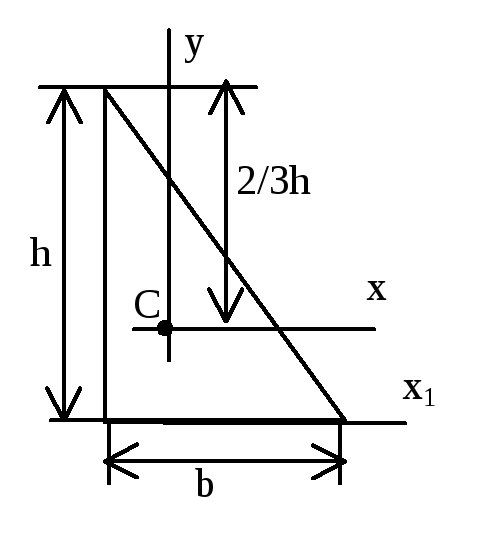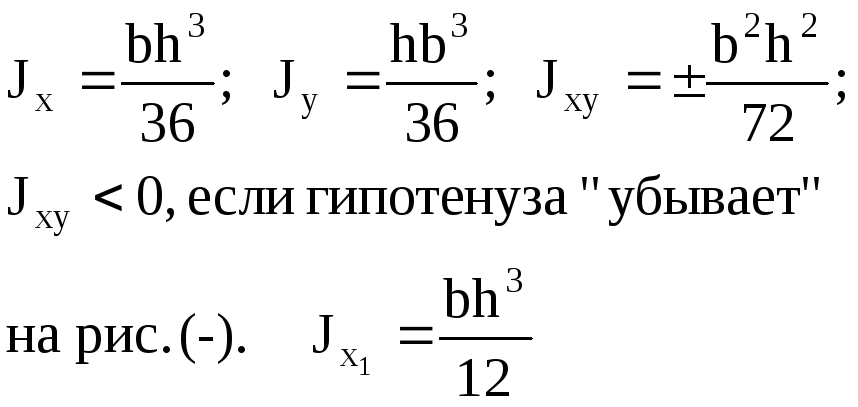реугольник

Четверть
круга

J y =J x =0,055R 4

J xy =0,0165R 4

на
рис. (-)

J x 0 =0,0714R 4

J y 0 =0,0384R 4

Полукруг

Моменты
инерции стандартных профилей находятся
из таблиц сортамента:

Двутавр

Швеллер

Уголок

М

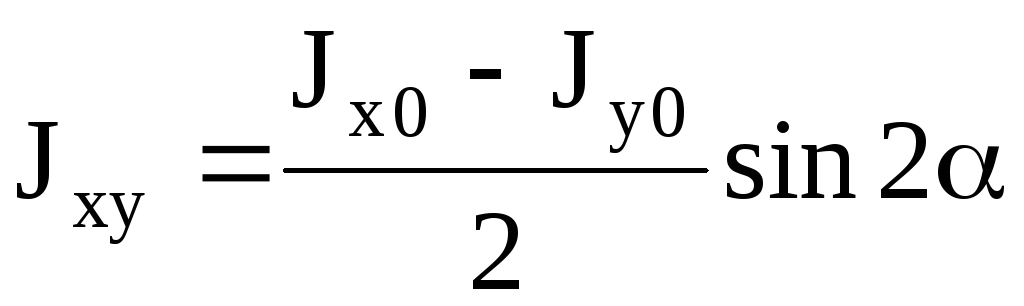
оменты инерции относительно
параллельных осей
:

J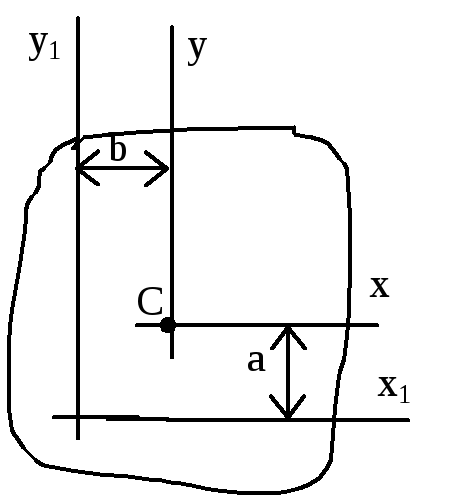 x1 =J x
+ a 2 F;

J y1 =J y
+ b 2 F;

момент
инерции относительно любой оси равен
моменту инерции относительно центральной
оси, параллельной данной, плюс произведение
площади фигуры на квадрат расстояния
между осями. J y 1 x 1 =J yx
+ abF;
(«a»
и «b»
подставляют в формулу с учетом их знака).

Зависимость
между моментами
инерции при повороте осей
:

J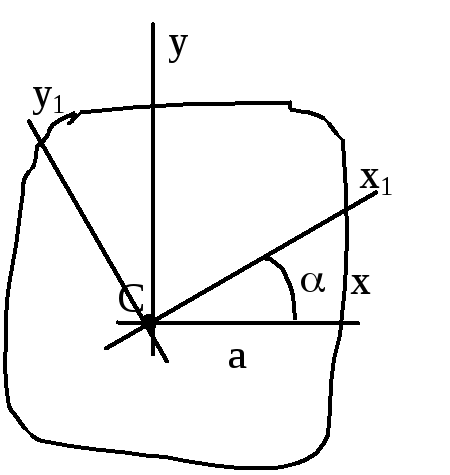 x 1 =J x cos 2 
+ J y sin 2 
— J xy sin2;
J y 1 =J y cos 2 
+ J x sin 2 
+ J xy sin2;

J x1y1 =(J x
— J y)sin2
+ J xy cos2
;

Угол
>0,
если переход от старой системы координат
к новой происходит против час.стр. J y 1
+ J x 1 =
J y
+ J x

Главные
моменты инерции

.

Экстремальные
(максимальное и минимальное) значения
моментов инерции называются главными
моментами инерции

.

Оси, относительно которых осевые моменты
инерции имеют экстремальные значения,
называются главными
осями инерции
.
Главные оси инерции взаимно перпендикулярны.
Центробежные моменты инерции относительно
главных осей = 0, т.е. главные оси инерции
— оси, относительно которых центробежный
момент инерции = 0. Если одна из осей
совпадает или обе совпадают с осью
симметрии, то они главные. Угол,
определяющий положение главных осей:
,
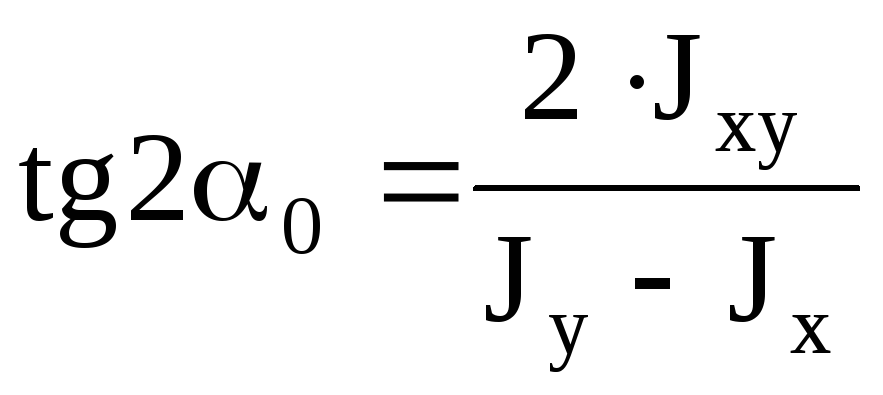если 0 >0

оси поворачиваются против час.стр. Ось
максимума всегда составляет меньший
угол с той из осей, относительно которой
момент инерции имеет большее значение.
Главные оси, проходящие через центр
тяжести, называются главными
центральными осями инерции
.
Моменты инерции относительно этих осей:

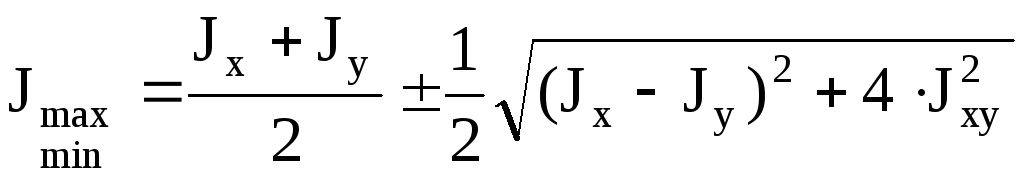
J max
+ J min =
J x
+ J y .
Центробежный момент инерции относительно
главных центральных осей инерции равен
0. Если известны главные моменты инерции,
то формулы перехода к повернутым осям:

J x 1 =J max cos 2 
+ J min sin 2 ;
J y 1 =J max cos 2 
+ J min sin 2 ;
J x 1 y 1 =(J max
— J min)sin2;

Конечной
целью вычисления геометрических
характеристик сечения является
определение главных центральных моментов
инерции и положения главных центральных
осей инерции. Радиус
инерции
—
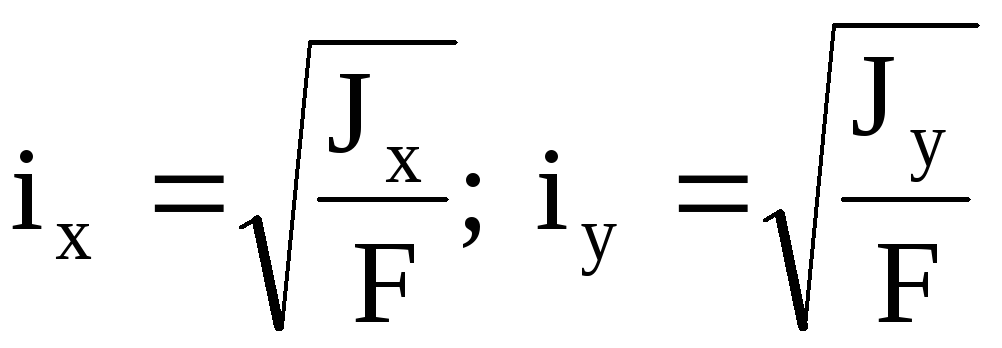;J x =Fi x 2 ,
J y =Fi y 2 .

Если
J x
и J y
главные моменты инерции, то i x
и i y
— главные
радиусы инерции
.
Эллипс, построенный на главных радиусах
инерции как на полуосях, называется
эллипсом
инерции
. При
помощи эллипса инерции можно графически
найти радиус инерции i x 1
для любой оси х 1 .
Для этого надо провести касательную к
эллипсу, параллельную оси х 1 ,
и измерить расстояние от этой оси до
касательной. Зная радиус инерции, можно
найти момент инерции сечения относительно
оси х 1:
.
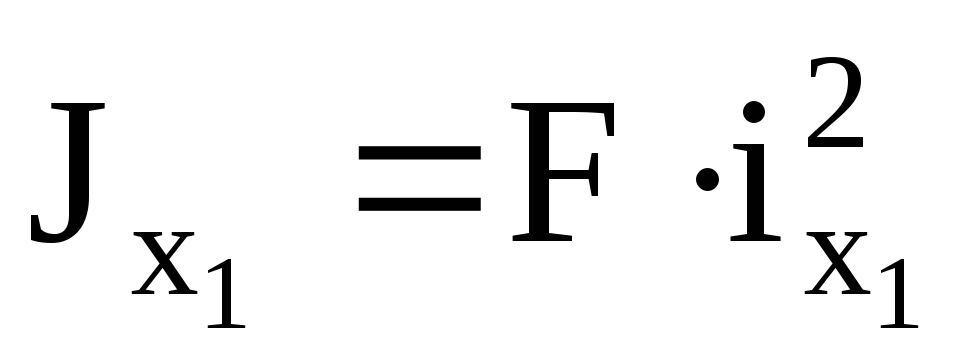Для сечений, имеющих более двух осей
симметрии (например: круг, квадрат,
кольцо и др.) осевые моменты инерции
относительно всех центральных осей
равны между собой, J xy =0,
эллипс инерции обращается в круг инерции.