Сферический треугольник

Решение прямоугольных и четвертных сферических треугольников

Прямоугольные и четвертные сферические треугольники являются частным случаем косоугольных сферических треугольников.

Прямоугольным сферическим треугольником называется такой сферический треугольник, у которого один из углов равен 90°.

Четвертным сферическим треугольником называется такой сферический треугольник, у которого одна из сторон равна 90°.

К этим треугольникам применимы все правила и алгоритмы решения косоугольных сферических треугольников.

Прямоугольные треугольники можно решать по основным формулам сферической тригонометрии. Так как один из углов равен 90°, формулы значительным образом упрощаются (sin(90°)=1, cos(90°)=0) и состоят, как правило, из двух множителей. Но более рационально производить решение по правилам Модюи-Непера, почти полностью исключающим промежуточные преобразования, а значит и ускоряющим решение (

Пример 3.2).

Правила Модюи-Непера формулируются следующим образом:

1) В прямоугольном сферическом треугольнике косинус любого среднего элемента равен произведению котангенсов крайних смежных с ним элементов.

2) Косинус отдельно лежащего элемента сферического треугольника равен произведению синусов двух не смежных с ним рядом лежащих элементов.

В обоих правилах принято, что катеты лежат рядом друг с другом и вместо катетов надо брать их дополнения до 90°.

Формул такого вида 10. Все они однотипны, поэтому для примера приведём четыре характерных:

( 3.8)

При А=90°

cos a = ctg B ctg C

cos B = ctg a ctg (90° – c)

( 3.9)

cos (90° – c) = sin C sin a

cos a = sin (90° – b) sin (90° – c)

Следовательно, в задаче на прямоугольный треугольник, надо задать два элемента и указать, какой угол равен 90°.

Пример 3.2

1) Выполняем схематический чертёж и помечаем данные и искомые элементы.

2) Подбираем необходимые формулы.

(по основным формулам сферической тригонометрии)

A, B – формула котангенсов;

c – формула косинуса стороны;

1. ctg A sin C = ctg a sin b – cos b cos C

2. ctg B sin C = ctg b sin a – cos a cos C

3. cos c = cos a cos b + sin a sin b cos C

3) Преобразовываем формулы и производим анализ на знаки. После преобразований независимо от первоначальных формул результат одинаков.

ctg A = ctg a sin b

ctg B = ctg b sin a

cos c = cos a cos b

(по правилам Модюи-Непера)

cos (90 – a) = ctg B ctg (90 – b)

cos (90 – b) = ctg A ctg (90 – a)

cos c = sin (90 – b) sin (90 – a)

ctg A = ctg a sin b

ctg B = ctg b sin a

cos c = cos a cos b

Не забываем, что отношение, это разность логарифмов

lg sin A = 9.76234 lg sin B = 9.99528 lg sin С =10,00000

lg sin a = 9.75263 lg sin b = 9.98557 lg sin c = 9.99029

0,00971 0.00971 0.00971

Четвертные сферические треугольники, как и прямоугольные можно решать по основным формулам сферической тригонометрии. Т.к. одна из сторон равна 90°, формулы значительным образом упрощаются (sin(90°)=1, cos(90°)=0) и состоят, как правило, из двух множителей. Возможен и другой путь решения: свести четвертной треугольник к полярному прямоугольному и производить решение по правилам Модюи-Непера.

Сферические треугольники ABC и A₁B₁C₁ называются полярными, если их стороны и углы связаны следующими соотношениями:

т.е. сумма угла данного треугольника с противоположной стороной полярного ему треугольника равна 180°.

Пример 3.3

Дано: a =31°15.2′, C = 120°15.4′

1) Выполняем схематический чертёж и помечаем данные и искомые элементы.

2) Подбираем необходимые формулы. (по основным формулам сферической тригонометрии)

A – теорема синусов

B – формула котангенсов;

c – формула косинуса стороны;

1.

2. ctg B sin C = ctg b sin a – cos a cos C

3. cos c = cos a cos b + sin a sin b cos C

3) Преобразовываем формулы, отделяем неизвестные, а так же производим анализ формулы на знаки.

1. sin A = sin a sin C

2. tg B = — cos a tg C

3. tg b = — ctg a sec C

а 90° sin C (+), sec C и tg C ( – )

Так как во всех формулах результат положителен, все искомые величины находятся в первой четверти.

4) Составляем схему вычислений и производим вычисления с использованием таблиц 5-а МТ-75(63) Таблица 3.6. Подробности использования таблиц приведены в пояснениях к таблицам. Что бы не менять наименования функций для аргументов больших 90° при входе в таблицу берём их дополнения до 180°.

lg	lg	lg
a=31°15.2′ C=120°15.4′	sin sin	9.71502 9.93640	cos tg	9.93191 0.23408	ctg sec	0.21687 0.29768
sin A	9.65142	tg B	0.16599	tg b	0.51455
A	26°37.5′	B	55°41.5′	b	72°59,8′
A=26°37.5′	B=55°41.5′	b=72°59,8′

5) Производим контроль вычислений по теореме синусов. Проверку можно производить как на калькуляторе, так и при помощи таблиц логарифмов.

lg sin a = 9.71502 lg sin b = 9.98059 lg sin с =10.00000

lg sin A = 9.65142 lg sin B = 9.91699 lg sin C = 9.93640

Треугольник Рёло// Материал из Википедии — свободной энциклопедии

— Режим доступа. — URL: http://ru. wikipedia. org/wiki/

3. Бронштейн, И. Н., Семендяев, К. А., Справочник по математике для инженеров и учащихся вузов.// – М.:Просвещение,1992.

4. Коксетер, С. М., Грейтцер, С. Л., Новые встречи с геометрией. //– М., Наука, 1978.-223с.

5. Конфорович, А. Г., Некоторые математические задачи//. – Киев, Родная школа, 1981.-189с.

6. Числа и фигуры — М., Физматгиз, 19с.

7. , Болтянский постоянной ширины // Выпуклые фигуры. — М.—Л.: ГТТИ, 1951. — С. 90—105. — 343 с.

Сайты в Интернете:

1. http://ru. wikipedia. org/wiki/%D0%A2%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA_%D0%A0%D1%91%D0%BB%D0%BE

2. http://www. *****/article/5480-kolesa-s-uglami/

3. http://www. *****/ru/etudes/mazda/

1. http://www. *****/images/upload/article/bike_1__preview2.jpg

2. http://www. *****/images/upload/article/bike_2__preview2.jpg

3. http://upload. wikimedia. org/wikipedia/commons/thumb/9/9b/Leonardo_da_Vinci%E2%80%99s_Mappamundi. jpg/220px-Leonardo_da_Vinci%E2%80%99s_Mappamundi. jpg

4. http://upload. wikimedia. org/wikipedia/commons/thumb/b/b2/Reuleaux_triangle%2C_incircle_and_circumcircle. svg/250px-Reuleaux_triangle%2C_incircle_and_circumcircle. svg. png

5. http://upload. wikimedia. org/wikipedia/commons/2/22/Rotation_of_Reuleaux_triangle. gif

6. http://upload. wikimedia. org/wikipedia/commons/thumb/2/2a/Luch2_greifer. gif/220px-Luch2_greifer. gif

7. http://upload. wikimedia. org/wikipedia/commons/thumb/b/bc/Manhole_cover_for_reclaimed_water_SFWD. JPG/220px-Manhole_cover_for_reclaimed_water_SFWD. JPG

8. http://upload. wikimedia. org/wikipedia/commons/thumb/d/d0/Reuleaux_triangles_on_a_window_of_Onze-Lieve-Vrouwekerk%2C_Bruges_2.jpg/450px-Reuleaux_triangles_on_a_window_of_Onze-Lieve-Vrouwekerk%2C_Bruges_2.jpg

9. http://upload. wikimedia. org/wikipedia/commons/thumb/2/21/Reuleaux_triangle_shaped_window_of_Sint-Salvatorskathedraal%2C_Bruges. jpg/125px-Reuleaux_triangle_shaped_window_of_Sint-Salvatorskathedraal%2C_Bruges. jpg

10. http://upload. wikimedia. org/wikipedia/commons/thumb/3/35/Reuleaux_triangles_on_a_window_of_Saint_Michael_church%2C_Luxembourg. jpg/800px-Reuleaux_triangles_on_a_window_of_Saint_Michael_church%2C_Luxembourg. jpg

11. http://upload. wikimedia. org/wikipedia/commons/thumb/9/9c/K%C3%B6lnTriangle_%28Flight_over_Cologne%29.jpg/125px-K%C3%B6lnTriangle_%28Flight_over_Cologne%29.jpg

12. http://upload. wikimedia. org/wikipedia/commons/thumb/e/eb/Reuleaux_triangles_on_a_window_of_Sint-Baafskathedraal%2C_Ghent_2.jpg/125px-Reuleaux_triangles_on_a_window_of_Sint-Baafskathedraal%2C_Ghent_2.jpg

13. http://upload. wikimedia. org/wikipedia/commons/thumb/4/4a/Reuleaux_triangle_shaped_window_of_Onze-Lieve-Vrouwekerk%2C_Bruges. jpg/125px-Reuleaux_triangle_shaped_window_of_Onze-Lieve-Vrouwekerk%2C_Bruges. jpg

Использование треугольника Рело в архитектуре

Окно церкви Богоматери в Брюгге

Окно собора Святого Сальватора в Брюгге

Окно собора Парижской Богоматери

Окно церкви Святого Михаила в Люксембурге

Окно церкви Богоматери в Брюгге

Окно собора Святых Михаила и Гудулы в Брюсселе

Сферические треугольники решение и формулы (Таблица)

Сферические треугольники.

На поверхности шара кратчайшее расстояние между двумя точками измеряется вдоль окружности большого круга, т. е. окружности, плоскость которой проходит через центр шара. Вершины сферического треугольника являются точками пересечения трех лучей, выходящих из центра шара, и сферической поверхности. Сторонами а, b, с сферического треугольника называют те углы между лучами, которые меньше 180°. Каждой стороне треугольникасоответствует дуга большого круга на поверхности шара (рис. 1). Углы A, В, С сферического треугольника, противолежащие сторонам а, b, с соответственно, представляют собой, по определению, меньшие, чем 180°, углы между дугами больших кругов, соответствующими сторонам треугольника, или углы между плоскостями, определяемыми данными лу­чами.

Свойства сферических треу­гольников.

Каждая сторона и угол сфери­ческого треугольника по определению мень­ше 180°. Геометрия на поверхности шара являет­ся неевклидовой; в каждом сферическом треугольнике сумма сторон заключена между 0 и 360°, сумма углов заключена между 180° и 540°. В каждом сферическом треуголь­нике против большей стороны лежит больший угол. Сумма любых двух сторон больше третьей стороны, сумма любых двух углов меньше, чем 180° плюс третий угол.

Сферический треугольник единственным образом определяется (с точностью до преобразования симметрии):

• тремя сторонами,
• тремя углами,
• двумя сторонами и заключенным между ними углом,
• стороной и двумя прилежащими к ней углами.

[править] Генерация сетки в сферическом треугольнике

Процедуру создания на некоторой поверхности сетки треугольников обычно называют триангуляцией. В качестве базы для создания сетки используем некоторый сферический треугольник, заданный координатами своих вершин.

Метод бисекции

Назовём бисекцией операцию деления исходного треугольника на четыре треугольника нового поколения. Собственно термин «бисекция» относится к делению сторон пополам. В середины рёбер вставляются новые вершины (белые точки на рисунках), которые соединяются новыми рёбрами (пунктирные линии), образующими новые треугольники. Следующее поколение получается очередной бисекцией.

В терминах геометрии на сфере задача вставки точек в стороны треугольников решается последовательным решением обратной и прямой геодезических задач. Однако в данном случае гораздо проще использовать векторную алгебру. Пусть концы стороны заданы векторами a и b; тогда средняя точка f вычисляется как их нормированная сумма:

Сферический треугольник

Сферический треугольник ABC расположен на поверхности сферы как показано на рисунках.

Стороны a, b, c (являющиеся дугами больших кругов) измеряются величинами опирающихся на них центральных углов. A, B, C есть углами, противоположными сторонам a, b, c соответственно.

Площадь сферического треугольника $ABC = (A + B + C — \pi)R^2$ где R — радиус сферы.

Отношение между сторонами и углами сферического треугольника

Правило косинусов cos a = cos b ⋅ cos c + sin b ⋅ sin c ⋅ cos A cos A = — cos B ⋅ cos C + sin B ⋅ sin C ⋅ cos a с подобными результатами при использовании других сторон и углов.

с подобными результатами при использовании других сторон и углов.

Подобные утверждения справедливы и для других углов и сторон.

где $S = \frac$. Подобные утверждения справедливы и для других углов и сторон.

Правила Непера для прямоугольного сферического треугольника

За исключением прямоугольного угла C, есть пять частей сферического треугольника ABC, которые приведены на рис. 5-19 и обозначены как a, b, A, c, B.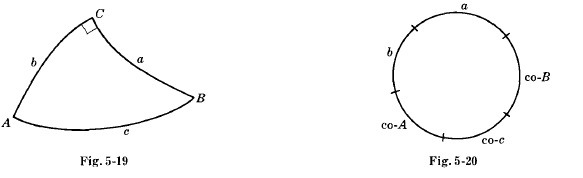

Предположим, что эти части расположены по кругу, как на рис. 5-20, где мы допишем префикс co (означающий дополнение) к гипотенузе c и углам A и B.

Любая из этих частей круга называется средняя часть, две другие соседние части называются смежные части и две другие оставшиеся части называются противоположные части.

Синус любой средней части равен произведению тангенсов смежных частей.

Синус любой средней части равен произведению косинусов противоположных частей.

Пример: Так как co-A = 90° — A, co-B = 90° — B, мы имеем sin a = tg b ⋅ tg(co-B) или sin a = tg b ⋅ ctg B sin(co-A) = cos a ⋅ cos(co-B) или cos A = cos a ⋅ sin B.

[править] Сферические многогранники

Сферический многогранник — разбиение сферы дугами больших окружностей на замкнутые области, называемые сферическими многоугольниками. Способы разбиения сферы ничем не ограничены. Однако регулярные построения обычно основаны на пространственной симметрии тетраэдра, октаэдра или икосаэдра.

Нас интересуют способы разбиения сферы на равносторонние или близкие к равносторонним треугольники. В центре такого треугольника построенная на его основе сетка будет близка к регулярной. Наибольшие искажения формы сетки будут вблизи углов базового треугольника. Несложный анализ показывает, что с позиции сохранения формы выгоднее всего опираться на симметрию икосаэдра. Подходящие многогранники — правильные и полуправильные, образованные треугольниками либо пяти- и шестиугольниками, которые разбиваются на почти равносторонние треугольники. Рассмотрим лишь несколько многогранников, удовлетворяющих этим требованиям.

Треугольник Рёло в искусстве, архитектуре и литературе

Форма треугольника Рёло, его свойство симметричности, используется и в архитектурных целях. Конструкция из двух его дуг образует характерную для готического стиля стрельчатую арку, однако целиком он встречается в готических сооружениях довольно редко. Окна в форме треугольника Рёло использовали еще в VIII векев церкви Богоматери в Брюгге, а также в шотландской церкви в Аделаиде. Как элемент орнамента он встречается на оконных решётках цистерцианского аббатства в швейцарской коммуне Отрив (приложение 1)

Треугольник Рёло используют и в архитектуре, не принадлежащей к готическому стилю. Например, построенная в 2006 году в Кёльне 103-метровая башня под названием «Кёльнский треугольник» в сечении представляет собой именно эту фигуру.

В научно-фантастическом рассказе Пола Андерсона «Треугольное колесо» экипаж землян совершил аварийную посадку на планете, население которой не использовало колёса, так как всё круглое находилось под религиозным запретом. В сотнях километров от места посадки предыдущая земная экспедиция оставила склад с запасными частями, но перенести оттуда необходимый для корабля двухтонный атомный генератор без каких-либо механизмов было невозможно. В итоге землянам удалось соблюсти табу и перевезти генератор, используя катки с сечением в виде треугольника Рёло.

Изобретение велосипеда с треугольными колесами

Колесо, изобретенное несколько тысяч лет назад, произвело переворот в жизни человека. Постоянство ширины явилось для колеса определяющим свойством, следствием которого явилось техническое завоевание мира.

Изобретением колес велосипеда занимается китайский рационализатор Гуань Байхуа (Guan Baihua), 50-летний офицер из города Циндао. Больше того, он изобретает заново самую консервативную деталь велосипеда – колеса. Вместо понятных всем круглых он предложил кататься на колесах пяти — и треугольной формы (спереди и сзади, соответственно). Для китайцев велосипед – главный вид транспорта, популярностью затмевающий автомобили. Но велосипед с угловатыми колесами средством передвижения не станет. По словам изобретателя, поездка на нем требует больше усилий, чем на обычном велосипеде, и скорее всего, он найдет свою нишу в качестве экзотической игрушки и более эффективного тренажера. Впрочем, все, кто пробовал прокатиться на нем, удивляются вовсе не трудности кручения педалей, а неожиданной плавности хода. Действительно, казалось бы, угловатые колеса неизбежно должны создавать при качении существенную тряску – но ее Гуаню Байхуа удалось снизить благодаря прекрасному знанию геометрии и настоящей китайской хитрости. .

Таким же образом можно устроить подвеску некруглого колеса и взяв четыре таких подвески, можно соорудить повозку. При этом она будет ехать совершенно без покачиваний! Чтоьы убедиться, что тряски нет, можно поставить, как учат автомобилистские традиции, на тележку стакан с водой.

Рисунок 11 Повозка с «треугольными» колесами.

Мы попробовали соорудить такую повозку и опытным путем проверить гипотезу об отсутствии качки.

Рисунок 12 «Треугольные» колеса.

Рисунок 13 Варианты повозки с «треугольными» колесами. Результаты эксперимента подтвердили нашу гипотезу.