Комплексные числа

Комплексные числа — определение и основные понятия

Обычные числа представляют собой множество действительных чисел, для обозначения которых используют букву R. Каждое число из множества можно отметить на числовой прямой.

К действительным числам носят:

• целые числа;
• дроби;
• иррациональные числа.

Каждая точка на числовой прямой характеризуется некоторым действительным числом. Комплексное число является двумерным числом и записано в виде:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

z = a + bi

Где а и b являются действительными числами, i представляет собой так называемую мнимую единицу.

Уравнение можно мысленно поделить на несколько частей:

• a — действительная часть (Re z) комплексного числа z;
• b — мнимая часть (Im z) комплексного числа z.

Следует отметить, что a + bi является единым числом, а не сложением. Места действительной и мнимой частей в уравнении можно менять:

z = bi + a

Мнимую единицу допускается переставлять:

z = a + ib

При таких операциях смысл выражения остается прежним. Однако стандартная запись комплексного числа имеет такой вид:

z = a + bi

Определение

Комплексным числом называют выражение a + bi, в котором а и b являются действительными числами, i представляет собой мнимую единицу, символ, квадрат которого равен -1, то есть i2=-1. Число а представляет собой действительную часть, b — мнимую часть комплексного числа z = a + bi. Если b = 0, то вместо a + 0i записывают a. Действительные числа являются частным случаем комплексных чисел.

Данное утверждение можно привести в виде геометрической интерпретации. Тогда комплексные числа изображают на комплексной плоскости.

С помощью R обозначаю множество действительных чисел. В случае, когда требуется обозначить множество комплексных чисел, принято использовать букву С. Наличие буквы С на чертеже говорит о том, что на нем представлена комплексная плоскость. Данная плоскость включает две оси:

Re z — является действительной осью;

Im z — представляет собой мнимую ось.

Правила оформления такого графика практически не отличаются от требований к чертежам для декартовой системы координат. По осям задают масштаб и отмечают:

• ноль;
• единицу для действительной оси;
• мнимую единицу i для мнимо оси.

С помощью комплексной плоскости можно построить заданные комплексные числа:

\(z_{1}=0\)

\(z_{2}=-3\)

\(z_{3}=2\)

\(z_{4}=i\)

\(z_{5}=-\sqrt{3}i\)

\(z_{6}=4i\)

\(z_{7}=2+3i\)

\(z_{8}=-4+i\)

\(z_{9}=-3-3i\)

\(z_{5}=-\sqrt{2}-i\)

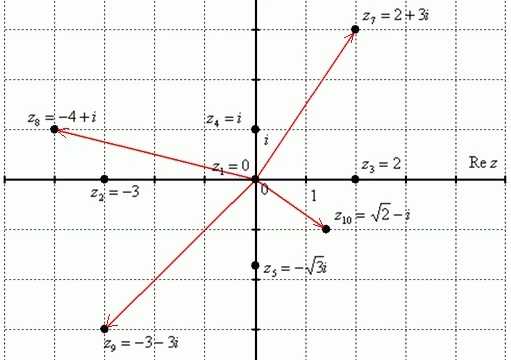
Можно рассмотреть следующие комплексные числа:

\(z_{1}=0\)

\(z_{2}=-3\)

\(z_{3}=2\)

Действительные числа являются частным случаем комплексных чисел. Действительная ось Re z обозначает в точности множество действительных чисел R, то есть на данной оси расположены все числа с обычными свойствами. Можно сформулировать справедливое утверждение: множество действительных чисел R представляет собой подмножество множества комплексных чисел С.

Данные числа являются комплексными числами, мнимая часть которых нулевая:

\(z_{1}=0\)

\(z_{2}=-3\)

\(z_{3}=2\)

Мнимые числа с нулевой действительностью, которые расположены на мнимой оси Im z:

\(z_{4}=i\)

\(z_{5}=-\sqrt{3}i\)

\(z_{6}=4i\)

Есть ряд чисел с ненулевыми действительной и мнимой частью:

\(z_{7}=2+3i\)

\(z_{8}=-4+i\)

\(z_{9}=-3-3i\)

\(z_{5}=-\sqrt{2}-i\)

Для их обозначения используют точки на комплексной плоскости. К таким точкам проводят радиус-векторы из начала координат. Радиус-векторы не принято чертить к числам, которые расположены на осях и сливаются с ними.

Возведение в степень и извлечение корня из комплексного числа

Возведение в натуральную степень равносильно умножению числа самого на себя $n$ раз: $$ z^n=z\cdot z\cdot\ldots\cdot z. $$

Формула для степени комплексного числа в показательной и тригонометрической формах: $$ z^n=(x+\mathbf i y)^n=\big(r(\cos\varphi+\mathbf i \sin\varphi)\big)^n=
\left(re^{\mathbf i \varphi}\right)^n=
$$ $$ =r^ne^{\mathbf i n\varphi}=r^n(\cos n\varphi+\mathbf i \sin n\varphi). $$ Отсюда получим формулу Муавра (1667-1754):
\begin{equation}\label{eq g1 p5 1}
(\cos\varphi+\mathbf i \sin\varphi)^n=\cos n\varphi+\mathbf i \sin n\varphi.
\end{equation}

В качестве $\varphi$ можно брать как $\mbox{Arg }z$, так и
$\arg z$, так как $$ e^{\mathbf i\mbox{Arg }z}=e^{\mathbf i \arg z+2\pi k\mathbf i}=e^{\mathbf i \arg z}e^{2\pi k\mathbf i}=e^{\mathbf i \arg z}, $$ ибо по формуле Эйлера $e^{2\pi k \mathbf i}=1$.

П

Пример. С помощью формулы Муавра выразить
$\cos3\varphi$ и $\sin3\varphi$ через $\cos\varphi$ и $\sin\varphi$.

О т в е т:
$\cos3\varphi=4\cos^3\varphi-3\cos\varphi, \,\, \sin3\varphi=-4\sin^3\varphi+3\sin\varphi$.

Число $w$ называется корнем натуральной степени из числа
$z\ne0$, если
\begin{equation}\label{g1 p5 2}
w^n=z.
\end{equation}
Обозначается $w=\sqrt{z}$, для $n=2$ имеем $w=\sqrt{z}$.

Вывод формулы $\sqrtz$. Пусть $$
\begin{array}{l}
z=r(\cos\varphi+\mathbf i \sin\varphi),\\
w=\rho(\cos\theta+i\sin\theta).
\end{array}
$$
Тогда
$$
\begin{array}{c}
w^n=\rho^n(\cos n\theta+\mathbf i \sin n\theta)= \\
=r(\cos\varphi+\mathbf i \sin\varphi).
\end{array}
$$
Приравнивая вещественные составляющие левой и правой частей, находим
$\rho^n=r$, а затем и $n\theta = \varphi+2\pi m=\arg z+2\pi k$. Получаем
$$
\begin{array}{l}
\rho=\sqrt{r}, \\
\theta=\dfrac1n\mbox{Arg }z=\dfrac1n\big(\arg z+2\pi k\big).
\end{array}
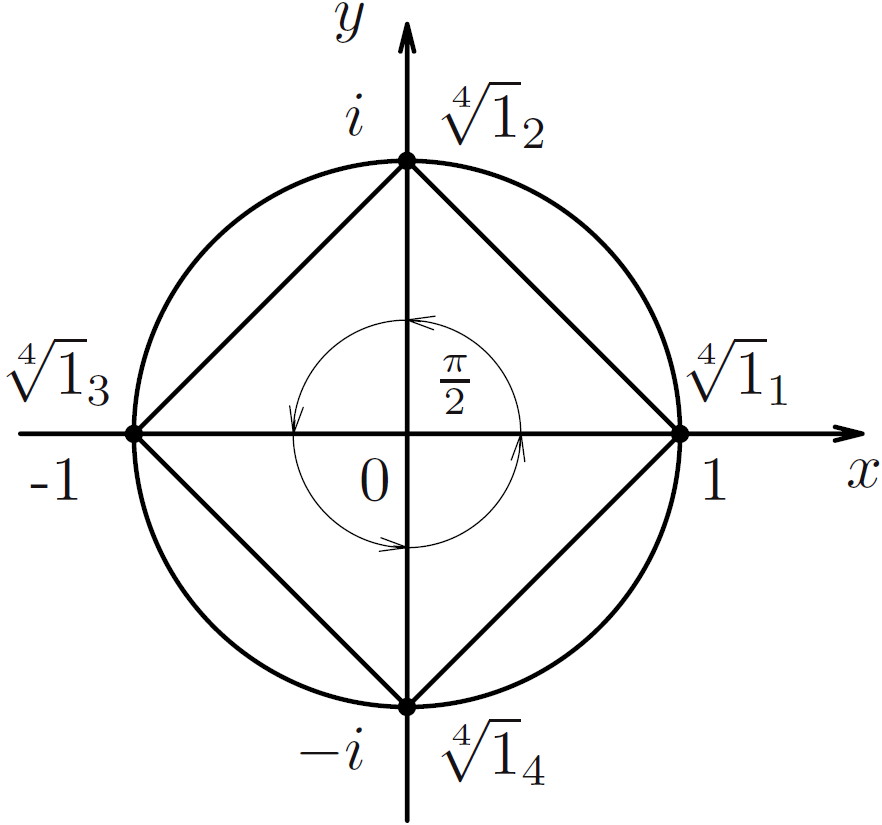
$$
Корень $n$-й степени из комплексного числа имеет $n$ различных
значений при $k=0,1,\ldots,n-1$:
$$
w_k=\sqrt{r(\cos\varphi+\mathbf i \sin\varphi)}=\!\sqrt{r}\left(\cos
\frac{\arg z+2\pi k}n+\mathbf i \sin\frac{\arg z+2\pi k}n\right).
$$

Геометрически эти $n$ значений корня изображаются вершинами правильного $n$-угольника с полярными координатами $\Big(\sqrtr,$ $\dfrac1n(\arg
z+2\pi k)\Big)$.

П

Пример. Найдем по формулам $\sqrt1=\{1,\mathbf i ,-1,-\mathbf i \}$. Эти точки
находятся в вершинах квадрата.

Расширенная комплексная плоскость. Сфера Римана

Из геометрии известно, что любой упорядоченной паре вещественных чисел соответствует точка $z$ на плоскости комплексного переменного. Определим
на комплексной плоскости бесконечно удаленную точку. Так условно будем называть «мысленную точку» $(x,y)$, координаты которой (обе сразу
или одна из них) — величины неограниченные, т.е. комплексные числа имеют формальный вид $z=x+i\infty$, $z=\infty+iy$ либо $z=\infty+i\infty$.
Тогда пишут $z=\infty$ (несобственное комплексное число), считая ее единственной бесконечно удаленной точкой.

Для несобственного комплексного числа понятия вещественной и мнимой части, а также понятие аргумента не вводятся; точнее говоря, объявляются
лишенными смысла (напомним, что понятие аргумента не имеет смысла и для числа 0). Что касается модуля числа $z=\infty$, то для него используется
символ $|\infty|=+\infty$.

Договорились, что имеют смысл следующие операции, в которых участвуют $z=\infty$ и собственное комплексное число $a$: $$
\frac{a}\infty=0,\quad\frac\infty{a}=\infty,\quad\frac{a}0=\infty.
$$ Такие операции, как $$
\infty\pm\infty,\quad 0\cdot\infty,\quad \dfrac00,\quad
\dfrac\infty\infty
$$ объявляются лишенными смысла.

Совокупность точек комплексной плоскости и бесконечно удаленной точки называется расширенной плоскостью комплексного переменного.

Наглядное представление о расширенной комплексной плоскости дает следующая интерпретация Римана (1826-1866).

Чтобы получить геометрическое изображение числа $\infty$, прибегают к представлению комплексных чисел точками сферы. Построим сферу (называемую сферой Римана) радиуса $r$, касающуюся плоскости $z$ в точке $z=0$ и отметим точку $N$ сферы, диаметрально противоположную началу
координат $O$.

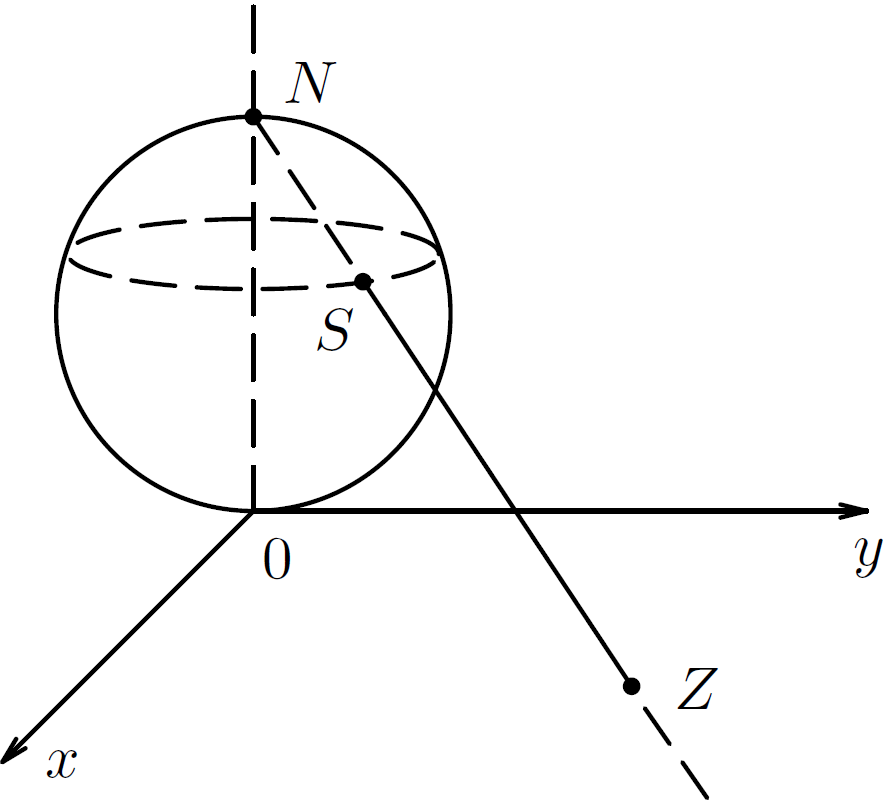
Из точки $N(0,0,2r)$ сферы проведем проведем луч в любую точку $Z(x,y,0)$ плоскости $(x,y)$ и отметим точку $S$ пересечения данного луча и
сферы. Эта точка $S(\xi,\eta,\zeta)$ является новым геометрическим представлением комплексного числа $z$. В результате таких
построений лучей между точками плоскости $(x,y)$ и точками сферы устанавливается взаимно однозначное соответствие, называемое стереографической
проекцией, имеющей применение в картографии.

Точкам меридиана $NSO$ на сфере соответствуют точки луча $OZ$ на плоскости $(x,y)$, различным параллелям — круги на плоскости $(x,y)$.
Исключение составляет точка $N$. Северному полюсу $N$ сферы не соответствует пока никакое комплексное число. Однако точкам сферы, достаточно
близким к $N$, соответствуют точки $z$ плоскости, сколь угодно далеко отстоящие от начала координат, т.е. точка $z$ сколь угодно большого
модуля. Будем считать, что точке $N$ соответствует единственная точка $z=\infty$.

Покажем, что точка $z=\infty+\mathbf i \infty$ (или $z=x+\mathbf i \infty$, или $z=\infty+\mathbf i y$) будет при таком преобразовании переходить в точку $N(0,0,2r)$ и
наоборот. Координаты точек на такой сфере $(\xi,\eta,\zeta)$ связаны формулой
\begin{equation}\label{eq g1 p7 1}
\xi^2+\eta^2+(\zeta-r)^2=r^2\quad\hbox{или}\quad \xi^2+\eta^2=\zeta
(2r-\zeta).
\end{equation}

Из коллинеарности $NZ$ и $NS$ можно получить представление луча $NSZ$
$$
\frac{\xi-0}{x-0}=\frac{\eta-0}{y-0}=\frac{\zeta-2r}{0-2r}.
$$
Отсюда можно получить координаты точек плоскости через координаты точек сферы:
\begin{equation}\label{eq g1 p7 2}
x=\frac{2r\xi}{2r-\zeta},\quad y=\frac{2r\eta}{2r-\zeta}.
\end{equation}

Составим
$$ x^2+y^2=\frac{4r^2(\xi^2+\eta^2)}{(2r-\zeta)^2}, $$
$$ x^2+y^2 = \frac{4r^2\zeta}{2r-\zeta}. $$
Тогда
можно выразить координату
$$
\zeta=\frac{2r(x^2+y^2)}{x^2+y^2+4r^2},
$$
и другие координаты
$$
\xi=\frac{4r^2x}{x^2+y^2+4r^2},\quad\eta=\frac{4r^2y}{x^2+y^2+4r^2}.
$$

Устремим $x\to\infty$, $y\to\infty$ (по отдельности или вместе), тогда $\xi\to0$, $\eta\to0$, $\zeta\to2r$, а это и есть точка $N$.

Некоторые сведения о комплексных числах подробнее изложены в курсе Высшей алгебры А.Ю. Утешева ( здесь).

Краткая вводная

Когда-то нам хватало натуральных чисел:

\

Всё было прекрасно: «У тебя 5 бананов, у меня ещё 3 — итого у нас 5 + 3 = 8 бананов». Сумма двух натуральных чисел всегда даёт новое натуральное число (говорят, что операция сложения замкнута на множестве натуральных чисел).

Но вот на сцену выходит вычитание — и натуральных чисел стало недостаточно. Например разность 3 − 5 = −2 уже не будет натуральным. Так появились целые числа (натуральные, им противоположные и ноль):

\

Дальше к делу подключились операции умножения и деления. Да, произведение двух целых чисел всё ещё целое, но вот деление приводит к образованию дробей. Например, 1 : 2 или 5 : 4 уже нельзя записать целым числом. Так появилось множество рациональных чисел или множество дробей:

\

Это был настоящий триумф для древней математики, и в тот момент казалось, что ничего больше уже изобрести нельзя. Да и зачем?

Проблема пришла откуда не ждали. В какой-то момент классическое умножение «разрослось» до возведения в степень:

\

Тут-то и выяснилось, что возведение рационального числа в натуральную степень всё ещё будет рациональным числом. Но вот обратная операция — извлечение корня — выносит нас за пределы рациональных чисел:

\

Так появилось множество действительных чисел — множество бесконечных десятичных дробей, которые могут быть периодическими (и тогда это обычное рациональное число) и непериодическими (такие числа называют иррациональными, и их неизмеримо больше).

\

Казалось бы: ну вот теперь точно всё! Что ещё нужно для счастья? Проблема в том, что на множестве действительных чисел нельзя извлечь даже самый простой квадратный корень из отрицательного числа:

\

Однако законы физики (особенно электродинамика и вообще всё, где есть слово «динамика») как бы намекали, что множество содержательных процессов протекает там, где привычные корни не извлекаются. А значит, следует расширить множество действительных чисел так, чтобы такие корни всё же извлекать.

И тут открылись врата в Ад…

Изображение комплексных чисел радиус-векторами координатной плоскости

      Рассмотрим плоскость с заданной на ней   Oxy   и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.

      Назовем рассматриваемую плоскость комплексной плоскостью, и будем представлять комплексное число   z = x + i y   радиус–вектором с координатами   (x , y).

      Назовем ось абсцисс Ox вещественной осью, а ось ординат Oy – мнимой осью.

      При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.

Понятие комплексного числа

В качестве обозначения множества, которое составляют комплексные числа, в алгебре используют букву «С».

Любое комплексное число z = a+bi включает в состав пару компонентов, которые называются и обозначаются так:

• a является вещественной составляющей числа z;
• b является мнимым компонентом числа z.

В том случае, когда b бывает равно нулю, z считают вещественным числом. Заменой выражения a+0i является просто а. К примеру, чтобы обозначить комплексный ноль 0+0i, записывают кратко 0.

Комплексное число z=a+bi является противоположным числу -z=-a-bi. Это правило выполняется, к примеру, если дано число 1-2i, то противоположным ему станет число -1+2i.

Комплексные числа отличаются от вещественных еще и тем, что их нельзя сравнить между собой на «больше» или «меньше». С другой стороны, допустимо сравнение комплексных чисел на равенство или неравенство.

Если мнимая и вещественная части, из которых состоит одно комплексное число, равны соответствующим частям другого комплексного числа, то такие комплексные числа равны. Например, a+bi=c+di. Таким образом, a=c и b=d.

Комплексная единица

Начнём с ключевого определения.

Очевидно, комплексная единица не является привычным нам действительным числом: $i\notin \mathbb{R}$. Просто потому что квадрат действительного числа не может быть отрицательным.

Однако в остальном это такое же число, как и все остальные. Комплексные единицы можно складывать, умножать, их можно комбинировать с «нормальными» числами:

\

В последнем примере мы сгруппировали слагаемые и провели подобные — совсем как с многочленами. Нельзя напрямую сложить действительное число и комплексную единицу, поскольку сущность числа $i$ нам не ясна. Но привести подобные — всегда пожалуйста.

И это первое замечательное свойство комплексной единицы. По сути, работать с ней — всё равно что работать с многочленом. Просто вместо переменной $x$ теперь будет $i$. Ну и помним, что ${{i}^{2}}=-1$, что ещё больше упрощает жизнь:

\

Обратите внимание: запись $1+i$ является окончательной, её нельзя упростить. Точно так же нельзя упростить многочлен $kx+b$, например

И тут мы плавно переходим к следующему пункту.

Умножение и деление комплексных чисел, записанных в тригонометрической или показательной формах

Пусть даны два комплексных числа, записанных в тригонометрической форме
$$
\begin{array}{l}
z_1=r_1(\cos\varphi_1+\mathbf i \sin\varphi_1), \\
z_2=r_2(\cos\varphi_2+\mathbf i \sin\varphi_2).
\end{array}
$$ Выведем формулу для произведения: $$ z_1z_2=r_1r_2\big(\cos\varphi_1\cos\varphi_2-\sin\varphi_1\sin
\varphi_2+\mathbf i (\sin\varphi_1\cos\varphi_2+
$$ $$ +\cos\varphi_1\sin\varphi_2)\big) = r_1r_2\big(\cos(\varphi_1+
\varphi_2)+\mathbf i \sin(\varphi_1+\varphi_2)\big).
$$ Для деления получим следующую формулу $(z_2\ne0)$: $$
\frac{z_1}{z_2}=\frac{r_1(\cos\varphi_1+i\sin\varphi_1)}{r_2(\cos
\varphi_2+i\sin\varphi_2)}=\frac{r_1(\cos\varphi_1+i\sin\varphi_1)
(\cos\varphi_2-i\sin\varphi_2)}{r_2(\cos\varphi_2+i\sin\varphi_2) (\cos\varphi_2-i\sin\varphi_2)} = $$ $$
=\frac{r_1}{r_2}\big(\cos\varphi_1\cos\varphi_2+\sin\varphi_1
\sin\varphi_2+\mathbf i (\sin\varphi_1\cos\varphi_2-\cos\varphi_1
\sin\varphi_2)\big)=
$$ $$ =\frac{r_1}{r_2}\big(\cos(\varphi_1-\varphi_2)+ \mathbf i \sin(\varphi_1-\varphi_2)\big). $$

Умножение, деление удобнее производить в показательной форме. Пусть $z_1=r_1e^{\mathbf i \varphi_1}$, $z_2=r_2e^{\mathbf i\varphi_2}$, тогда произведение и
частное (считая $z_2\neq 0$): $$ z_1z_2=r_1r_2\,e^{\mathbf i (\varphi_1+\varphi_2)},\quad
\frac{z_1}{z_2}=\frac{r_1}{r_2}\,e^{\mathbf i (\varphi_1-\varphi_2)}.
$$

Комплекснозначные функции действительного переменного.

Если каждому значению \(t\in \) поставлено в соответствие комплексное число \(z=z(t)\), то говорят, что на отрезке \(\) задана комплекснозначная функция действительного переменного.

Пусть \(\operatorname{Re}z(t) = x(t),\ \operatorname{Im}z(t) = y(t)\), тогда \(z(t) = x(t)+iy(t)\). Функцию \(z(t)\) можно рассматривать как вектор-функцию \(z(t)=(x(t),y(t))\). Определения предела, непрерывности, производной для комплекснозначной функции аналогичны соответствующим определениям для вектор-функции.

Например, производная функции \(z(t) = x(t) + iy(t)\) определяется формулой
$$
z'(t) = x'(t) + iy'(t).\label{ref25}
$$
Следовательно, производная \(z'(t)\) существует, если существуют производные \(x'(t)\) и \(y'(t)\).

Применяя формулу \eqref{ref25} к функции \(e^{it}=\cos t+i\sin t\), получаем \((e^{it})’=-\sin t+i\cos t=i^2\sin t + i\cos t = i(\cos t + i\sin t)\), то есть
$$
(e^{it})’=i e^{it}.\label{ref26}
$$

Таким образом, формула для производной комплексной функции \(e^{it}\) имеет такой же вид, как и для функции \(e^{\alpha t}\), где \(\alpha\in\mathbb{R}\).

Определим теперь показательную функцию \(\displaystyle e^{(\alpha+i\beta)t}\), где \(\alpha,\beta\) — заданные действительные числа, \(t\) — действительное переменное. Функция \(f(t) = e^t\), где \(t\in\mathbb{R}\), удовлетворяет условию
$$
f(t_1)f(t_2) = f(t_1+t_2).\label{ref27}
$$

Аналогично функция \(e^{i\beta t}\), где \(\beta\in\mathbb{R}\), обладает свойством \eqref{ref27} в силу первого из равенств \eqref{ref18}.

Поэтому функцию    \(e^{(\alpha+i\beta)t}\) естественно определить так, чтобы для нее выполнялось условие \eqref{ref27}, то есть
$$
e^{(\alpha+i\beta)t}=e^{\alpha t}e^{i\beta t}.\nonumber
$$

Используя формулу \eqref{ref15}, отсюда находим
$$
e^{(\alpha+i\beta)t} = e^{\alpha t} (\cos \beta t+i\sin\beta t).\label{ref28}
$$
Применяя к функции \(e^{\lambda t}\), где \(\lambda=\alpha+i\beta\), правило дифференцирования \eqref{ref25}, легко показать, что
$$
(e^{\lambda t})=\lambda e^{\lambda t},\quad \lambda=\alpha+i\beta.\label{ref29}
$$

По аналогии с производной неопределенный интеграл от комплекснозначной функции \(z(t)=x(t)+iy(t)\) определяется формулой
$$
\int z(t) dt = \int x(t) dt + i\int y(t) dt.\nonumber
$$

Если комплексная функция \(\omega(t) = \xi(t) + i\eta (t)\) такова, что \(\omega'(t)=z(t)\), то
$$
\int z(t)=\int \omega'(t)dt=\int \xi'(t)dt+i\int \eta'(t)dt = \xi(t) + C_1 + i\eta(t)+iC_2.\nonumber
$$
Следовательно,
$$
\int z(t) dt = \omega(t) + C,\quad C = C_1+iC_2.\nonumber
$$
Применяя это утверждение к функции \(e^{(\alpha+i\beta)t}\) и используя формулу \eqref{ref29}, получаем
$$
\int e^{(\alpha+i\beta)t}=\displaystyle \frac{e^{(\alpha+i\beta)t}}{\alpha+i\beta}+C_1+iC_2.\label{ref30}
$$

Выделяя в равенстве \eqref{ref30} действительные и мнимые части, находим
$$
\int e^{\alpha t}\cos\beta t dt + i\int e^{\alpha t}\sin\beta t dt = \frac{\alpha-i\beta}{\alpha^2+\beta^2}e^{\alpha t}(\cos\beta t+i\sin\beta t)+C_1+C_2,\nonumber
$$
откуда получаем
$$
\int e^{\alpha t}\cos\beta t dt=\frac{e^{\alpha t}}{\alpha^2+\beta^2}(\alpha\cos\beta t+\beta\sin\beta t)+C_1,\label{ref31}
$$
$$
\int e^{\alpha t}\sin\beta t dt=\frac{e^{\alpha t}}{\alpha^2+\beta^2}(\alpha\sin\beta t-\beta\cos\beta t)+C_2,\label{ref32}
$$

Заметим, что формула \eqref{ref31} была получена с помощью в .

Геометрическая интерпретация комплексных чисел

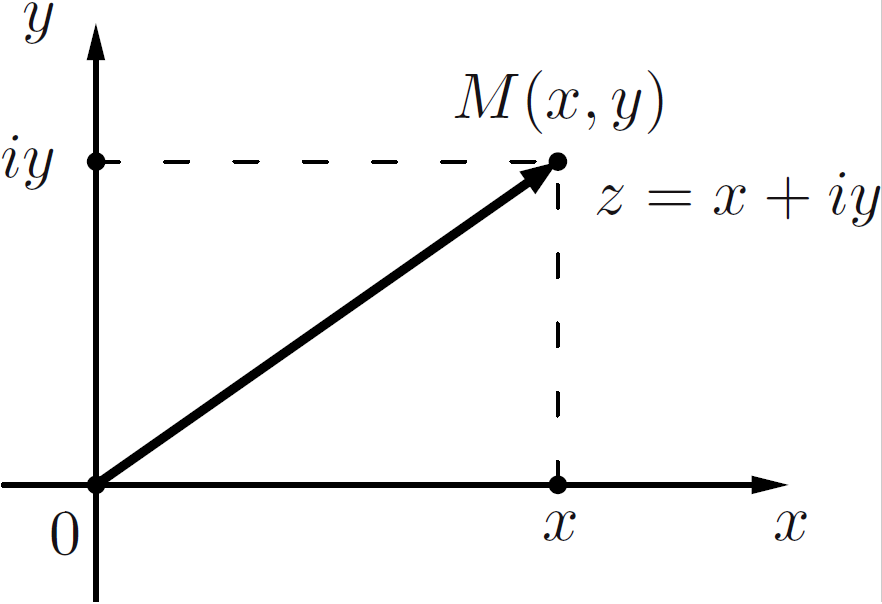
В 1799 году датчанин Каспар Вессель определил комплексное число как упорядоченную пару вещественных чисел $(x,y)$. Известно, что на декартовой
плоскости упорядоченной паре соответствует точка. Выберем на плоскости прямоугольную систему координат и установим взаимно однозначное
соответствие между комплексными числами и точками плоскости, при котором комплексному числу $z=x+\mathbf i y$ отвечает точка $M$ с координатами
$x,y$. Точку $M$ мы рассматриваем как изображение комплексного числа $z=x+\mathbf i y$.

При этом множество всех вещественных чисел изображается осью абсцисс, называемой поэтому вещественной осью, множество всех чисто мнимых
чисел лежит на оси ординат, называемой мнимой осью. Плоскость $XOY$, точки которой изображают комплексные числа, называется комплексной плоскостью (иногда гауссовой плоскостью) или просто плоскостью $z$. Термины «комплексное число $z$» и «точка $z$ на комплексной плоскости» употребляются как синонимы.

Комплексное число $z=x+\mathbf i y$ может также изображаться вектором с проекциями $x$ и $y$ на координатные оси, который, таким образом, равен
радиус-вектору точки $z$. Иногда термины «комплексное число» и «вектор» употребляют также как синонимы.

Именно поэтому, глядя на координатную плоскость,
естественно сделать вывод, что комплексные числа невозможно сравнивать, т.е. нельзя говорить, что какое-то комплексное число больше или меньше другого.

Комплексное число равное сумме или разности двух комплексных чисел $z_1\pm z_2$ соответствует вектору на комплексной плоскости, который получится при сложении/вычитании векторов, соответствующих числам $z_1$ и $z_2$. Для произведения $z_1\cdot z_2$ этой аналогии уже не будет.

Напомним, что в полярных координатах точка $M$ имеет координаты $(r,\varphi)$. В нашем случае полярные координаты имеют следующий смысл:

полярный радиус (или длина вектора) называется модулем комплексного числа $z=x+\mathbf i y$ и вычисляется по формуле

$$
r=|z|=\sqrt{x^2+y^2}=\sqrt{z\bar z},
$$

полярный угол $\varphi$ (угол между положительным направлением оси $OX$ и отрезком $OM$) называется аргументом комплексного числа $z$ и обозначается $\varphi=\mbox{Arg }z$.

Модуль и аргумент — две важнейшие характеристики комплексного числа.

Условия равенства двух комплексных чисел $z_1$ и $z_2$ — равенство их модулей: $|z_1|=|z_2|$ и аргументов: $\mbox{Arg }z_1=\mbox{Arg }z_2$.

Особый разговор об аргументе

Угол $\varphi=\mbox{Arg }z$ — аргумент комплексного числа $z=x+\mathbf i y$. Этот угол, изменяясь от положительного направления оси $OX$ против часовой
стрелки, увеличивается до $2\pi$, а далее его величины повторяются. Поэтому аргумент комплексного числа бесконечнозначен, так как все его
значения отличаются друг от друга на слагаемые, кратные $2\pi$.

Аргумент $\varphi$ определяется из формул
\begin{equation}
\left\{\begin{array}{l}
x=r\cos\varphi, \\
y=r\sin\varphi
\end{array}\right.
\end{equation}
с точностью до слагаемого $2\pi k$: $$
\mbox{Arg }z=\mbox{arg }z+2\pi k,\quad k=0,\pm1,\pm2,\ldots\ .
$$

Из множества значений аргумента особо выделяется главное значение $\mbox{arg }z$, удовлетворяющее неравенству $-\pi<\mbox{arg } z\le\pi$. При этом полезны
формулы
\begin{equation}
\arg z=\left\{\begin{array}{ll}
\mbox{arctg }\dfrac{y}{x},&x>0, \\
\mbox{arctg }\dfrac{y}{x}+\pi,&x<0,\ y\ge0, \\
\mbox{arctg }\dfrac{y}{x}-\pi,&x<0,\ y<0.\\
\end{array}\right.
\end{equation}

Для комплексного числа $z=0+\mathbf i 0$ понятие аргумента не
имеет смысла.

Условие сопряжения двух чисел $z$ и $\bar{z}$:
$$|z|=|\bar{z}|,\quad \arg z=-\arg \bar{z}.$$

Некоторые свойства модуля:
$$
\left| z_1 + z_2 \right| \le \left| z_1\right| + \left| z_2\right| \ ,
$$
$$
\left| z_1 + z_2 \right| \ge \big| | z_1 | — | z_2 | \big| \ ,
$$
$$
\left| z_1 — z_2 \right| \ge \big| | z_1 | — | z_2 | \big|.
$$