Медиана

Графический способ определения медианы

Графически медиана рассчитывается на базе кумуляты. Для её определения из точки на оси накопленных частот (или частостей), соответствующей 50%, строится прямая линия, которая должна быть параллельна оси абсцисс, до пересечения этой линии с кумулятой. Далее из точки пересечения построенной прямой линии с кумулятой строится перпендикуляр на ось абсцисс. Абсцисса точки пересечения и показывает величину медианы.

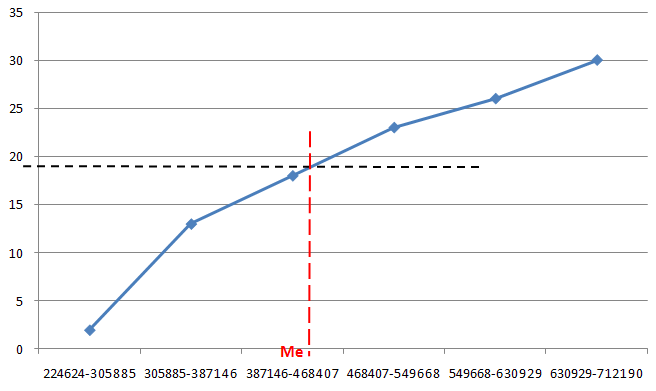Пример кумуляты распределения с графическим способом определения медианы

Больше примеров смотрите на странице Решение задач по статистике

Цена консультации по работе Пример расчета медианы — договорная.

Чтобы оформить заявку на получение файла с готовой работой или заказ на консультацию и помощь с работой по указанной теме по Вашим требованиям нажмите кнопку:

Формула медианы

Формула медианы в статистике для дискретных данных чем-то напоминает формулу моды. А именно тем, что формулы как таковой нет. Медианное значение выбирают из имеющихся данных и только, если это невозможно, проводят несложный расчет.

Первым делом данные ранжируют (сортируют по убыванию). Далее есть два варианта. Если количество значений нечетно, то медиана будет соответствовать центральному значению ряда, номер которого можно определить по формуле:

где

№_Me – номер значения, соответствующего медиане,

N – количество значений в совокупности данных.

Тогда медиана обозначается, как

Это первый вариант, когда в данных есть одно центральное значение. Второй вариант наступает тогда, когда количество данных четно, то есть вместо одного есть два центральных значения. Выход прост: берется средняя арифметическая из двух центральных значений:

В интервальных данных выбрать конкретное значение не представляется возможным. Медиану рассчитывают по определенному правилу. 

Для начала (после ранжирования данных) находят медианный интервал. Это такой интервал, через который проходит искомое медианное значение. Определяется с помощью накопленной доли ранжированных интервалов. Где накопленная доля впервые перевалила через 50% всех значений, там и медианный интервал.

Не знаю, кто придумал формулу медианы, но исходили явно из того предположения, что распределение данных внутри медианного интервала равномерное (т.е. 30% ширины интервала – это 30% значений, 80% ширины – 80% значений и т.д.). Отсюда, зная количество значений от начала медианного интервала до 50% всех значений совокупности (разница между половиной количества всех значений и накопленной частотой предмедианного интервала), можно найти, какую долю они занимают во всем медианном интервале. Вот эта доля аккурат переносится на ширину медианного интервала, указывая на конкретное значение, именуемое впоследствии медианой.

Обратимся к наглядной схеме.

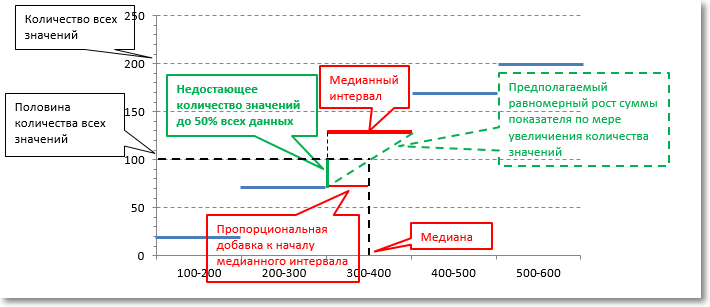
Немного громоздко получилось, но теперь, надеюсь, все наглядно и понятно. Чтобы при расчете каждый раз не рисовать такой график, можно воспользоваться готовой формулой. Формула медианы имеет следующий вид:

где x_Me — нижняя граница медианного интервала;

i_Me — ширина медианного интервала;

∑f/2 — количество всех значений, деленное на 2 (два);

S_(Me-1)— суммарное количество наблюдений, которое было накоплено до начала медианного интервала, т.е. накопленная частота предмедианного интервала;

f_Me — число наблюдений в медианном интервале.

Как нетрудно заметить, формула медианы состоит из двух слагаемых: 1 – значение начала медианного интервала и 2 – та самая часть, которая пропорциональна недостающей накопленной доли до 50%. 

Для примера рассчитаем медиану по следующим данным.

Требуется найти медианную цену, то есть ту цену, дешевле и дороже которой по половине количества товаров. Для начала произведем вспомогательные расчеты накопленной частоты, накопленной доли, общего количества товаров.

По последней колонке «Накопленная доля» определяем медианный интервал – 300-400 руб (накопленная доля впервые более 50%). Ширина интервала – 100 руб. Теперь остается подставить данные в приведенную выше формулу и рассчитать медиану.

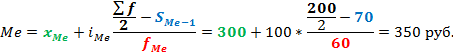
То есть у одной половины товаров цена ниже, чем 350 руб., у другой половины – выше. Все просто. Средняя арифметическая, рассчитанная по этим же данным, равна 355 руб. Отличие не значительное, но оно есть.

Расчет медианы в Excel

Медиану для числовых данных легко найти, используя функцию Excel, которая так и называется — МЕДИАНА. Другое дело интервальные данные. Соответствующей функции в Excel нет. Поэтому нужно задействовать приведенную выше формулу. Что поделаешь? Но это не очень трагично, так как расчет медианы по интервальным данным – редкий случай. Можно и на калькуляторе разок посчитать.

Напоследок предлагаю задачку. Имеется набор данных. 15, 5, 20, 5, 10. Каково среднее значение? Четыре варианта:

а) 11;

б) 5;

в) 10;

г) 5, 10, 11.

Мода, медиана и среднее значение выборки – это разный способ определить центральную тенденцию в выборке.

Ниже видеоролик о том, как рассчитать медиану в Excel.

Задача №2. Нахождение моды и медианы для дискретного ряда.

тарифный разряд, Xi	Число рабочих f	Частость, w	Накопленная частота, S
2	1	0,05	1
3	5	0,25	6
4	8	0,4	14
5	4	0,2	18
6	2	0,1	20
Итого:	2	1,0	20

Распределение рабочих 5 участков по их квалификации (тарифному разряду)

Найти моду по приведенным данным.

Решение:

По максимальной частоте найдем соответствующую группу и варианту: fmax=8 → Мода=4 разряд. Наиболее часто встречающийся разряд рабочих 4.

Определить медиану по данным таблицы.

Как рассчитать медиану? Прежде всего найдем медианный интервал по накопленной частоте. Нужная накопленную частоту. Накопленная частота определяется путем суммирования частот f до тех пор, пока очередная накопленная частота впервые не превысит половину совокупности n+1/2 или n/2.

Для четного ряда 20/2= 10→S= 14 → Ме =4 разряд. Половина всех рабочих имеет тарифный разряд меньше 4, другая половина больше 4.

Формула расчета медианы

Применяемая для расчета медианы формула зависит от типа ряда распределения. Например, в неинтервальном ряду с четным количеством наблюдений медиана будет являться средним арифметическим значением из двух центральных величин, т.е. если совокупность состоит из десяти элементов, то искомый показатель будет равняться среднему значению пятого и шестого элемента. В случае, когда ряд неинтервальный и количество наблюдений нечетное, то медианным будет значение признака, находящегося в центре ранжированного ряда, т.е. для 11 элементов это будет шестой элемент.

В интервальном ряду распределения для вычисления медианы используют следующую формулу:

Формула расчета медианы

где х_О — нижняя граница медианного интервала;

i — ширина медианного интервала;

S_Мe-1 — накопленная частота интервала, предшествующего медианному;

f_Мe — частота медианного интервала.

В том случае, если вариационный ряд является дискретным, то медианным будет величина признака в той группе, в которой накопленные частоты превысили половину количества единиц исследуемой совокупности.

Мода для дискретного и интервального рядов распределения

Мода и медиана во многих случаях оказываются ближе к типичному значению выборки, чем
. Различают определение моды и медианы для дискретного вариационного ряда и для интервального ряда.

Мода — это значение, имеющее в ряду распределения наибольшую частоту, то есть, встречающееся
чаще других. Моду используют, чтобы исследовать спрос населения на различные товары (например, на обувь или одежду),
когда необходимо установить размер, на который отмечен наибольший спрос.

Практический расчет моды зависит от того, для какого ряда распределения она расчитывается:
для дискретного или интервального. Для дискретного ряда моду не нужно вычислять: достаточно найти значение,
имеющее наибольшую частоту. В некоторых случаях с одинаковой высокой частотой в выборке встречаются два
или даже больше значений. Например, если объединить в одну выборку данные обо всех проданных мужских и
женских жакетах, то очень возможно, что встрется два наиболее распространенных размера — две моды. Одна из
них характеризует самый распространенный размер мужского жакета, другая — женского.

Пример 1. В таблице содержатся данные о распределении домашних хозяйств
некоторой территории по числу комнат в жилище. Это дискретный ряд распределения.

	Все	В том числе
В городах	На селе
Все	100,0	100,0	100,0
1 комната	21,0	21,5	19,8
2 комнаты	44,2	46,9	37,7
3 комнаты и более	34,8	31,6	42,5

В городских домашних хозяствах в жилище чаще всего 2 комнаты и, таким образом, мода
для них . В сельских домашних хозяйствах в жилище чаще всего 3 комнаты и
больше и, таким образом, мода для них . Для всех домашних хозяйств мода
.

Для интервального ряда распределения мода рассчитывается по формуле

,

где

— мода;

— нижняя граница модального интервала (интервала с наибольшей частотой);

— ширина модального интервала;

— частота модального интервала;

— частота предмодального интервала;

— частота послемодального интервала.

Пример 2. В таблице содержатся данные о заработной плате и числе
занятых на предприятии N. Это интервальный ряд распределения. Найти моду заработной платы.

Заработная плата, у.е.	Занятых	Накопленные частоты
чел.	%	абсолютные	относительные
18000-22000	10	10,3	10	10,3
22000-35000	28	28,9	38	39,2
35000-45000	25	25,8	63	65,0
45000-60000	18	18,5	81	83,5
60000-80000	13	13,4	94	96,9
80000 и более	3	3,1	97	100,0

Найдём моду заработной платы, используя абсолютные показатели:

Найдём моду заработной платы, используя относительные показатели:

Как видим, результаты совпадают.

Медиана в статистике: понятие, свойства и расчет

Для того чтобы иметь представление о том или ином явлении, мы часто используем средние величины. Их применяют для того, чтобы сравнивать уровень зарплат в различных отраслях экономики, температуру и уровень осадков на одной и той же территории за сопоставимые периоды времени, урожайность выращиваемых культур в разных географических регионах и т. д. Впрочем, средняя является отнюдь не единственным обобщающим показателем – в ряде случае для более точной оценки подходит такая величина как медиана. В статистике она широко применяется в качестве вспомогательной описательной характеристики распределения какого-либо признака в отдельно взятой совокупности. Давайте разберемся, чем она отличается от средней, а также чем вызвана необходимость ее использования.

Медиана в статистике: определение и свойства

Представьте себе следующую ситуацию: на фирме вместе с директором работают 10 человек. Простые работники получают по 1000 грн., а их руководитель, который, к тому же, является собственником, — 10000 грн. Если вычислить среднее арифметическое, то получится, что в среднем зарплата на данном предприятии равна 1900 грн. Будет ли справедливым данное утверждение? Или возьмем такой пример, в одной и той же больничной палате находится девять человек с температурой 36,6 °С, и один человек, у которого она равна 41 °С. Арифметическое среднее в этом случае равно: (36,6*9+41)/10 = 37,04 °С. Но это вовсе не означает, что каждый из присутствующих болен. Все это наталкивает на мысль, что одной средней часто бывает недостаточно, и именно поэтому в дополнение к ней используется медиана. В статистике этим показателем называют вариант, который расположен ровно посередине упорядоченного вариационного ряда. Если посчитать ее для наших примеров, то получится соответственно 1000 грн. и 36,6 °С. Другими словами, медианой в статистике называется значение, которое делит ряд пополам таким образом, что по обе стороны от нее (вниз или вверх) расположено одинаковое число единиц данной совокупности. Из-за этого свойства данный показатель имеет еще несколько названий: 50-й перцентиль или квантиль 0,5.

Как найти медиану в статистике

Способ расчета данной величины во многом зависит от того, какой тип вариационного ряда мы имеем: дискретный или интервальный. В первом случае, медиана в статистике находится довольно просто. Все, что нужно сделать, это найти сумму частот, разделить ее на 2 и затем прибавить к результату ½. Лучше всего будет пояснить принцип расчета на следующем примере. Предположим, у нас есть сгруппированные данные по рождаемости, и требуется выяснить, чему равна медиана.

Источник

Понятие медианы

При анализе различных статистических данных часто возникает необходимость рассчитать различные показатели центра распределения, одним из которых является медиана. Медиана — это один из показателей исследуемого признака, который делит изучаемую совокупность на две равные части, при этом одна часть содержит наблюдения, имеющие значения меньше медианы, а другая состоит из признаков, имеющих значения больше медианного. В силу специфики вычисления медиану считают более достоверной характеристикой типичной величины изучаемого признака, чем, например, средняя арифметическая. Это связано с тем, что рассматриваемый показатель имеет свойство независимости от значений признаков на краях ранжированной совокупности. Нечувствительность к неоднородности изучаемой совокупности и возможным ошибкам выборки при её формировании также называют робастность.