Условия применения параметрических критериев

Проверка экспоненциальности (показательности)

Исключение неизвестного параметра

Положим S_k = X₁ + . . . + X_k, k = 1, . . . , n.

Можно доказать, что для экспоненциального распределения вектор (т.е. выборка Xi-тых заменённая на такую) S₁/S_n, . . . , S_n−1/S_n, распределен так же, как и упорядоченный ряд из равномерного распределения на размера n − 1.

Данное преобразование сводит задачу к проверке равномерности, которую можно решить с помощью критерия Колмогорова. Но за исключение «мешающего» параметра λ приходится платить уменьшением размера выборки на 1.

Критерий Джини (Gini)

Этот критерий базируется на статистике, а по сути индексу Джини:

где X_(i) — это i-ый элемент в упорядоченной по возрастанию выборке (вариационном ряду). Известно, что при верной H величина 12(n − 1)(G_n − 0.5) сходится к нормальному распределению. На этом факте и основан критерий Джини.

Проверка экспоненциальности (показательности)

Для проверки экспоненциальности существует и ряд других критериев (например, Шапиро-Уилка для экспоненциального случая или Андерсона-Дарлинга).

Проверка нормальности

Критерий Шапиро-Уилка (Shapiro-Wilk).

Критерий Шапиро-Уилка базируется на статистике, которая является отношением квадрата линейной оценки стандартного отклонения к смещенной оценке дисперсии:

где a_i — некоторые константы. При верной H распределение SW_n является табличным. На этом факте и основан критерий Шапиро-Уилка.

Критерий Харке-Бера (Jarque-Bera). Этот критерий основан на статистике, которая использует выборочные коэффициенты асимметрии и эксцесса:

где µ_k — центрированный выборочный момент порядка k

Данная статистика сходится к распределению χ2₂. На этом факте и основан критерий Харке-Бера.

Квантильный график

До проверки критериев мы делаем визуальный анализ данных. Согласия хорошо проверять с помощью гистограммы. Но по ней довольно сложно судить о правильности убывания хвостов. Чтобы это проверить был придуман квантильный график

Согласие выборки с распределением, которое образовано с помощью сдвига/масштаба, можно проверить визуально с помощью квантильного графика (Q-Q Plot). К таким распределениям относятся: равномерное, экспоненциальное, нормальное и т.д.

На квантильном графике имеются точки, которые должны расположится вдоль некоторой прямой. Если они располагаются как на графике ниже — тогда у нас отличное согласие.

Условия использования параметрических критериев

Первое условие

Термин «параметрические» используется потому, что в формулу расчета значения критерия включаются параметры распределения, чаще все нормального. Именно поэтому первым условием использования параметрических критериев является нормальное распределение признака.

Поэтому прежде использовать параметрический критерий, в формулу которого включены параметры нормального распределения, необходимо быть точно уверенным, что распределение исследуемого признака соответствует нормальному закону. С этой целью нужно использовать критерии согласия. Если распределение признака не соответствует нормальному закону, для проверки статистических гипотез нужно использовать непараметрические критерии.

Более подробно о методах статистической обработки данных рассказано в книгах:

• Факторный анализ в педагогических исследованиях в области физической культуры и спорта
• Компьютерная обработка данных экспериментальных исследований
• Информационные технологии в обработке анкетных данных в педагогике и биомеханике спорта

Второе условие

Вторым условием является непрерывное распределение признака (случайной величины). То есть, использовать параметрические критерии можно только если распределение признака непрерывно.

Поясним это условие. Известно, что распределение случайных величин может быть и дискретным или непрерывным.

Случайная величина называется дискретной если множество ее значений конечно или счетно (может быть занумеровано натуральными числами, т.е.1,2,3 и т.д.). Например, количество попаданий в кольцо из 10 штрафных бросков (конечное) или количество отжиманий (счетное).

Случайная величина называется непрерывной, если она может принимать любые значения из некоторого промежутка. Число значений непрерывной случайной величины бесконечно. Например, признак рост является непрерывной случайной величиной.

Третье условие

Третьим условием применения параметрических критериев является статистическая шкала, в которой представлены экспериментальные данные. Существуют четыре статистических шкалы: номинальная, порядковая, интервальная и шкала отношений.

Параметрические критерии можно применять к данным, представленными в интервальной шкале и шкале отношений, то есть экспериментальные результаты должны измеряться  в кг, м, с (система СИ) и т.д. Если результаты эксперимента представлены в баллах (это порядковая статистическая шкала) использовать параметрические критерии нельзя. В этом случае необходимо применять непараметрические критерии.

Критерий Уилкоксона

Начнем знакомство с непараметрических тестов для зависимых выборок. Прежде всего стоит отметить, что выборки называются зависимыми, когда испытуемые одной и той же группы были протестированы в разные моменты времени с меняющимися (1) или неменяющимися (2) условиями эксперимента. В первом случае проверяется эффект какого либо действия в сравнении с контрольным измерением («до и после»), во втором — повторяемость результатов эксперимента («контроль-повтор»).

Тест Уилкоксона (от английского «Wilcoxon signed-rank test») является широко используемым и эффективным методом выявления различий между медианами двух зависимых выборок с распределением данных отличным от нормального. Он идеально подходит для сравнения маленьких выборок, где количество испытуемых/исследований больше 5, но меньше 50. Как и для всех критериев, рассмотренных в этой статье, данные могут быть как количественными, так и порядковыми. Метод был разработан в 1945 году американским статистиком и химиком Фрэнком Уилкоксоном (фото справа).

Чтобы запустить тест Уилкоксона в среде R следует загрузить данные выборок и ввести следующую команду:

Как и в t-тесте, в непараметрических статистических тестах внутри скобок можно добавить дополнительные параметры, такие как alternative, conf.int, conf.level. Чтобы посмотреть все аргументы функции, поставьте перед ней знак вопроса, в нашем случае: ?wilcox.test

Непараметрические критерии сдвига

Проверяется гипотеза сдвига, согласно которой распределения двух выборок имеют одинаковую форму и отличаются только сдвигом на константу.
Пусть заданы две выборки
,взятые из неизвестных непрерывных распределений и соответственно.

Нулевая гипотеза:

Наиболее частая альтернативная гипотеза: .

Существует большое количество критериев, проверяющих эту гипотезу:

Быстрый критерий Кенуя

Ранговые критерии сдвига для двух выборок:

• Быстрый ранговый критерий
• Критерий Уилкоксона-Манна-Уитни
• Критерий Фишера-Йэйтса-Терри-Гёфдинга
• Критерий Ван дер Вардена
• Медианный критерий
• Критерий Хаги
• E-Критерий

Ранговые критерии сдвига для нескольких (k>2) выборок:

• Критерий Краскела-Уоллиса
• Критерий Ван дер Вардена
• Медианный критерий
• Критерий Левиса
• Критерий Краузе
• Критерий Пейджа
• Критерий Вилкоксона-Вилкокс
• Критерий Фишера-Йэйтса-Терри-Гёфдинга
• Быстрый критерий Кенуя
• Критерий Джонкхиера
• Критерий Неменьи
• Критерий Фридмена-Кендалла-Бэбингтона-Смита
• Критерий Хеттманспергера
• Критерий Андерсона-Каннемана-Шэча
• Критерий со взвешенными ранжировками Даны Квейд
• Критерий Кендалла-Эренберга
• Критерий Ходжеса-Лемана-Сена

Параметрический критерий

Параметрический критерий 0, как и критерий б в уравнении ( 4 — 24), определяет увеличение коэффициента теплоотдачи за счет уменьшения толщины пограничного слоя с повышением температуры облучателя.
 

Параметрический критерий wjwK представляет собой отношение влажности материала в периоде падающей скорости сушки к критической влажности материала и учитывает уменьшение коэффициента теплоотдачи с уменьшением влажности материала в этот период.
 

Параметрический критерий / Cc ( ci — с2) ср для влажного воздуха может быть заменен двумя критериями К. Kd — di, где MI и Af2 — молекулярные веса бинарной смеси ( сухого воздуха и пара); d — вла-госодержание.
 

Параметрические критерии получаются не как результат обработки основных уравнений, а вытекают непосредственно из постановки задачи. Действительно, обе величины, входящие в параметрический критерий, содержатся непосредственно в условиях задачи, причем либо они обе определены по условиям, либо одна из них рассматривается как искомая.
 

Параметрический критерий р р2 / рь как указывалось, характеризует влияние соотношения между инерционными силами дискретной и несущей фаз.
 

Параметрический критерий K h / R характеризует относительную высоту цилиндра. При / с1 цилиндр можно рассматривать как диск, основания которого поддерживаются при постоянной температуре, а боковая поверхность обменивается теплом с окружающей средой иной температуры.
 

Параметрические критерии распознавания выборок требуют, чтобы исследуемые случайные величины были распределены по некоторому известному закону, обычно по нормальному. Однако, как правило, вид распределений не всегда известен.
 

Параметрическим критерием является отношение одноименных физических величин натурного объекта и модели.
 

Поэтому параметрические критерии могут быть применены только к наблюдениям, которые допускают использование шкал этих двух видов.
 

Наиболее часто параметрические критерии значимости ( — отношение Стьюдента и критерии дисперсионного анализа) применяются в том случае, когда переменные соответствуют интервальной или еще более высокой шкале. Однако такие критерии всегда основываются на предположении о нормальном распределении исходных совокупностей. Вместе с тем иногда исследователь имеет основание сомневаться в обоснованности этого предположения. В таких ситуациях он должен рассматривать в качестве приемлемых альтернатив непараметрические критерии значимости, описанные в этой главе.
 

Применение параметрических критериев может иметь преимущество как с точки зрения возможности определения искомой величины, так и с точки зрения приложения полученных критериальных зависимостей для инженерной практики.
 

Удельное влияние критериев подобия в период падающей скорости сушки на потенциалы переноса.

Влияние параметрического критерия V на распределение температуры и массосодержания существенно, поэтому до 6 0 7 иРо 2 5 при обработке экспериментальных данных его необходимо учитывать в обязательном порядке.
 

Число параметрических критериев гп равно числу пар одноименных величин.
 

К параметрическим критериям относится критерий Стьюден-та и др. В качестве непараметрических А.
 

В чем отличия параметрического критерия от непараметрического?

Параметрические и непараметрические критерии – это два разных подхода к анализу данных. Их основное отличие заключается в том, что параметрические критерии требуют определенных предположений о распределении данных, тогда как непараметрические не имеют таких ограничений.

Параметрический критерий предполагает, что данные имеют определенное нормальное распределение, что позволяет использовать различные статистические методы для обработки данных. Но при наличии нетипичных выбросов, сильно искаженных данных, несоблюдении предполагаемых распределений, параметрические критерии сильно ошибаются.

Непараметрический критерий, напротив, не требует предположений о распределении данных и может быть использован для любых типов данных. Этот критерий ориентирован на выявление различий между двумя или более наборами данных с помощью ранжирования, или сравнения медиан. Непараметрические критерии гораздо менее чувствительны к выбросам, иные аномалиям в данных.

Однако, выбор между параметрическим и непараметрическим критерием зависит от типа данных, целей и постановки задачи и других факторов. Критерии могут сочетаться для улучшения качества анализа в зависимости от цели и уточнения данных.

Сравнение параметров экспоненциальных распределений

Сравнение двух параметров

Предположим, имеются две выборки из экспоненциальных распределений: т.е. из распределений с плотностями . Здесь — параметры распределений (средние значения). Иногда на практике (задачи анализа надежности объектов) используют параметр — интенсивность отказов.

• Критерий Фишера
• Двухвыборочный пуассоновский критерий

Сравнение нескольких (k>1) параметров

• Критерий Дэвида
• Критерий максимального правдоподобия
• Критерий Нагарсенкера
• Критерий Чена
• Комбинированный критерий Сингха

Литература

1. Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006.
2. Лагутин М. Б. Наглядная математическая статистика. В двух томах. — М.: П-центр, 2003.

• Проверка статистических гипотез — о методологии проверки статистических гипотез.
• Статистика (функция выборки)
• Критерии согласия

Параметрический или непараметрический критерий различия?

Статистические методы, использующие параметры нормального распределения данных (среднее, стандартное отклонение и прочее) называются параметрическими. Так например, рассмотренный в предыдущей статье t-тест является типичным параметрическим методом. Почему? Потому, что главным условием для его проведения является нормальное распределение количественных данных. Непараметрические методы, напротив, не зависят от распределения данных и позволяют работать как с количественными, так и с порядковыми данными (например: размер обуви, шкала силы землетрясений).

При нормальном распределении данных параметрические критерии имеют большую мощность по сравнению с непараметрическими. Однако, когда данные выборок не проходят тесты нормальности (такие, как qqplot и Шапиро тест), непараметрические методы дают более точные предсказания. Особенно они эффективны с выборками небольшого размера (

При выборе критерия следует обратить внимание на две вещи: зависимость данных выборок друг от друга и объем выборок

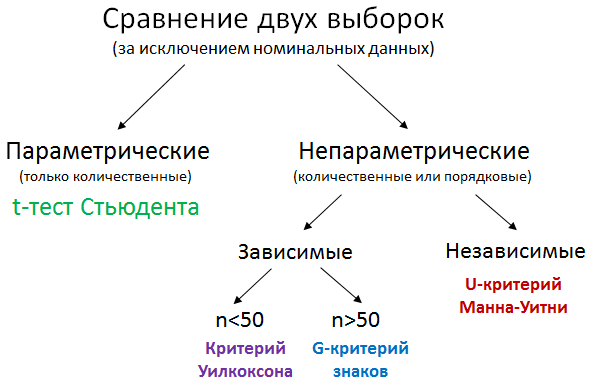
На приведенном выше рисунке Вы видите упрощенную классификацию методов сравнения средних (или медиан) двух выборок. Мы кратко поговорим о каждом из непараметрических критериев, и научимся применять их в среде R. Чтож, приступим!

G-критерий знаков

Если же количество исследований в выборке больше 50, то следует использовать G-критерий знаков. Критерий знаков по статистической мощности уступает Уилкоксону, но превосходит большинство других непараметрических аналогов. Данные выборок должны быть зависимыми, количество исследований в выборке от 5, но не более 300 (про механизм расчетов и ограничения метода можно почитать здесь).

Провести тест в R не сложно, но потребуется сделать несколько манипуляций с данными. Сначала мы загрузим данные двух зависимых выборок, например систолическое (верхнее) давление до и после применения лекарства у 60 пациентов-гипертоников. Загрузим данные «before» и «after» в среду R. Затем визуализируем их.

Затем найдем разность между векторами «before» и «after» и назовем новый вектор «difference», после чего при помощи команды length узнаем его длину. Так как нас интересует, снижает ли лекарство давление у пациентов, мы узнаем какое количество элементов в векторе «difference» больше нуля. Это количество принято называть числом «успехов».

Теперь все готово для того, чтобы запустить G-критерий знаков в R. Для этого воспользуемся командой binom.test, где в параметрах функции укажем сначала число «успехов», затем число исследований в выборке.

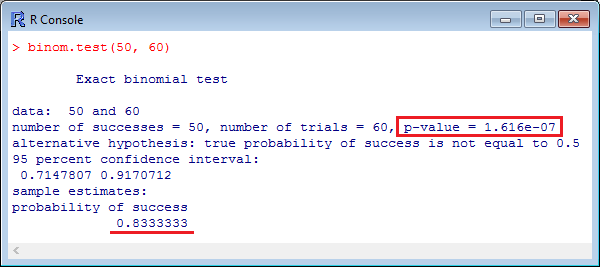
Нулевая гипотеза говорит о том, что медианы выборок статистически не отличаются, альтернативная — что статистические различия есть. В нашем случае p-value значительно меньше 0.05, поэтому мы можем с уверенностью отвергнуть нулевую гипотезу и принять альтернативую: две выборки статистически отличаются друг от друга. Также мы видим, что у 83% пациентов давление снизилось. Для демонстрации статистической значимости результатов эксперимента, просто добавьте к графику надпись p-value < 0.001.

Критерии однородности (A/B тесты)

Критерия однородности, в отличии от критериев согласия, не проверяют согласия выборки с каким-то конкретным распределением, а рассматривают согласие двух выборок, т.е. мы хотим проверить гипотезу, что у них одинаковое распределение.

Например, у нас есть автолюбители, которые предпочитают шины марки А — это будет первая выборка, а есть те, которые без ума от шин марки Б — это будет вторая выборка. Значения в этих выборках — это эффективность работы автомобильных шин (длина тормозного пути, эффективность торможения, шум и т.д.). Требуется выяснить, имеется ли значимое различие эффективности шин А и Б

Есть еще и другой пример: Первая выборка — характеристики до переобувания в зимнюю резину (пусть будут все те же самые, что и выше). Вторая выборка — характеристики после переобувания в зимнюю резину. Требуется выяснить, имеется ли значимое отличие в характеристиках до и после переобувания.

Эти примеры разные в том плане, что в одном случае мы имеем дело с независимым выборкам, а в другом — с зависимыми выборками. Мы будем применять для этих случаев разные критерии.

Параметрические и непараметрические критерии

Параметрические критерии предполагают, что выборка имеет нормальное распределение, т.е. взята из некоторого параметрического семейства распределений. Статистики параметрических критериев более чувствительны к отклонениям от нулевой гипотезы и, в целом, работаю лучше, чем непараметрические (грубо говоря p-value у параметрических обычно ниже, чем у непараметрических критериев)

Но есть одна интересная особенность: непараметрические критерии работают лучше в случае, если совсем немного отходим от нормального распределения. При небольших отклонениях от идеальных условий — они не требуют идеальных условий, например, нормальности данных.

Независимые выборки

Двухвыборочный t-критерий Стьюдента (Уэлча)

Данные критерии основаны на распределении Стьюдента t_k с k степенями свободы называется распределение случайной величины, где в числителе стандартная случайная величина, в знаменателе —  квадратный корень распределения хи-квадрат с k степенями свободы деленный на количество степеней свободы

где X ∼ N (0, 1), Y ∼ χ2_k и являются независимыми.

Плотность распределения Стьюдента с k степенями свободы:

где Γ(u) — гамма-функция Эйлера (специальная функция). Как мы видим, здесь хвосты убывают «тяжелее», чем у нормального распределения

Теорема (Лемма Фишера).Пусть X₁, . . . , X_n — выборка из нормального распределения N (µ, σ2). Обозначим среднее арифметическое по выборке и несмещенную оценку для дисперсии:

Тогда случайные величины X и S2 независимы

• Выборки: X = (X₁, . . . , X_n1), X_i ∼ N (µ₁, σ2₁) и Y = (Y₁, . . . , Y_n2), Y_i ∼ N (µ₂, σ2₂). Выборки могут быть разного размера и имеют нормально распределение. Нюанс: X, Y независимые, σ₁ и σ₂ неизвестны
• Нулевая гипотеза: H : µ₁ = µ₂
• Альтернатива: H₁ : µ₁ ≠ µ₂ или µ₁ > µ₂, или µ₁ < µ₂
• Нулевое распределение: T_n ≈ t_k для некоторого k ∈ N

В целом сравнение средних двух нормальных выборок при неизвестных и неравных дисперсиях известна как проблема Беренса-Фишера. При этом рассмотренная аппроксимация (критерий Уэлча) достаточно точна в двух ситуациях:

• Если выборки одинакового размера n₁ = n₂.
• Если знак неравенства между n₁ и n₂ такой же, как между σ₁ и σ₂,
  то есть выборка с большей дисперсией имеет больший объем.

Критерий Колмогорова-Смирнова

В качестве первого непараметрического критерия можно использовать модификацию критерия Колмогорова (для непрерывных распределений). Например,  две выборки X = (X₁, . . . , X_n) и Y = (Y₁, . . . , Y_n2) с функциями распределения F_X и F_Y соответственно. Обозначим их эмпирические функции распределения и рассмотрим статистику

Если F_X = F_Y , то D_n должна принимать малые значения

При выполнении нулевой гипотезы F_X = F_Y , для любого t > 0 выполняется

где K(t) — функция Колмогорова (при n₁, n₂ ≥ 20 аппроксимация является достаточно точной)

• Выборки: X = (X₁, . . . , X_n1), X_i ∼ F_X и Y = (Y₁, . . . , Y_n2), Y_i ∼ F_y (X, Y независимые; F_X, F_Y непрерывные)
• Нулевая гипотеза: H : F_X = F_Y
• Альтернатива: H₁ : F_X ≠ F_Y

Критерий Манна-Уитни

Критерий Манна-Уитни (или ранговых сумм Уилкоксона) — еще один непараметрический критерий для проверки гипотезы однородности. Он был предложен Уилкоксоном для выборок одинакового размера. Манн и Уитни обобщили его на случай выборок разного размера.

Напомним, что по любой выборке X₁, . . . , X_n всегда можно сопоставить вариационный ряд, то есть упорядочить её по неубыванию:

Рангом наблюдения X_i называется:

• Его позиция в вариационном ряду, если X_i не попадает в связку
• (j₁ + j₂)/2, если x_i попадает в связку от j₁ до j₂; то есть в связке все
  объекты получают одинаковый средний ранг.

Критерий Манна-Уитни основан на следующей статистике V_n:

• Обозначим через R_j ранг порядковой статистики Y_(j), j = 1, . . . , m, в вариационном ряду, построенном по объединенной выборке (X₁, . . . , X_n1, Y₁, . . . , Y_n2).
• Положим V_n = R₁ + . . . + R_n2

• Выборки: X = (X₁, . . . , X_n1), X_i ∼ F_X и Y = (Y₁, . . . , Y_n2), Y_i ∼ F_y (X, Y независимые)
• Нулевая гипотеза: H : F_X = F_Y
• Альтернатива: H₁ : F_X ≠ F_Y
• Статистика: V_n = R₁ + . . . + R_n2
• Нулевое распределение: табличное для малых выборок нормальное приближение для больших выборок