Признаки параллельности двух прямых

Сумма углов многоугольника

Сумма углов произвольного n -угольника вычисляется по формуле:

S n = 180 ° ⋅ ( n − 2 )

где n – это количество углов в n -угольнике.

Пользуясь этой формулой, можно вычислить сумму углов для произвольного n -угольника.

Сумма углов треугольника: S 3 = 180 ° ⋅ ( 3 − 2 ) = 180 °

Сумма углов четырехугольника: S 4 = 180 ° ⋅ ( 4 − 2 ) = 360 °

Сумма углов пятиугольника: S 5 = 180 ° ⋅ ( 5 − 2 ) = 540 °

Так можно продолжать до бесконечности.

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.

На рисунках изображены примеры правильных многоугольников:

Чтобы найти величину угла правильного n -угольника , необходимо сумму углов этого многоугольника разделить на количество углов.

α n = 180 ° ⋅ ( n − 2 ) n

Окружность

Окружность – это замкнутая прямая на плоскости, все точки которой равноудалены от центра (например, обруч)

Дуга – это часть окружности, заключённая между двумя точками, лежащими на этой окружности

В окружности можно провести радиус, диаметр и хорду

Радиус – расстояние от центра до окружности

Диаметр – прямая, соединяющая две точки на окружности и проходящая через центр окружности

Хорда – прямая, соединяющая две любых точки окружности

Также в окружности есть два вида углов

Вписанный угол – угол, у которого вершина лежит на окружности, а стороны угла пересекают её. Такой угол равен половине дуги, на которую опирается

Центральный угол – угол, у которого вершина находится в центре окружности, а стороны угла пересекают её. Данный угол равен дуге, на которую опирается

Окружность, вписанная в четырёхугольник

Чтобы вписать окружность в четырёхугольник, суммы длин противоположных сторон четырёхугольника должны быть равны

              a + c = b + d

У вписанной в прямоугольный треугольник окружности радиус вычисляется по формуле r

Окружность, описанная около четырёхугольника

Чтобы описать окружность около четырёхугольника, необходимо и достаточно выполнения одного из условий:

1. Сумма противоположных углов треугольника равна 180 градусов
2. Вписанные углы, опирающиеся на одну хорду, равны

Окружность, описанная около прямоугольного треугольника

1. Диаметр окружности равен гипотенузе вписанного треугольника
2. Радиус описанной окружности равен половине гипотенузы

R=c/2, где c-диаметр

Что такое горизонтальная линия? Определение, уравнение, примеры, факты

Что такое горизонталь?

Что ты видишь?

В наличии стояк линейка , стоячая отвертка и вертикальный термометр.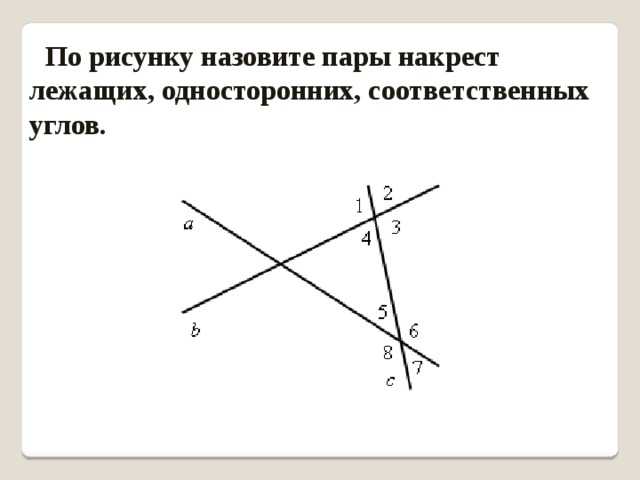

Что ты сейчас видишь?

На полу лежит спальная веревка, отвертка и термометр лежат на полу.

То, что вы видите, описывается как ГОРИЗОНТАЛЬНОЕ положение или объекты, расположенные горизонтально.

Спящая линия — это не что иное, как горизонтальная линия.

A отвертка горизонтальное положение аналогично лестнице, лежащей горизонтально.

A термометр лежать на полу — то же самое, что человек, лежащий горизонтально на полу.

Горизонтальность противоположна вертикали. В геометрии мы используем слова «вертикальный» и «горизонтальный» для обозначения стояния и сна соответственно.

Линия, на которой кажется, что земная поверхность встречается с небом, называется горизонтом. Все, что параллельно горизонту, называется горизонтальным.

Поскольку вертикаль противоположна горизонтали, все, что образует угол 90 градусов (прямой угол) с горизонталью или горизонтом, называется вертикальным.

Итак, горизонтальная линия проходит слева направо.

Использование горизонтали и вертикали в математике

Складываем и вычитаем по горизонтали и вертикали.

Пример 1:

Добавьте 24 и 33 по горизонтали и вертикали.

СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ — Без Сменки

30 июня, 2022

1 мин

Мтмт

Геометрия начинается не с точек или прямых, а с углов. Когда две прямые пересекаются в одной точке появляются углы. И они обладают определёнными названиями и свойствами.

Углы лежащие по одну сторону от какой-то прямой называются смежными и равны в сумме 180 градусам. А углы, которые лежат друг напротив друга называются вертикальными и равны друг другу.

Если у нас внезапно есть две параллельные прямые, и мы каким-то магическим образом пересекаем их третьей, то получаются знаменитые углы при параллельных прямых

В школе было важно не запутаться в их названиях, а в ЕГЭ важно вспомнить какие из них равны, а какие в сумме дают 180 градусов. Есть один простой способ запомнить это раз и навсег… ну как получится, попытка не пытка

️ Посмотрите на углы сверху и снизу, это ведь 2 случая углов при пересечении прямых. Вот у нас повыше был один случай, а тут целых два. То есть с половиной углов мы уже разобрались, теперь решаем, как они связаны между собой. Попробуем наложить верхний угол на нижний и, о чудо, смотрите они сошлись идеально. Углы которое совместились и равны между собой. Вот и все.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!

Редакция Без Сменки

Честно. Понятно. С душой.

44
подписчиков

+ Подписаться

Редакция Без Сменки

01 июля, 2022

1 мин

Хим

Химические свойства фенола

Фенол обладает слабыми кислотными свойствами!

Взаимодействие с щелочными металлами
2С₆H₅OH. ..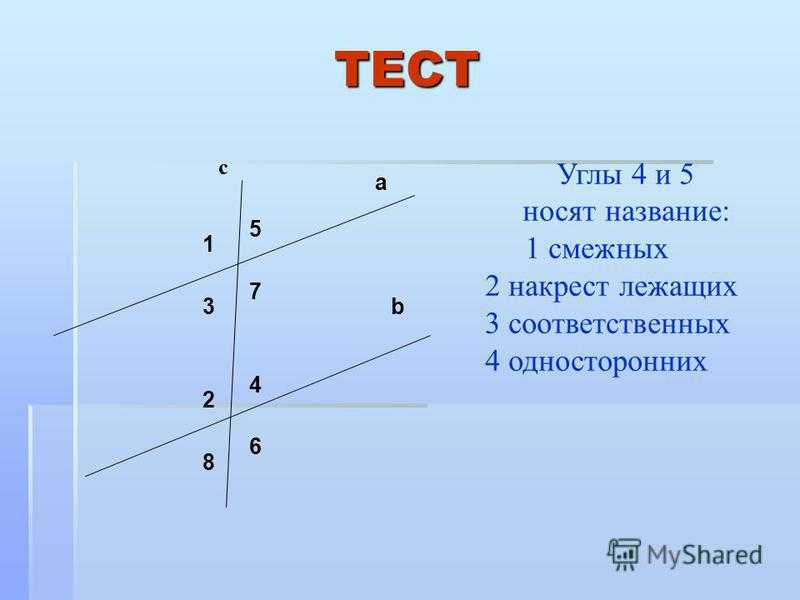

Редакция Без Сменки

30 июня, 2022

1 мин

Мтмт

Виды углов

Каждый угол, в зависимости от его величины, имеет своё название:

Острый — Меньше 90°.
Прямой…

Редакция Без Сменки

29 июня, 2022

1 мин

Физ

Средняя квадратичная скорость

Принято считать, что все молекулы идеального газа двигаются с одинаковой скоростью, которую…

Редакция Без Сменки

28 мая, 2022

1 мин

Общ

Федеративное устройство РФ

В области государственно-территориального устройства Россия является федерацией и состоит из 85. ..

Признаки параллельности прямых: накрест лежащие углы

Очевидно, что проведение секущей — это специальный геометрический метод для определения параллельности прямых. По тому, являются ли те или иные пары углов, образованные секущими, равными, можно заключать о параллельности или непараллельности прямых. Одна из таких пар — накрест лежащие углы.

Доказательство. Проведем прямые $a,$ $b$ и секущую $c$, пересекающую прямые в точках $A$ и $B$ соответственно. По условию прямые образуют с секущей пару равных накрест лежащих углов$\angle{1}$ и $\angle{2}$. Воспользуемся методом от противного и предположим, что прямые не параллельны. Тогда они будут пересекаться в некоторой точке $C$. Отложим на продолжении отрезка $CB$ отрезок $BD$, равный отрезку $AC$.

Треугольники $\bigtriangleup{CAB}$ и $\bigtriangleup{DBA}$ равны по первому признаку равенства треугольников: $AB$ — общая сторона, $BD=AC$ по построению, углы $\angle{1}$ и $\angle{2}$ равны по условию о накрест лежащих углах. Следовательно $\angle{CBA}$ и $\angle{DAB}$ также равны.

Известно, что сумма смежных углов равняется $180^\circ$. Значит, $\angle{CBA}+\angle{DBA}=180^\circ$. Однако сумма равных им углов $\angle{DAB}+\angle{CAB}$, то есть угла $\angle{CAD}$ в $\bigtriangleup{DAC}$, меньше $180^\circ$. Мы пришли к противоречию.

Следовательно прямые параллельны. Теорема доказана.

Внешние накрест лежащие углы!

Заметьте, что при доказательстве мы опирались на равенство внутренних накрест лежащих углов, хотя, если взять признак параллельности прямых, тексте теоремы указана общая формулировка — «накрест лежащие углы», без обозначения их расположения относительно полуплоскостей прямых.

Ответ прост: если доказать признаки параллельности прямых, опираясь на равенство внутренних накрест лежащих углов, внешнее расположение — не более чем условность.

Возьмем для примера $\angle{B}$ и $\angle{H}$. Для $\angle{B}$: внешний $\angle{D}$ — с ним вертикальный; внешний $\angle{C}$ — смежный. Аналогично для $\angle{H}$: $\angle{F}$ и $\angle{E}$ соответственно.

Вертикальные углы равны, поэтому получаем равенство $\angle{D}$ и $\angle{F}.$ У равных углов смежные с ними углы также будут равны, отсюда $\angle{C}=\angle{E}$. Поэтому теорема обычно доказывается по внутренним накрест углам, ведь равенство таких же внешних — прямое следствие.

Признаки параллельности прямых: задача

Отрезки $AB$ и $CD$ пересекаются в общей середине $O$. Докажите, что прямые $AC$ и $BD$ при этом параллельны.

Дано:$AB, CD$$AO=OB$$CO=OD$

Найти: $AC\parallel{BD}$

РешениеРассмотрим треугольники $\bigtriangleup{AOC}$ и $\bigtriangleup{BDO}$. Они равны по первому признаку: по условию $AO=OB$ и $CO=OD$, углы $\angle{COA}$ и $\angle{BOD}$ равны как вертикальные. Следовательно $\angle{ACD}=\angle{BDC}$. Данные углы являются внутренними накрест лежащими. Тогда $AC\parallel{BD}$ согласно признаку параллельности по накрест лежащим углам.

Углы и прямые

Давайте детально рассмотрим углы

Элементы угла

Виды углов и их градусная мера

Существует четыре вида углов.

Смежные и вертикальные углы

Смежные углы – это два угла, у которых одна общая сторона, а две другие лежат на одной прямой. Такие углы в сумме дают 180.

Вертикальные углы – это углы, вершиной которых является одна и та же точка, стороны одного такого угла являются продолжениями сторон другого такого угла. Вертикальные углы всегда равны.

Теперь давайте перейдём к прямым и их расположению на плоскости.

Пересекающиеся и параллельные прямые

Пересекающиеся прямые – это прямые, у которых есть одна общая точка.

Перпендикулярные прямые – это прямые, пересекающиеся под прямым углом. Такие прямые образуют четыре прямых угла при пересечении.

А что такое параллельные прямые?

Параллельные прямые – это прямые, не имеющие ни одной общей точки.

Параллельные и перпендикулярные прямые можно встретить не только в планиметрии, но и в повседневной жизни, например, рельсы и шпалы.

Одинаковы ли прямые?Какие могут быть прямые на плоскости?

Альтернативные внутренние углы — ChiliMath

Пара несмежных углов, которые лежат между двумя прямыми, но находятся на противоположных сторонах поперечной, называются альтернативными внутренними углами .

Чередующиеся внутренние углы образуются при пересечении секущей двух параллельных или непараллельных прямых. Один из способов помочь вам идентифицировать эту пару углов — внимательно посмотреть на слова «альтернативный» и «внутренний».

Альтернативный говорит вам, что углы лежат на противоположные стороны поперечной. Внутренняя , с другой стороны, означает, что углы лежат на внутренней стороне двух линий.

На приведенной выше диаграмме угол 3 и угол 6 расположены с внутренней стороны или между линиями k и m. Они также находятся на противоположных сторонах трансверсали и не примыкают друг к другу. Следовательно, \угол 3 и \угол 6 являются парой альтернативных внутренних углов.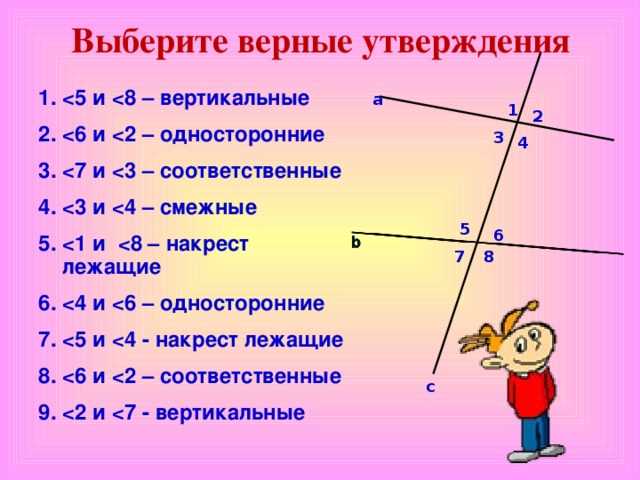 Другая пара — \угол 5 и \угол 4.

СОВЕТ: Вы можете легко определить пару чередующихся внутренних углов, потому что они образуют Z-образную форму или обратную Z-образную форму, как вы можете видеть на рисунках ниже.

Альтернативные внутренние углы Теорема

Если две параллельные прямые пересечены секущей, то пары альтернативных внутренних углов равны .

Здесь у нас есть поперечная t, пересекающая прямые c и w. Так как противоположные внутренние углы равны, оба угла имеют одинаковую меру.

Однако, если секущая пересекает две непараллельные прямые, образующиеся пары чередующихся внутренних углов не равны и не имеют никакого отношения друг к другу.

Примеры задач с альтернативными внутренними углами

Пример 1 : Перечислите все пары альтернативных внутренних углов.

Сразу видно, что углы \angle 1, \angle 8, \angle 5 и \angle 4 расположены на внутренней стороне наших двух линий, линий h и s.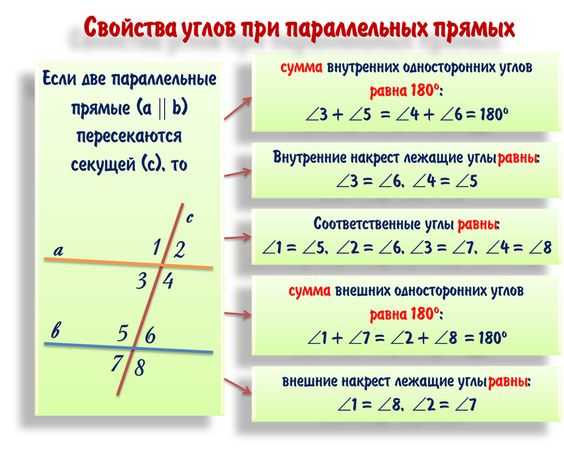 Это наши внутренние углы.

Но так как нас просят определить пары чередующихся внутренних углов, давайте рассмотрим пары внутренних углов, несмежных и находящихся по разные стороны от трансверсали, т.е. Итак, мы имеем

• \угол 1 и \угол 4
• \угол 8 и \угол 5

Пример 2: Заполните пропуски, чтобы сделать следующие утверждения верными.

Углы, образующиеся при пересечении прямых

Чтобы понять, как выглядят соответственные углы, а также уметь находить их на любых геометрических рисунках, нужно хорошо усвоить разницу между типами фигур, образованных секущей линией

Кроме того, следует обратить внимание на наличие внутренней и внешней областей. Первая зона ограничивается площадью между двумя прямыми, второй внешней областью считается неограниченное пространство снаружи от этих двух линий

Итак, образованным тремя прямыми линиями угловым фигурам можно дать следующие определения:

• Накрест лежащие внутренние углы — это разносторонние по отношению к секущей объекты внутри области, сформированной прямыми. Если обе фигуры лежат за пределами двух прямых по противоположные стороны от секущей, то такие угловые элементы называются внешними накрест лежащими.
• В отличие от предыдущих противолежащих фигур, односторонние углы расположены на одной стороне: внутри области, образованной двумя прямыми (внутренние), или во внешних областях (наружные).
• Соответственные по определению являются парными фигурами, образующимися по одну сторону от линии, пересекающей две других, с аналогичных сторон обеих прямых. Один из углов пары расположен между прямыми и является внутренним, а другой лежит вне этой зоны, поэтому считается внешним.

Чтобы окончательно разобраться в вопросе, нужно усвоить понятие соответствия с математической точки зрения. В геометрии это свойство двух фигур, у которых углы, стороны или точки одного объекта аналогичны соответствующим элементам другого объекта. Аналогия проявляется не в их равенстве, а во взаимном соотношении элементов. О соответствии углов говорит аналогичное пространственное положение лучей в местах пересечения прямых с третьей секущей линией. Таким образом, речь идет об элементах, имеющих одинаковое относительное положение.

Следствие из свойства прямых

На прямую а может быть опущен единственный перпендикуляр из любой точки А, которая не принадлежит данной линии. Доказательство утверждения состоит из следующих шагов:

Вначале следует отметить на прямой а произвольную точку, обозначив ее С1.
Далее можно провести через С1 линию с, перпендикулярную а.
Затем через точку А нужно начертить АС2, которая параллельна с.
После этого следует предположить о существовании перпендикуляра, который вместе с АС2 пересекает линию а с образованием третьего отрезка АС3.

Поскольку из точки А нельзя проводить перпендикуляр АС3 и править треугольник АС2С3, дополняя его другим перпендикулярным отрезком, то согласно свойству параллельных прямых АС2||АС3.

Если односторонние углы не прямые, то один из них является острым, а другой — тупым, то есть меньшим или большим по величине. Если через каждый из них провести биссектрисы, то они должны пересечь противоположные стороны в определенных точках. Для этого достаточно отложить отрезки на параллельных линиях, равные AB, используя циркуль.

Секущая и отрезки, принадлежащие проведенным биссектрисам, образуют 2 треугольника вместе с параллельными. Напротив большего угла будет находиться биссектриса, отсекающая наибольший отрезок. Это подтверждает теорема о соотношении между углами и сторонами разностороннего треугольника.

Соединив точки пересечения биссектрис с параллельными прямыми, можно построить четырехугольник ABCD. Чтобы доказать, что полученная фигура является параллелограммом, достаточно учесть следующее:

По построению AB=BD=AD.
Следовательно, AB=CD.
Точки C и D равноудалены от A и B.
Отрезки AB и CD параллельны.

«Признак» или «теорема»?

Все доказанные признаки параллельности прямых так или иначе в научном понимании является теоремами. При этом, тем не менее, в формулировках слово «теорема» не фигурировало: мы все время пользовались обозначением «признак».

Причина здесь — амбивалентность, создаваемая словосочетанием «теорема параллельности».  Есть аксиома параллельности, а есть, значит, еще и теорема? Тогда аксиома совсем не аксиома, если ей можно противопоставить теорему параллельности. Замена «теорема» на «признак» разрешает данную двойственность.  

Есть, конечно, еще одна причина… Но это разговор для целого отдельного урока. Этот урок, к слову, следующий. Загляните.

{"questions":,"answer":}}}]}

Методы вычисления

Зная значение любого из накрест лежащих, односторонних и соответственных углов, можно найти величины всех остальных, воспользовавшись их свойствами. Для проведения вычислений проще всего воспользоваться векторной формой представления прямых.

Пусть существует две параллельных линии, которые заданы следующим образом:

• A (x, y) = A0 (x1, y1) + k*(a1, a2);
• B (x, y) = B0 (x2, y2) + w*(b1, b2).

Секущая задается векторным уравнением: C (x, y) = С0 (x3, y3) + l*(c1, c2). Для расчета угла пересечения любых двух прямых необязательно искать их общую точку, достаточно воспользоваться свойствами умножения направляющих векторов. Они могут перемножаться двумя различными способами:

Пусть следует найти угол пересечения прямых A и C. Для скалярного произведения можно записать: ((a1, a2)*(c1, c2)) = a1*c1 + a2*c2 = ((a1)^2+(a2)^2)^0,5*((c1)^2+(c2)^2)^0,5*cos (teta). Откуда получается неизвестный угол teta:

teta = arccos ((a1*c1 + a2*c2)/(((a1)^2+(a2)^2)^0,5*((c1)^2+(c2)^2)^0,5)).

Другой способ определения teta заключается в применении векторного произведения. Получается следующее выражение: = a1*c2 — a2*c1 = ((a1)^2+(a2)^2)^0,5*((c1)^2+(c2)^2)^0,5*sin (teta). Тогда teta может быть вычислен по формуле:

teta = arcsin ((a1*c2 — a2*c1)/(((a1)^2+(a2)^2)^0,5*((c1)^2+(c2)^2)^0,5)).

Вычислить соответствующие функции арксинуса или арккосинуса можно с использованием инженерного калькулятора. Как только известен угол пересечения секущей и параллельной прямых, остальные углы находятся с помощью добавления или вычитания его из 180 градусов, согласно их свойствам.

Свойства смежных углов

1. Сумма смежных углов равна 180°

2. Если оба смежных угла равны между собой, то они являются прямыми.

3. В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.

4. Синусы смежных углов равны.

5. Косинусы, тангенсы и котангенсы смежгых углов равны, но имеют противоположный знак.

Справедливость пунктов 2 и 3 очевидны и следуют из (1).

Доказательство пункта 4. Обозначим через α один из смежных углов. Тогда величина другого угла будет равна 180°−α. Но (см. статью Формулы приведения тригонометрических функций онлайн)

.

То есть синусы смежных углов равны.

Доказательство пункта 5. Обозначим через α один из смежных углов. Тогда величина другого угла будет равна 180°−α. Но

,

,

.

То есть косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.

Изучаемый геометрический объект

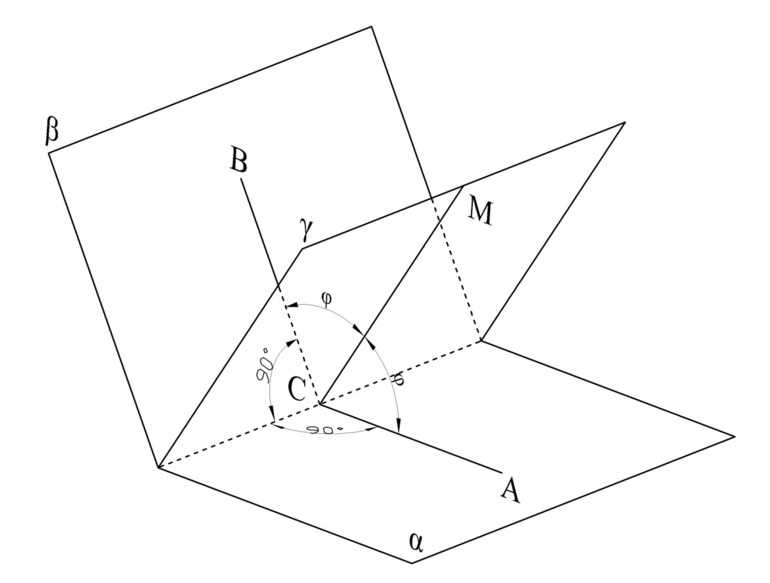
Прежде чем рассматривать углы, которые образуются в результате различного взаимного расположения прямых на плоскости, следует подробно изучить сам геометрический объект. Любая прямая линия представляет собой набор точек в пространстве любой мерности, каждая из которых может быть получена из предыдущей путем ее переноса на вектор, имеющий конкретное направление.

Векторное представление

Определение прямой говорит о том, что для универсального ее математического описания следует воспользоваться понятием вектора. Под ним в математике подразумевают направленный отрезок, имеющий начало и конец. В двумерном пространстве любой вектор представляется набором двух чисел, например, a (a1, a2). Построить его можно следующим образом:

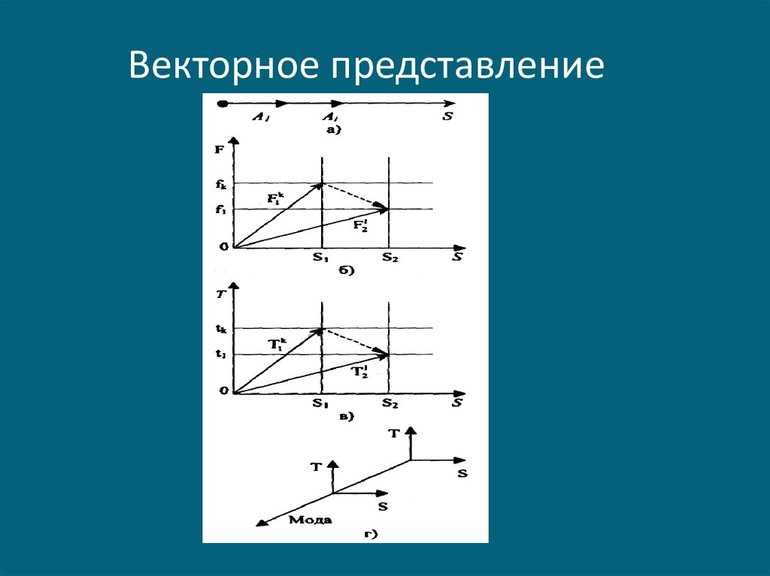
Необходимо начало вектора расположить в точке (0, 0) (пересечение осей абсцисс и ординат в декартовой системе).
Конец направленного отрезка помещается в точку с координатами (a1, a2).
Начало и конец соединяются так, что стрелка (направление) указывается в точку (a1, a2).

Самостоятельно вектор не может задать прямую, поскольку существует бесконечное множество объектов a (a1, a2), которые получаются с помощью параллельного переноса их по всей плоскости. Необходима фиксированная точка, чтобы привязать начало направленного отрезка. Так образуется прямая линия. Ее векторное уравнение может быть записано в следующем виде:

A (x, y) = A0 (x0, y0) + alfa*(a1, a2).

Здесь A (x, y) — произвольная точка линии, A0 (x0, y0) — фиксированная точка на ней, (a1, a2) — координаты вектора, который называется направляющим, alfa — любое рациональное число, которое показывает, на какую долю направленного отрезка (a1, a2) следует переместить A0 (x0, y0), чтобы попасть в A (x, y).

Другие формы уравнений

Векторное уравнение прямой является неявным по отношению к координатам x и y. Для одних задач его удобно использовать, для других же следует применять иные формы записи. Одной из них является параметрическая. Ее можно записать так:

Этой формой удобно пользоваться для определения конкретных координат x и y. Если из этой системы равенств выразить параметр alfa, то можно получить симметричное уравнение прямой:

Наконец, если представить это выражение таким образом, чтобы y был выражен, как функция от x, то получится общее представление прямой линии в двумерной системе координат:

y = a2/a1*x + (y0-a2/a1*x0).

Эта формула известна любому школьнику, поскольку основное внимание при изучении геометрических свойств рассматриваемого одномерного объекта в школах уделяется именно ей. Зная, как перевести один вид уравнения прямой в другой, можно выполнять соответствующие преобразования для решения конкретных задач

Рассматривая вопрос параллельных углов, следует изучить все возможные варианты расположения на плоскости прямых линий. Количество ситуаций зависит от числа присутствующих геометрических объектов, а также от размерности координатной системы.

Две прямые

На плоскости существует три разных варианта расположения двух прямых относительно друг друга. К ним относятся следующие:

Совпадение. Два объекта могут иметь разные направляющие вектора и фиксированные точки, но при этом будут накладываться друг на друга. Чтобы это проверить, необходимо взять произвольные две точки, которые принадлежат одной линии, и подставить их координаты в уравнение для другой. Если равенство в обоих случаях будет верным, то прямые являются идентичными.
Параллельность. В этом случае ни одна точка одной прямой не принадлежит другой. Однозначным и достаточным доказательством параллельности является возможность выразить направляющий вектор одного объекта, через направленный отрезок другого путем его умножения на какое-либо рациональное число.
Пересечение. Обе прямые имеют одну общую точку. Чтобы ее найти, следует решить систему уравнений. Для этого удобно воспользоваться общей формулой выражения для прямых.

Три прямые

Когда на плоскости имеются три прямых, то количество вариантов их взаимного расположения возрастает. Возможные следующие случаи:

Пересечение в одной точке.
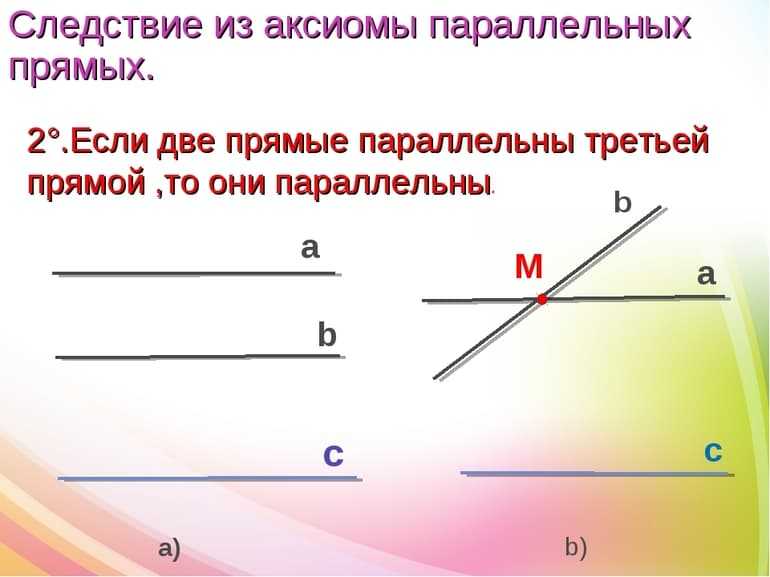
Параллельность двух, которые пересекаются третьей.
Все три параллельны друг другу.

Доказательство подобия треугольников

Существует три признака, по которым могут быть определены подобные треугольники. Во-первых, подобие подтверждается пропорциональностью всех трех сторон треугольников. Во-вторых, подобными считаются треугольники, имеющие две пропорциональные стороны, угловая величина между которыми равна соответствующему элементу второго треугольника. В-третьих, подобие подтверждается, когда имеет место равенство двух углов обоих треугольников.

Рассмотрим доказательство этого признака, в ходе которого применяется свойство тождественности соответственных угловых объектов:

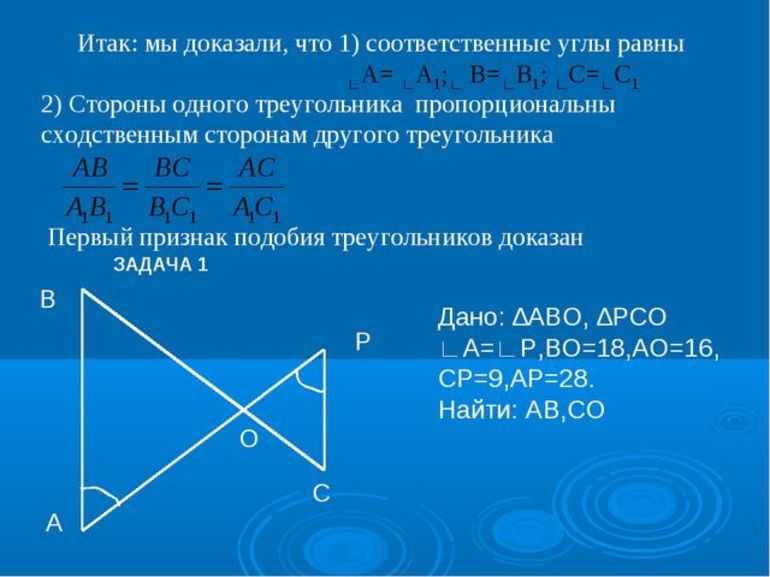
1. Возьмем два треугольника ABC и A1B1C1, в которых равны два угла. Из этого следует, что величина третьего угла также одинакова в обеих фигурах. Требуется доказать подобие треугольников.
2. Отметим точку A2 на AB таким образом, чтобы величина BA2 совпала с A1B1. Через A2 параллельно основанию AC проведем прямую, проходящую через BC в точке B2.
3. Треугольники A2BC2 и A1B1C1 равны, что подтверждается одинаковыми величинами сторон A1B1, BA2 и углов B, B1 (по построению или условию), а также равенством углов A, A1 как соответственных при параллельных линиях.
4. Поскольку, согласно лемме, параллельная стороне треугольника прямая отсекает от него подобный треугольник, то A2BC2 подобен ABC. Из этого следует подобие треугольников ABC и A1B1C1.

В сложных планиметрических фигурах в качестве секущей, формирующей этот тип геометрических объектов, может выступать медиана, биссектриса треугольника или какие-либо другие линии. Для решения таких задач требуется хорошее знание базовых понятий, признаков, свойств, аксиом, позволяющее заметить определенные соотношения и закономерности в том или ином задании.

Соответственные углы при параллельных прямых

Свойства фигур, формирующихся при пересечении секущей параллельных прямых, давно описаны в планиметрии. Известно, что соответственные накрест лежащие угловые элементы при параллельных прямых равны. Сложение угловых величин односторонних фигур дает значение 180 градусов. В геометрии применяется формула для расчета суммы соответственных парных угловых фигур при условии параллельности двух линий. Для определения этого параметра из числа 360 надо вычесть удвоенную угловую величину одностороннего угла, прилежащего к любому из пары рассчитываемых соответственных угловых элементов.

Равные соответственные углы указывают на параллельность прямых. Справедливость этого признака вытекает из следующих утверждений:

1. Отметим отрезок на секущей, начало и конец которого, точки C и D, находятся в местах пересечения секущей с прямыми a и b.
2. Через среднюю точку K отрезка опустим перпендикуляр к прямой a. Точки его пересечения с прямыми обозначим как A и B. Сформированные отрезками треугольники CKA и DKB являются прямоугольными, а отрезки AK и BK — сторонами, прилежащими к прямоугольным вершинам. Каждый из этих катетов одновременно является высотой треугольника, проведенной из остроугольной вершины.
3. Для доказательства следует учитывать равенство вертикальных ∠CKA и ∠DKB, ∠BDK и ∠АСК равны по условию равенства соответственных углов с учетом того, что вертикальные углы с вершинами в точках C и D равны, CK и KD — два равных отрезка по условию.
4. Таким образом, в треугольниках CKA и DKB сторона и прилежащие к ней углы имеют равные величины, что соответствует одному из признаков равенства треугольников.
5. Поскольку AB перпендикулярен прямой a и отрезку AC, то CKA — прямоугольный треугольник, и это дает основание считать, что равный ему треугольник DKB также прямоугольный, из чего следует перпендикулярность отрезка AB по отношению к прямой b.
6. Было доказано, что две прямые перпендикулярны к третьей прямой, и это подтверждает их параллельность.

Такого рода свойства встречаются в описаниях признаков и теорем. Их равенство — часть доказательств равенства и подобия треугольников. В свою очередь, используя признаки подобных и равных треугольников, можно обосновывать доказательства сложных теорем, находить решения сложных задач, править возможные ошибки.

Треугольники, их виды и признаки их равенства

Сумма углов любого треугольника равна 180°

Для треугольников также верно следующее утверждение: каждая сторона треугольника меньше суммы двух других его сторон

Элементы треугольника:

Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Также медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины (в треугольнике медиана показана как BM)

Биссектриса – это отрезок, делящий угол на два равных угла. Также центром вписанной в треугольник окружности является точка пересечения биссектрис углов треугольника (в треугольнике биссектриса показана как BD)

Высота – это перпендикуляр, опущенный из вершины на одну из сторон треугольника. Также высоты или их продолжения пересекаются в одной точке, которая называется ортоцентром (в треугольнике высота показана как ВН)

Средняя линия – это отрезок, соединяющий середины сторон. Средняя линия треугольника параллельна основанию, и по длине она равна половине основания. Средняя линия трапеции равна половине суммы оснований и параллельна основаниям.

Виды треугольников:

У равностороннего треугольника все стороны равны и углы по 600.

У равнобедренного треугольника равны только две стороны и углы при основании. Медиана, проведенная в нём к основанию, также является биссектрисой и высотой. 

У прямоугольного треугольника один угол равен 900 и сумма двух других углов тоже равна 900. Сторона, лежащая напротив прямого угла в таком треугольнике, называется гипотенузой, а две другие — катетами. Катет, лежащий напротив угла 300, равен половине гипотенузы. Медиана, проведённая в прямоугольном треугольнике из вершины прямого угла, равна половине гипотенузы

Фактчек

Равенство треугольников можно определить по одному из трёх признаков равенства треугольников (по двум сторонам и углу между ними, по стороне и прилежащим к ней углам, по трем сторонам).

Признаки подобия немного отличаются от признаков равенства треугольников (по двум сторонам и углу между ними, по двум углам, по трём сторонам), по ним определяется отношение соответственных сторон одного треугольника к сторонам другого.

Для нахождения площади выпуклого четырёхугольника есть универсальная формула S = ½* d1* d2 *sin α , где d 1, d 2 — длины диагоналей четырехугольника, α — угол между диагоналями четырехугольника. 

Окружность можно вписать в четырёхугольник, если суммы его противоположных сторон равны, а описать окружность около четырёхугольника можно, если пара противоположных углов в сумме даёт 180 градусов.

Так же стоит помнить, что в теореме синусов равны не только отношения противолежащих сторон к синусам углов, но и каждое такое отношение равно двум радиусам описанной окружности.