Уравнение изотермы химической реакции примеры

Уравнение изотермы химической реакции примеры

ЛЕКЦИЯ № 5. Химическое равновесие

1. Понятие химического равновесия. Закон действующих масс

При протекании химической реакции через некоторое время устанавливается химическое равновесие. Существует два признака химического равновесия: кинетический, термодинамический. В кинетическом – ?_пр = ?_обр, в термодинамическом – характеризует химическую реакцию при условиях P, t – const (?G = 0); при условиях V, Т – const (?F = 0).

Химический потенциал – функция, которая характеризует состояние i-го компонента при определенных внешних условиях.

где n₁ – число молей i-го компонента.

Если к бесконечно большому количеству раствора прибавить определенное количество какого-нибудь компонента, то химический потенциал системы определяется изменением изобарного потенциала при изобарных условиях или изменением изохорного потенциала при изохорных условиях.

Химический потенциал зависит от концентрации данного компонента

где Р_i– парциальное давление – вклад каждого компонента в общее давление или давление, которое компонент имел бы, если бы находился в смеси.

Парциальное давление – элементарная функция (можно складывать). Пример (O₂, N₂, H₂) – их общее давление

?– значение химического потенциала при стандартных условиях.

Химический потенциал характеризует способность данного компонента выходить из данной фазы путем испарения, растворения, кристаллизации и т. д. Переход этот происходит произвольно.

В результате химического равновесия скорость прямой реакции уменьшается, а скорость обратной реакции увеличивается.

Концентрации, которые соответствуют химическому равновесию, называются равновесными концентрациями. Связь между равновесными концентрациями устанавливается законом действующих масс (ЗДМ). Этот закон в 1867 г. вывели К. М. Гульберг и П. Вааге.

Кинетический вывод ЗДМ

f – фугитивность – парциальное давление для реальных газов. Возникает вопрос, будут ли равняться К_pи К_с.

К_pи К_c– отличаются на RT ?vi в сумме стехиометрических коэффициентов.

если ?v_i = 0, то K_p = K_c. ?v_i = 1 + 1 – 1 – 1 =0 – когда стехиометрический коэффициент = 1.

2. Уравнение изотермы химической реакции

Если реакция протекает обратимо, то ?G= 0.

Если реакция протекает необратимо, то ?G? 0 и можно рассчитать изменение ?G.

где ? – пробег реакции – величина, которая показывает, сколько молей изменилось в ходе реакции. I сп – характеризует равновесное и неравновесное состояние реакции, II сп – характеризует только неравновесные состояния.

это уравнение изотермы химической реакции.

С помощью уравнения изотермы химической реакции можно судить о направлении протекания реакции.

3. Уравнения изохоры, изобары химической реакции

Зависимость К от температуры

По ним судят о направлении протекания реакции:

4. Расчет K_P (метод Темкина-Шварцмана)

термодинамический метод расчета K_p.

Пример. Расчет K_pдля реакции PbS0₄ распадается на РbО и S0₃.

Результаты вычислений занесены в таблицу 2.

5. Расчет равновесного состава химического равновесия

Равновесный состав можно рассчитать только для газовой системы

Исходная концентрация всех компонентов

Изменение каждого компонента по числу молей (или стехиометрическому коэффициенту):

?_?– (пробег реакции) – химическая переменная.

Она показывает изменение количества вещества по числу молей. Если реакция не началась, то ?_? = 0. Если количество исходных веществ превратилось в такое же количество продуктов реакции, то ?_? = 1.

Рассчитать равновесный состав по третьему компоненту при условии, что А = а моль/л; В = в моль/л.

Рассчитываем по 4 компоненту:

Газообразные вещества реагируют по уравнению:

Найти парциальное давление каждого компонента.

Вещества А и В превращаются в С в количестве Х. Исходные вещества А= 2 моль, В= 1 моль.

Для того, чтобы найти парциальное давление, мы должны Р_об умножить на мольную долю. Мольная доля определяется отношением числа молей каждого компонента, отнесенного к общему числу молей всех компонентов.

где E_n– общее число молей, участвующих в этой газовой смеси.

где Р_А – парциальное давление.

Изотерма химической реакции и ее применение для подбора условий проведения реакций

Автор работы: Пользователь скрыл имя, 15 Сентября 2014 в 12:51, реферат

Краткое описание

Уравнение изотермы Вант-Гоффа позволяет рассчитать максимальную работу химической реакции и тем самым определить возможность её самопроизвольного протекания в каких-либо конкретных условиях (при температуре Т и концентрациях реагентов Ci или парциальных давлениях Pi).По условиям проведения реакции делятся на изотермические и неизотермические. Изотермические реакции протекают при постоянной температуре, а неизотермические – при непостоянной температуре. Химическое взаимодействие реагентов может происходить с выделением или без выделения тепла, в связи, с чем и происходит изменение температуры реакции.

1. Введение…………………………………………………………..32. Химическое равновесие в гомогенных системах………………43. Уравнение изотермы Вант – Гоффа…………………………. 64. Правило Вант-Гоффа…………………………………………….85. Литература ……………………………………………………….9

ИЗОТЕРМА ВАНТ — ГОФФА, ВЫВОД И АНАЛИЗ

Константа равновесия определяют условия равновесия, когда концентрация (парциальные давления) является равновесными. В каком направлении пойдёт химическая реакция, если парциальное давление исходных веществ и продуктов реакции отличаются от равновесных? Ответить на этот вопрос поможет уравнение изотермы химической реакции.

Рассмотрим уравнение реакции: aA + bB cC + dD

Для изобарно-изотермического процесса изменение Гиббса равно:

P’- неравновесное, парциальное давление компонентов.

где =

— по форме записи напоминает константу равновесия, но отличается тем, что вместо равновесных давлений в него входят величины давления в данный момент времени.

( ) — это выражение, куда входят величины концентраций в данный момент времени.

АНАЛИЗ ИЗОТЕРМЫ ВАНТ-ГОФФА

1. Главное значение изотермы реакции состоит в том, что она позволяет рассчитать ∆Gили ∆Fобратимый реакции для заданного состава реакционной смеси и определить, в каком направлении, и до какого предела протекает реакция при известных условиях.

а) Если Кр˃Кр’, то lnКр˃lnКр’; ∆G˂0- реакция идет самопроизвольно в прямом направлении.

б) Если Кр˂Кр’, то lnКр˂lnКр’; ∆G˃0- реакция протекает самопроизвольно в обратном направлении, в сторону образования продуктов.

в) Если Кр=Кр’, то lnКр=lnКр’; ∆G=0- равновесие.

Если парциальное давление всех участников реакции в данный момент времени равны атмосферному давлению

Пусть P_A’=P_B’=P_C’=P_D’=1( 1,013*10 5 Па), тоKp’=1; Тогда логарифм этого выражения будет равен нулю (lnKp’=0), а уравнение изотермы Вант – Гоффа примет вид:

∆G⁰=RTlnKp-стандартная энергия Гиббса

Выразм константу равновесия из последнего уравнения и получим:

Пример решения задачи:

В объеме 10л, взяли: 320(г) О₂ , 10(г) Н₂ и 180(г) паров воды . Определите, в какую направлении пойдёт химическая реакция: , если при температуре Т

(Кс=10). Процесс изохорный.

;

;

;

;

;

;

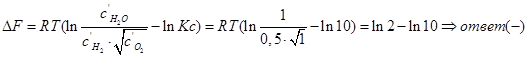
˂0 — реакция идет в прямом направлении.

ВЛИЯНИЕ ВНЕШНИХ УСЛОВИЙ НА КОНСТАНТУ

РАВНОВЕСИЯ. УРАВНЕНИЕ ИЗОБАРЫ И ИЗОХОРЫ ВАНТ-ГОФФА (В-Г)

Константы равновесия — это величины постоянные при данной температуре. При изменении температуры константа равновесия изменяется, и довольно существенно.

Изменение константы равновесия и направления химической реакции в зависимости от температуры количественно характеризует уравнение изобары изохоры химической реакции.

ВЫВОД УРАВНЕНИЯ ИЗОБАРЫ И ИЗОХОРЫ

Разделим уравнение изотермы Вант- Гоффа на температуру:

Продифференцируем его по Т и перепишем:

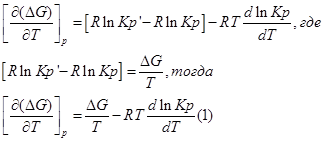
Представим уравнение Гиббса – Гельмгольца в виде:

Из уравнения (1) вычтем уравнение (2):

Эти уравнения показывают влияния температуры на константу равновесия, где определяющим фактором является тепловой эффект химической реакции.

Влияние температуры на константу равновесия определяется типом реакци.

В обратном — Т↓,Кр↓.

2. Если ∆H(∆U)˂0 (экзотермическая, выделение), то ˂0, тогда при повышении температуры константа равновесия Кр уменьшается или Кр увеличивается при понижении температуры.

3. Если ∆H(∆U)=0 , тов этом случае константа равновесия не зависит от температуры Кp ≠ f(T).

ИНТЕГРИРОВАНИЕ ИЗОБАРЫ В-Г

1. Приближенное интегрирование ∆Н ≠ f(Т),

тогда ;

;

;

;

;

.

С помощью этого уравнения можно найти:

1. ∆Н (тепловой эффект реакции), если известны равновесия при двух различных температурах (Кр₁(Т₁) и Кр₂(Т₂))

2. Кр₂(Т₂) – константу равновесия при температуре Т_2, если известна константа равновесия при другой температуре и тепловой эффект реакции (Кр₁(Т₁) и ∆Н).

Так как после интегрирования мы получили уравнение прямой, то эта зависимость может быть представлена на графике: lnKp(1) lnKp(2)

Тангенс угла наклона прямой реакции, исходя из уравнения прямой:

;.

Зависимость теплового эффекта от температуры выражается уравнением:

Подставим это уравнение в уравнение изобары Вант- Гоффа:

;

при Т=0(К)

Проинтегрируем это уравнение и получим:

;

где В — постоянная интегрирования, для нахождения необходимо знать значения константы равновесия Кр при любой фиксированной температуре.

Однако проводить расчеты с использованием данного уравнения довольно сложно и используется довольно редко.

Пример. Определим изменение эффекта реакции Fe+H₂O+FeO+H₂, если для Т₁=900К, Кр₁=1,452, а для Т₂=1025К Кр₂=1,285.

Используем уравнение:

При повышении температуры от 900 до 1025К выделится дополнительно 7,5 кДж/моль теплоты.

|	следующая лекция ==>
Метод статистического моделирования нагрузки на ЭВМ	|	Строение и характеристика макроэргических соединений на примереАТФ

Дата добавления: 2016-02-02 ; просмотров: 9770 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ