Презентация на тему проекции плоскости (лекция 3)

3.7. Перпендикулярность прямой плоскости

Признак перпендикулярности прямой плоскости: прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.

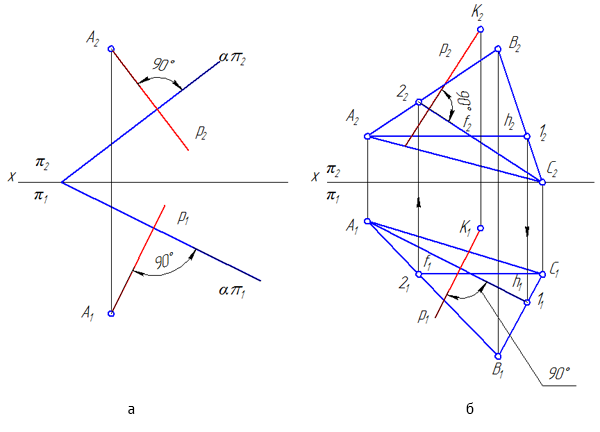
Рисунок 3.16 – Задание прямой, перпендикулярной плоскости

Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)

Теорема доказывается через теорему о проецировании прямого угла в частном случае.

Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).

Пусть прямая p перпендикулярна плоскости σ=ΔАВС  и проходит через точку K.

1. Построим горизонталь и фронталь в плоскости σ=ΔАВС  : σ=ΔАВС : A-1∈σ; A-1//π₁; С-2∈σ; С-2//π₂.
2. Восстановим из точки K перпендикуляр к заданной плоскости: p₁⊥h₁ и p₂⊥f₂, или p₁⊥απ₁ и p₂⊥απ_2.

1.1. Центральное проецирование

Проецирование (лат. Projicio – бросаю вперёд) – процесс получения изображения предмета (пространственного объекта) на какой-либо поверхности с помощью световых или зрительных лучей (лучей, условно соединяющих глаз наблюдателя с какой-либо точкой пространственного объекта), которые называются проецирующими.

Известны два метода проецирования: центральное  и параллельное.

Центральное проецирование заключается в проведении через каждую точку (А, В, С,…) изображаемого объекта и определённым образом выбранный центр проецирования (S) прямой линии (SA, SB, >… — проецирующего луча).

Рисунок 1.1 – Центральное проецирование

Введём следующие обозначения (Рисунок 1.1):

S – центр проецирования (глаз наблюдателя);
π₁ – плоскость проекций;

A, B, C – объекты проецирования – точки;

SA, SB – проецирующие прямые (проецирующие лучи).

Примечание: левой клавишей мыши можно переместить КРАСНУЮ точку в горизонтальной плоскости, при щелчке на точке левой клавишей мыши, изменится направление перемещения и её можно будет переместить по вертикали.

 Центральной проекцией точки называется точка пересечения проецирующей прямой, проходящей через центр проецирования и объект проецирования (точку), с плоскостью проекций.

Свойство 1. Каждой точке пространства соответствует единственная проекция, но каждой точке плоскости проекций соответствует множество точек пространства, лежащих на проецирующей прямой.

Докажем это утверждение.

На рисунке 1.1: точка А₁ – центральная проекция точки А на плоскости проекций π₁. Но эту же проекцию могут иметь все точки, лежащие на проецирующей прямой. Возьмём на проецирующей прямой SA точку С. Центральная проекция точки С (С₁) на плоскости проекций π₁ совпадает с проекцией точки А (А₁):

1. С ∈ SA;
2. SC ∩ π₁=C₁ → C₁ ≡ A₁.

Следует вывод, что по проекции точки нельзя судить однозначно о её положении в пространстве.

Чтобы устранить эту неопределенность, т.е. сделать чертеж обратимым, введём еще одну плоскость проекций (π₂) и ещё один центр проецирования (S₂) (Рисунок 1.2).

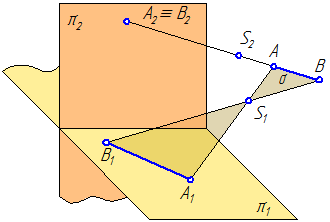
Рисунок 1.2 – Иллюстрация 1-го и 2-го свойств

Построим проекции точки А на плоскости проекций π₂. Из всех точек пространства только точка А имеет своими проекциями А₁ на плоскость π₁ и А₂ на π₂ одновременно. Все другие точки лежащие на проецирующих лучах будут иметь хотя бы одну отличную проекцию от проекций точки А (например, точка В).

Свойство 2. Проекция прямой есть прямая.

Докажем данное свойство.

Соединим точки А и В между собой (Рисунок 1.2). Получим отрезок АВ, задающий прямую. Треугольник ΔSAB задает плоскость, обозначенную через σ. Известно, что две плоскости пересекаются по прямой: σ∩π₁=А₁В₁, где А₁В₁ – центральная проекция прямой, заданной отрезком АВ.

Метод центрального проецирования – это модель восприятия изображения глазом, применяется главным образом при выполнении перспективных изображений строительных объектов, интерьеров, а также в кинотехнике и оптике. Метод центрального проецирования не решает основной задачи, стоящей перед инженером – точно отразить форму, размеры предмета, соотношение размеров различных элементов.

3.9. Задачи для самостоятельного решения

1. Задана плоскость  α = m//n (Рисунок 3.24). Известно, что K∈α.

Постройте фронтальную проекцию точки К.

Рисунок 3.24

2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).

Рисунок 3.25

3. Постройте проекции квадрата, принадлежащего плоскости α⊥π₂, если его диагональ MN //π₂ (Рисунок 3.26).

Рисунок 3.26

4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).

Рисунок 3.27

5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.

Рисунок 3.28

6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π₁.

7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π₁.

Плоскости, перпендикулярные одной плоскости проекций

Горизонтально-проецирующей называют плоскость, перпендикулярную плоскости (рис.29). Фронтальный и профильный следы такой плоскости будут параллельны оси .

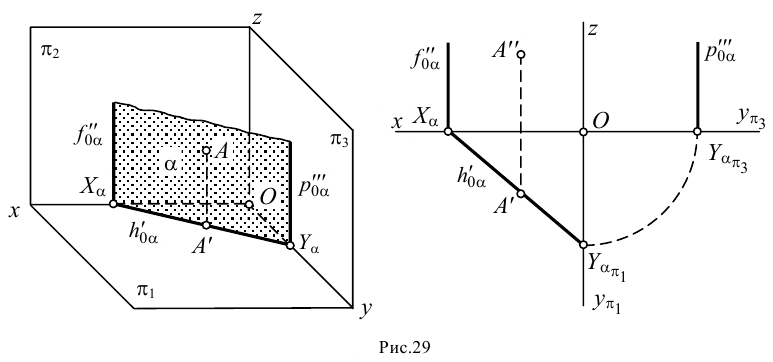
Фронтально-проецирующей называют плоскость, перпендикулярную плоскости  (рис.30). Горизонтальный и профильный следы фронтально-проецирующей плоскости будут параллельны оси .

Фронтальная проекция любой точки, лежащей в этой плоскости (например, точки ), всегда расположена на фронтальном следе плоскости.

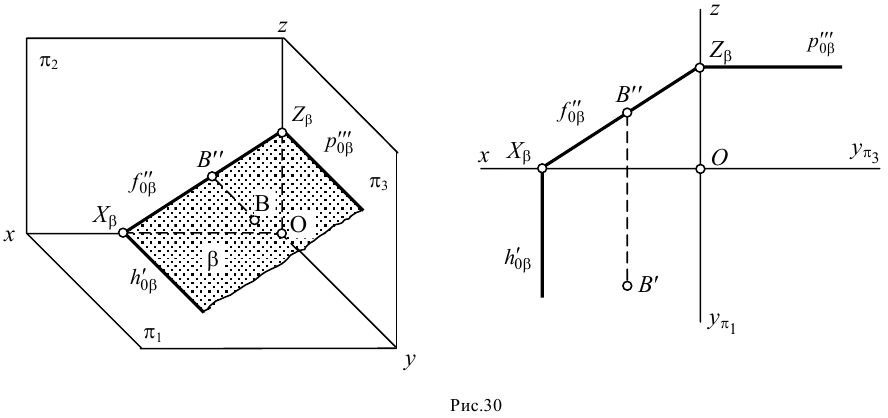
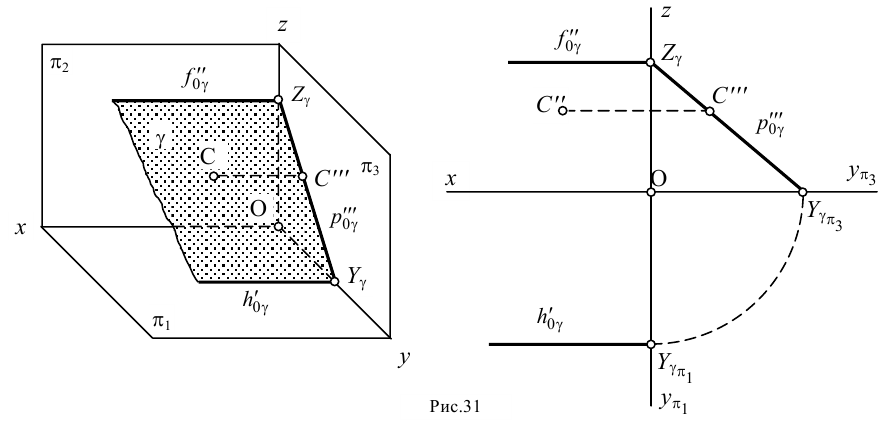
Профильно-проецирующей называют плоскость, перпендикулярную плоскости (рис.31). У такой плоскости фронтальный и горизонтальный следы будут параллельны оси .

Профильная проекция любой точки, лежащей в этой плоскости (например, точки ), всегда расположена на профильном следе плоскости.

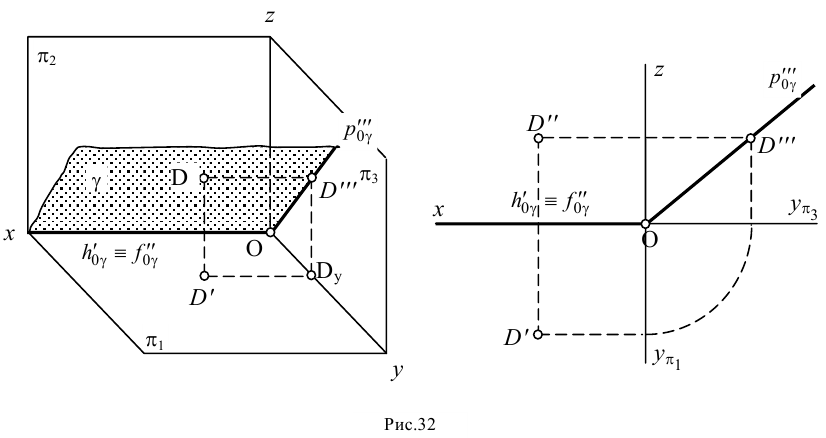
Осевой называют плоскость, проходящую через ось проекций. Осевая плоскость будет всегда перпендикулярна одной из плоскостей проекций, поэтому ее можно рассматривать как частный случай горизонтально-, фронтально- или профильно-проецирующей плоскости. У осевой плоскости два следа совпадают с одной из осей проекций (на рис.32 — с осью ).

Для однозначного определения положения осевой плоскости необходимо знать положение всех трех ее следов или двух сливающихся следов и еще хотя бы одной точки, лежащей в этой плоскости.

Взаимное положение прямой и плоскости

Прямая может занимать относительно плоскости следующие положения:

1. лежать в плоскости;
2. быть параллельной плоскости;
3. пересекать плоскость (частный случай пересечения — прямая может быть перпендикулярна плоскости).

Прямая лежит в плоскости, если проходит через две точки, принадлежащие этой плоскости.

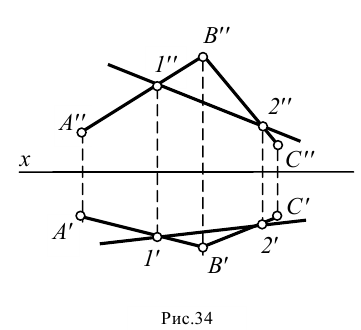
Пусть плоскость задана двумя пересекающимися прямыми и . Проводим в этой плоскости произвольную прямую . Для этого выбираем некоторую точку на прямой и точку на прямой и проводим прямую с проекциями и (рис.34). Эта прямая лежит в заданной плоскости, так как проходит через две точки (точки и ), лежащие в заданной плоскости.

Рассмотрим вариант, когда плоскость задана следами: прямая лежит в плоскости, если следы прямой лежат на одноименных следах плоскости (рис.35). Это же правило можно сформулировать и иначе: плоскость проходит через прямую, если ее следы проходят через одноименные следы прямой.

Если некоторая плоскость задана двумя пересекающимися прямыми, то для построения следов такой плоскости достаточно найти следы этих прямых и одноименные следы соединить прямыми линиями — эти прямые и будут искомыми следами плоскости. Аналогично могут быть построены следы плоскости, заданной двумя параллельными прямыми.

Поскольку случаи задания плоскости тремя точками, не лежащими на одной прямой, и прямой и точкой вне этой прямой всегда могут быть сведены к случаю задания плоскости двумя прямыми, то можно сказать, что для построения следов плоскости, заданной любым известным способом, необходимо построить следы двух любых прямых этой плоскости и через одноименные следы прямых провести искомые следы плоскости.

Пример 5. Построить три следа плоскости , заданной двумя пересекающимися прямыми  и (рис.36).

1. Строим проекции горизонтальных следов прямых и (рис.37): . Фронтальные проекции горизонтальных следов лежат на пересечении фронтальных проекций прямых с осью :

Горизонтальные проекции горизонтальных следов лежат на пересечении линий проекционной связи, проведенных из точек и , с соответствующей горизонтальной проекцией прямой:

2. Строим проекции фронтальных следов прямых и : . Горизонтальные проекции фронтальных следов лежат в точке пересечения горизонтальных проекций прямых с осью :

Фронтальные проекции фронтальных следов лежат на пересечении фронтальных проекций прямых с линиями проекционной связи, проведенными из точек  и :

3.    Через одноименные проекции следов проводим соответствующие следы плоскости (рис.38). Горизонтальный след плоскости проводим через горизонтальные проекции горизонтальных следов и . Фронтальный след  проводим через фронтальные проекции фронтальных следов и .

4.    В пересечении горизонтального  и фронтального следов  с осью отмечаем точку схода следов и проверяем правильность построений: .

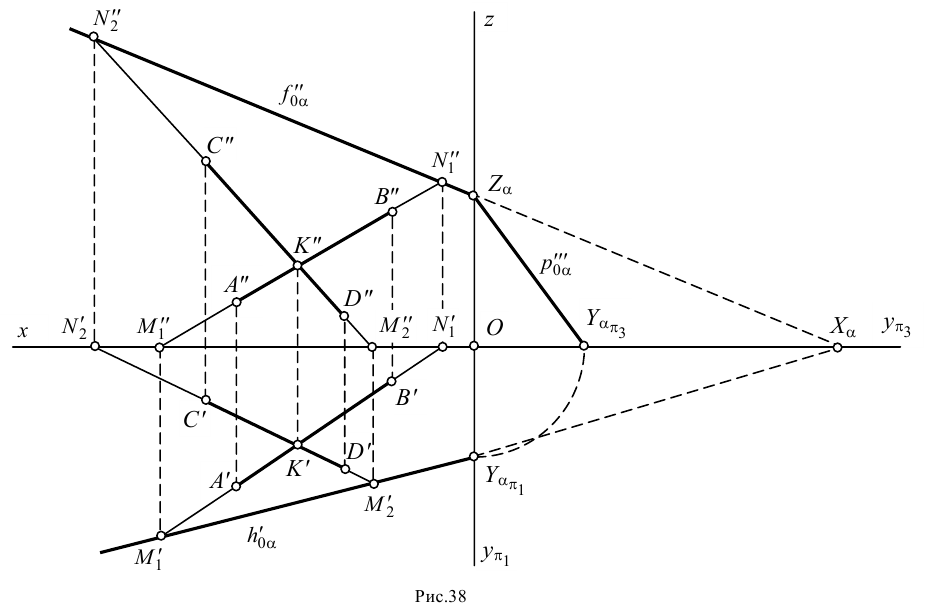
5.    В пересечении горизонтального  и фронтального  следов с осями проекций и отмечаем точки схода следов соответственно и .

6.    Точку схода следов с оси переносим на соответствующее по знаку направление оси , где отмечаем точку . Через точки схода следов и строим профильный след .

Заказать чертежи

СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ НА ЭПЮРЕ

Положение плоскости в пространстве определяется тремя ее точками, не лежащими на одной прямой. Поэтому чтобы задать на эпюре плоскость, достаточно задать три ее точки (рис. 206). Плоскость можно задать точкой и прямой (рис. 207, а), двумя параллельными прямыми (рис. 207, б), двумя пересекающимися прямыми (рис. 207, в), треугольником (рис. 207, г).

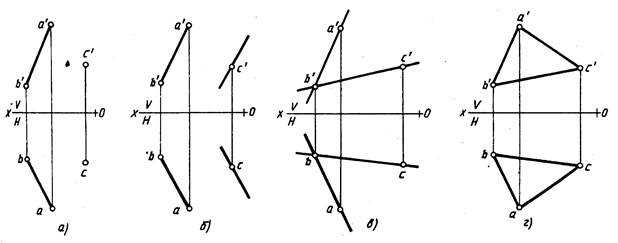
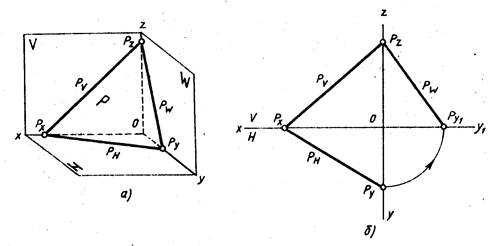
Можно задать плоскость следами. Следом плоскости называют прямую, по которой данная плоскость пересекает плоскость проекций. На рис. 208 Pv — фронтальный след плоскости Р, Рн — горизонтальный след плоскости Р, Pw — профильный след плоскости Р.

Различные случаи расположения плоскостей относительно плоскостей проекций

Плоскость общего положения — плоскость, расположенная наклонно ко всем плоскостям проекций (рис. 208). Такая плоскость пересекается с тремя плоскостями проекций по прямым, которые являются следами этой плоскости. Каждая пара следов сходится в точке, которая называется точкой схода следов плоскости и располагается на оси проекций. Плоскость общего положения имеет три точки схода, которые обозначаются Рх, Ру, Рz. В этих точках плоскость пересекает оси координат. Плоские фигуры, лежащие в плоскости общего положения, проецируются проекций с искажением.

Проецирующая плоскость — плоскость, перпендикулярная какой-либо плоскости проекций.

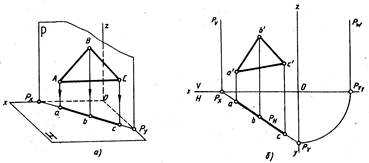
Горизонтально — проецирующая плоскость — плоскость, перпендикулярная горизонтальной плоскости проекций Н (рис. 209).

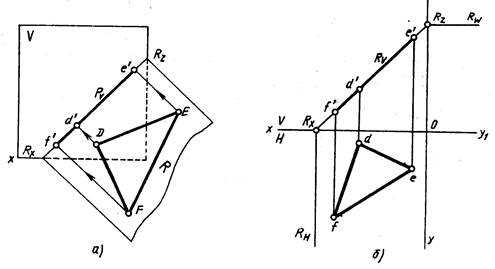
Фронтально — проецирующая плоскость — плоскость, перпендикулярная фронтальной плоскости проекции (рис. 210).

Профильно-проецирующая плоскость — плоскость, перпендикулярная профильной плоскости проекций (рис. 211).

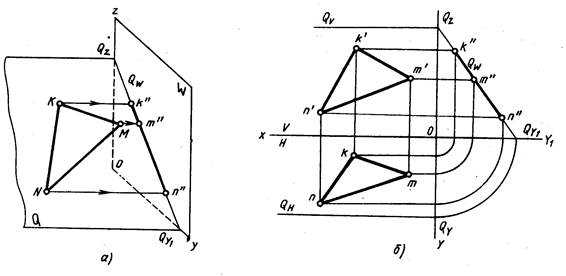
Проецирующая плоскость проецируется на плоскость проекций, к которой она перпендикулярна, в прямую. Па рис. 209 плоскость Р горизонтально-проецирующая, ΔАВС, лежащий в плоскости Р, проецируется в отрезок прямой линии, который совпадает со следом плоскости Рн. На рис. 210 ΔDEF, принадлежащий фронтально-проецирующей плоскости R, проецируется в отрезок, совпадающий со следом плоскости Rv. На рис. 211 ΔKMN, лежащий в профильно-проецирующей плоскости Q, проецируется на плоскость W в отрезок, совпадающий со следом плоскости Qw. Поэтому проецирующие плоскости часто используются в качестве вспомогательных при различных построениях. Например, чтобы через прямую AB провести горизонтально-проецирующую плоскость (рис. 212), достаточно через горизонтальную проекцию прямой ab провести горизонтальный след этой плоскости, так как все, что в этой плоскости лежит, в том числе и прямая AB, проецируется на ее горизонтальный след. Фронтальный след фронтально-проецирующей плоскости совпадает с фронтальной проекцией прямой a’b’ (рис. 213). Следы проецирующих плоскостей на других плоскостях проекций перпендикулярны соответствующим осям проекций (см. рис. 209, 210, 211).

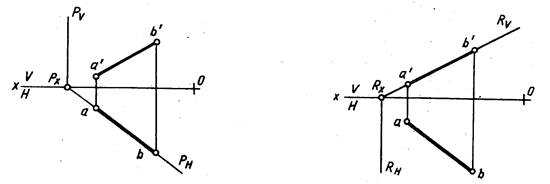
Рис. 212 Рис. 213

Плоскости, перпендикулярные двум плоскостям проекций, параллельны третьей плоскости проекций. Геометрические фигуры, лежащие в этих плоскостях, проецируются без искажения на ту плоскость проекций, которой параллельна данная плоскость (рис. 214, 215; 216). Называются такие плоскости так же, как и плоскость проекций, параллельно которой они расположены: горизонтальная плоскость (рис. 214), фронтальная плоскость (рис. 215), профильная плоскость (рис. 216).

Источник