Вектор напряженности магнитного поля

Магнитные линии и магнитный поток

Следующие значения найдены экспериментально вокруг магнита. магнитные силовые линии. Эти магнитные линии создают так называемое магнитное поле .

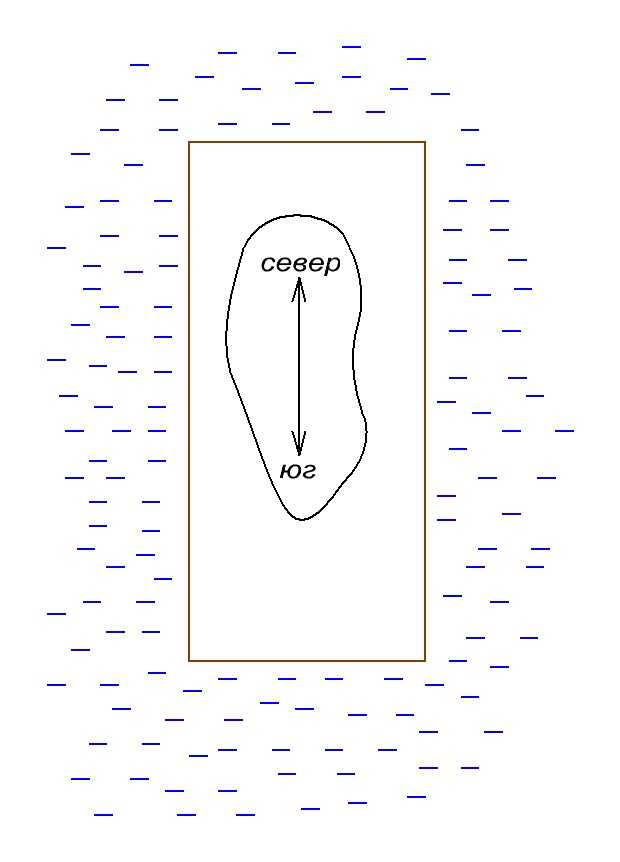
Как видно из рисунка, концентрация магнитных силовых линий по краям магнита гораздо выше, чем в центре магнита. Это показывает, что что магнитное Поле наиболее сильно именно по краям магнита, а в центре магнита оно практически равно нулю. Направление магнитных Направление линий поля — с севера на юг.

Ошибочно считать, что магнитные Силовые линии начинаются на северном полюсе и заканчиваются на южном. Это не так. Магнитные линии — они замкнуты и непрерывны. В магните это будет выглядеть следующим образом так.

При сближении двух противоположных полюсов возникает магнитное притяжение

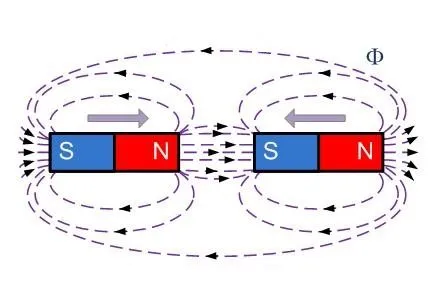
При сближении с одноименными полюсами они отталкиваются друг от друга.

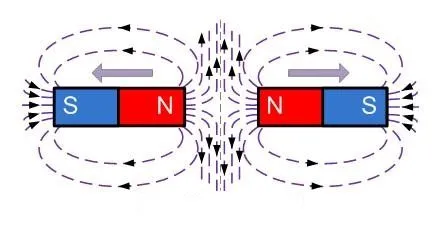
Итак, Важны следующие свойства магнитных силовых линий.

• Магнитные линии не поддаются гравитации.
• Никогда не пересекаются между собой.
• Всегда образуют замкнутые петли.
• Имеют определенное направление с севера на юг.
• Чем больше концентрация силовых линий, тем сильнее магнитное поле.
• Слабая концентрация силовых линий указывает на слабое магнитное поле.

Магнитные силовые линии, которые образуются магнитное поле, называют также магнитным потоком .

Итак, Давайте посмотрим на два рисунка и ответим на вопрос, где находится плотность потока магнитного плотность потока выше? На рисунке «a» или на рисунке «b»?

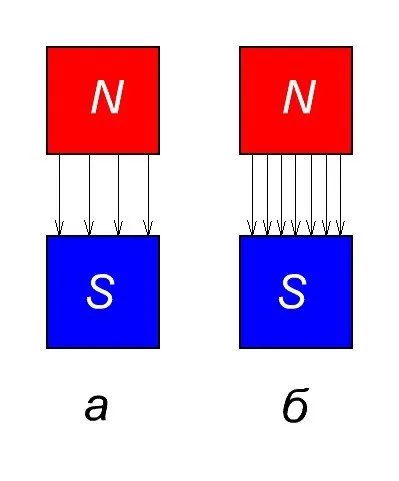
На рисунке «а» мы видим, что здесь всего несколько линий электропередач. магнитных а на рисунке «b» их концентрация значительно выше. Из этого можно сделать вывод, что плотность потока магнитного потока на рисунке «b» выше, чем на рисунке «a».

В физике формула магнитного поток записывается следующим образом

Ф – магнитный поток, Вебер

В – плотность магнитного потока, Тесла

a — угол между перпендикуляром n (обычно называемым нормалью) и плоскостью S, в градусах.

S — это плоскость, через которую магнитный поток, м2

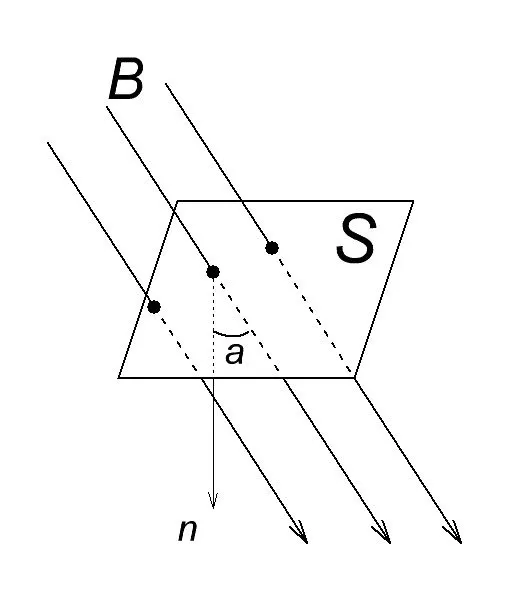
Что же такое 1 Вебер; А Вебер это магнитный Поток, создаваемый полем индукции 1 Тесла на площади 1 м2 перпендикулярно направлению магнитного поля.

Основные уравнения для вектора напряженности

Из определения вектора $\overrightarrow{H}$ и уравнения (4), следует весьма удобное уравнение для вычисления поля в магнетиках:

Закон полного тока при наличии магнетиков имеет вид:

Формула (7) выражает теорему о циркуляции вектора напряженности магнитного поля, которая гласит:

Теорема

«Циркуляция вектора напряженности магнитного поля по некоторому контуру равна алгебраической сумме макроскопических токов, которые охвачены заданным контуром».

В вакууме $\overrightarrow{J\ }=0$, тогда:

\

Напряженность поля прямолинейного бесконечного проводника в вакууме определяется формулой:

\

где $b$ — расстояние от проводника до точки, где рассматривается поле. Из формулы (9) определяется размерность напряженности магнитного поля. Основная единица напряженности в системе СИ — ампер деленный на метр ($\frac{А}{м}$).

Связь и вектора напряженности магнитного поля с намагниченностью и вектором магнитной индукции

Обычно вектор намагниченности ($\overrightarrow{J}$) связывают с вектором напряженности в каждой точке магнетика:

где $\varkappa $ — магнитная восприимчивость, безразмерная величина. Для неферромагнитных веществ и в не больших полях $\varkappa $ не зависит от напряженности. В анизотропных средах $\varkappa $ является тензором и направления $\overrightarrow{J}$ и $\overrightarrow{H}$ не совпадают.

Помимо магнитной восприимчивости в магнетиках используют другую безразмерную физическую величину, которая характеризует магнитные свойства вещества — это относительная магнитная проницаемость (или просто магнитная проницаемость ($\mu $)) вещества. Причем:

Тогда между индукцией магнитного поля в магнетике и напряженностью магнитного поля существует следующая связь:

Формула (12) показывает, что в изотропных средах векторы $\overrightarrow{B}$ и $\overrightarrow{H}$ имею одинаковое направление, однако по модулю напряженность поля в $\mu {\mu }_0$ раз меньше.

Опыт Эрстеда

Довольно продолжительное время электрические и магнитные поля изучались раздельно. Их взаимосвязь была обнаружена совершенно случайно. Существует легенда, что Кристиан Эрстед показывал ученикам на своей лекции в университете влияние толщины проводника на силу тока. При этом на демонстрационном столе лежал компас, оставшийся от предыдущей лекции

Во время рассказа Эрстеда о природе нагрева проволоки, один из его студентов обратил внимание, что стрелка компаса изменила положение. Этот эффект после позволил учёному утверждать, что на магнитную стрелку, расположенную вблизи с проводником тока, действуют силы, стремящие её развернуть. Проведя ряд опытов, учёный установил, что на направление указателя влияла полярность подключения источника питания

При её изменении стрелка сразу же изменяла своё направление на противоположное. Но оказалось, что влияние магнитного потока настолько мало, что обнаружить его, возможно, только с помощью чувствительных приборов

Проведя ряд опытов, учёный установил, что на направление указателя влияла полярность подключения источника питания. При её изменении стрелка сразу же изменяла своё направление на противоположное. Но оказалось, что влияние магнитного потока настолько мало, что обнаружить его, возможно, только с помощью чувствительных приборов.

Чтобы более точно представить, по какому принципу происходит поворот магнитной стрелки вблизи проводника с током нужно рассмотреть проволоку с торца. Тогда можно будет изучить два случая:

• ток идёт от наблюдающего;
• заряды двигаются к исследователю.

Если установить множество стрелок вокруг проводника, то окажется, что после пропускания тока они выстроятся так, что образуют своеобразную окружность. При этом их полюса будут противоположны друг другу. Эти стрелки примут положение по касательной к магнитным линиям. Таким образом, можно будет увидеть, что линии, описывающие распространение поля, представляют окружность. Их же направления в первом случае будут по часовой стрелке, а во втором — против.

Это важное свойство магнитных линий и наблюдал Эрстед. Ампер же смог развить исследование дальше. Он установил, что если взять два проводника, разместить их параллельно и пустить по ним токи в одном направлении, то возникает сила притягивания

Если же в одном из них поменять подключение — проводники начинают отталкиваться. Именно благодаря Амперу удалось эмпирически доказать, как происходит взаимодействие проводника, по которому течёт ток, с полем постоянного магнита и описать зависимость зарядов от их направления

Он установил, что если взять два проводника, разместить их параллельно и пустить по ним токи в одном направлении, то возникает сила притягивания. Если же в одном из них поменять подключение — проводники начинают отталкиваться. Именно благодаря Амперу удалось эмпирически доказать, как происходит взаимодействие проводника, по которому течёт ток, с полем постоянного магнита и описать зависимость зарядов от их направления.

Циркуляция вектора напряженности магнитного поля

Существует теорема о циркуляции. магнитного поля. Это одна из фундаментальных теорем электродинамики, сформулированная Анри Ампером. Ее также Иногда его называют теоремой или законом Ампера. Теорема о циркуляции магнитного поля — Своего рода аналогия с теоремой Гаусса о циркуляции вектора. напряженности электрического поля.

Теорема о циркуляции магнитного поля

Циркуляция вектора напряженности магнитного поля в замкнутой цепи равен алгебраической сумме линейных токов в цепи, в которой рассматривается циркуляция.

Определите циркуляцию вектора напряженности для замкнутого контура L .

I 1 = 5 A, I 2 = 2 A, I 3 = 10 A, I 4 = 1 A .

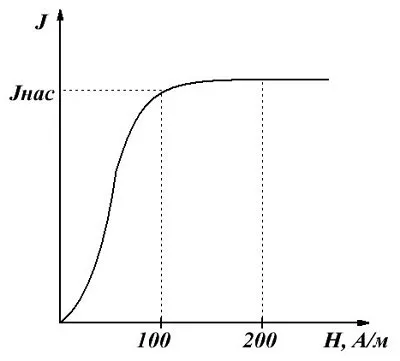
Теорема о циркуляции утверждает, что

Рассматриваемый контур состоит из потоков I 1, I 2, I 3 .

Подставим значения, указанные на рисунке, для направлений потоков и рассчитаем трафик:

∮ H → d r → = ∑ I m = 5 A 12 A + 10 A = 13 A .

Магнитное поле — это вихревое поле, которое не является динамическим. Вектор циркуляции напряженности как правило, не равна нулю.

Природа магнетизма

Согласно одной из легенд, когда-то давным-давно жил в Греции пастух по имени Магнес. И вот шел он как-то со своим стадом овец, присел на камень и обнаружил, что конец его посоха, сделанный из железа, стал притягиваться к этому камню. С тех пор стали называть этот камень магнетит в честь Магнеса. Этот камень представляет из себя оксид железа.

Если такой камень положить на деревянную доску на воду или подвесить на нитке, то он всегда выстраивался в определенном положении. Один его конец всегда показывал на СЕВЕР, а другой  — на ЮГ.

Этим свойством камня пользовались древние цивилизации. Поэтому, это был своего рода первый компас. Потом уже стали обтачивать такой камень и делать из разные фигурки. Например, так выглядел китайский древний компас, ложка которого была сделана из того самого магнетита. Ручка у этой ложки всегда показывала на ЮГ.

Ну а далее дело шло за практичностью и маленькими габаритами. Из магнетита вытачивали маленькие стрелки, которые подвешивали на тонкую иглу посередине. Так стали появляться первые малогабаритные компасы.

Древние цивилизации, конечно, не знали еще что такое север и юг. Поэтому, одну сторону магнетита они назвали северным полюсом (North), а противоположный конец — южным (South). Названия на английском очень легко запомнить, если кто смотрел американский мультфильм «Южный парк», он же Сауз (South) парк).

Напряженность магнитного поля

Напряженность магнитного поля является вспомогательной величиной, помогающей в математическом описании магнитного поля.

Вектор напряженности магнитного поля (H ⃗) можно рассматривать как комбинацию принципиально разных физических величин, часть из них относится к полю (слагаемое, содержащее вектор магнитной индукции), часть к веществу, и, следовательно, напряженность магнитного поля физическим смыслом не обладает:

$\vec{H}=\frac{\vec{B}}{\mu_{0}}-\vec{P}_{m}\left( 8 \right)$,

где $\vec{P}_{m}$ – вектор намагниченности (вектор интенсивности намагничения вещества). Однако вектор напряженности является количественной характеристикой магнитного поля, которая не зависит от магнитных свойств вещества, в котором его рассматривают. Применение $\vec{H}$ упрощает количественные описания магнитного поля в веществе.

В однородном магнитном веществе напряженность магнитного поля определим как:

$\vec{H}=\frac{\vec{B}}{\mu \mu_{0}}\left( 9 \right)$.

Важность данной физической величины заключается в том, что она не зависит от магнитных свойств вещества, в котором локализовано магнитное поле (в отличии от $\vec{B}$). Напряженность магнитного поля определяют:

Напряженность магнитного поля определяют:

• сила тока, создающая магнитное поле;
• геометрия объекта, по которому следует электрический ток (форма тела);
• расположение точки, в которой рассматривается поле относительно источник поля.

Для однородной магнитной среды направления векторов магнитной индукции и напряженности магнитного поля совпадают.

Напряжённость магнитного поля для постоянных токов разной конфигурации можно рассчитать, применяя закон Био-Савара-Лапласа:

$dH=\frac{Idl\sin \propto }{4\pi r^{2}}\left( 10 \right)$, где:

• $Idl$ – элемент тока на проводнике, который создает магнитное поле;
• $\vec{r}$ – радиус – вектор, который провели от элемента тока в точку, в которой исследуем поле;
• $\propto =\hat{d\vec{l}\vec{r}}$ — угол между соответсвующим вектором и направлением течения тока;
• $dH$ – величина элементарного магнитного поля, которое в рассматриваемой точке создает элемент тока.

Уравнение (10) можно записать в векторной форме:

$d\vec{H}=\frac{I}{4\pi r^{3}}\left\left(11\right)$.

В соответствии с правилами векторных произведений мы получаем, что $d\vec{H}$ нормален плоскости, в которой находятся векторы $d\vec{l}$ и $\vec{r}$.

Вектор напряженности магнитного поля подчиняется принципу суперпозиции, поэтому напряженность магнитного поля, которое создает весь проводник с постоянным током, в рассматриваемой точке равна:

$\vec{H}=\frac{I}{4\pi }\int \frac{\left}{r^{3}}\left( 12 \right)$.

Закон (11) бы эмпирически получен учеными Ж.Б. Био и Ф. Саваром при исследованиях действия электрических токов на магнитную стрелку. П.С. Лаплас провел анализ результатов экспериментов Био и Савара понял, что напряженность магнитного поля тока является суммой напряженностей полей, которые создают отдельные токи.

Как связана индукция и напряженность магнитного поля?

Магнит — это вещество, которое находится под воздействием магнитного поля (или, как это называют физики, приобретает магнитную силу). магнитный Почти все вещества являются магнитами. Намагниченность веществ обусловлена тем, что вещества имеют свои собственные микроскопические магнитные поля, магнитные поля, которые генерируются электронами на их орбитах. Если нет внешнего магнитное поле отсутствует, микроскопическое поля расположены беспорядочно, но когда они подвергаются воздействию внешней силы магнитного поля они правильно выровнены.

Чтобы охарактеризовать намагниченность различных веществ, мы используем так называемый вектором намагниченности J .

Под влиянием внешних магнитного поля с магнитной индукции B0, магнетит становится намагниченным и производит магнитное поле с магнитной с индукцией B’. Следовательно, полная индукция B состоит из двух членов

Здесь возникает проблема вычисления магнитной индукции намагниченного вещества B’, и для решения этой задачи необходимо подсчитать электронные микротоки всего вещества, что практически нереально.

Альтернативой этому решению является введение вспомогательных параметров, т.е. напряженность магнитного поля Н и магнитная Чувствительность x. Чувствительность связана с магнитную индукции B и намагниченности вещества J с помощью следующего выражения.

где В – магнитная индукция,

μ0 – магнитная постоянная, μ0 = 4π*10-7 Гн/м.

В то же время вектор намагниченности J, связанный с с напряженность магнитного поля B параметр, характеризующий магнитные свойства материи и выражается как магнитной восприимчивостью χ

где J — вектор намагниченности вещества,

μr – относительная магнитная проницаемость вещества.

Однако наиболее распространенным типом характеристики является магнитных свойства веществ, относительные магнитную проницаемость μr.

Таким образом, отношения между напряженностью и магнитной индукция имеет следующий вид

где μ0 – магнитная Постоянная, μ0 = 4π*10-7 Гн/м,

μr – относительная магнитная проницаемость вещества.

Поскольку намагниченность вакуума равна нулю (J = 0), то напряженность магнитного поля в вакууме она равна

Из этого можно вывести следующее выражение напряженности для магнитного поля, которую дает прямой провод с током в

где I — ток, протекающий через провод,

b — расстояние от центра провода до точки, где напряженность магнитного поля.

Как видно из этого выражения, единица измерения напряженности амперы на метр (А/м) или перв.д (Е)

Таким образом, магнитная индукция В и напряженность H обозначает основной магнитного поля, а магнитная проницаемость μ r – магнитной характеристика вещества.

Вектор напряжённости магнитного поля как вспомогательный вектор для описания поля в магнетиках

Когда мы рассматриваем магнитное поле в вакууме при отсутствии магнетиков, магнитное поле порождается токами проводимости и выполняется равенство:

где $\overrightarrow{j}$ — вектор плотности токов проводимости.

В магнетиках поле возникает благодаря токам проводимости и молекулярным токам ($\overrightarrow{j_m}$), что необходимо учитывать. Для молекулярных токов имеет место векторное равенство:

где $\overrightarrow{j_m}$ — объемная плотность молекулярных токов, $\overrightarrow{J\ }$ — вектор намагниченности. Так, при наличии магнетиков выражение (1) с учетом равенства (2) примет вид:

Выразим ток проводимости из уравнения (3), получим:

Циркуляция вектора напряженности магнитного поля

Существует теорема о циркуляции магнитного поля. Это одна из основных теорем электродинамики, сформулированная Анри Ампером. Ее также иногда называют теоремой или законом Ампера. Теорема о циркуляции магнитного поля — своеобразный аналог теоремы Гаусса о циркуляции вектора напряженности электрического поля.

Теорема о циркуляции магнитного поля

Циркуляция вектора напряженности магнитного поля по замкнутому контуру равна алгебраической сумме токов проводимости, охваченных контуром, по которому рассматривается циркуляция.

Определить циркуляцию вектора напряженности для замкнутого контура L .

I 1 = 5 A , I 2 = 2 A , I 3 = 10 A , I 4 = 1 A .

По теореме о циркуляции:

Рассматриваемый контур охватывает токи I 1 , I 2 , I 3 .

Подставим значения c учетом указанных на рисунке направлений токов и вычислим циркуляцию:

​​​​​ ∮ H → d r → = ∑ I m = 5 A 12 A + 10 A = 13 A .

Магнитное поле — вихревое поле, которое не является потенциальным. Циркуляция вектора напряженности в общем случае отлична от нуля.

Магнитное поле проводника с током

Электрический ток, протекающий по проводнику с током, создает в окружающем его пространстве магнитное поле. Чем больше ток, проходящий по проводнику, тем сильнее возникающее вокруг него магнитное поле.

Магнитные силовые линии этого поля располагаются по концентрическим окружностям, в центре которых находится проводник с током.

Направление линий магнитного поля вокруг проводника с током всегда находится в строгом соответствии с направлением тока, проходящего по проводнику.

Направление магнитных силовых линий можно определить по правилу буравчика: если поступательное движение буравчика (1) совпадает с направлением тока (2) в проводнике, то вращение его рукоятки укажет направление силовых линий (4) магнитного поля вокруг проводника.

При изменении направления тока линии магнитного поля также изменяют свое направление.

По мере удаления от проводника магнитные силовые линии располагаются реже. Следовательно, индукция магнитного поля уменьшается.

Направление тока в проводнике принято изображать точкой, если ток идет к нам, и крестиком, если ток направлен от нас.

Для получения сильных магнитных полей при небольших токах обычно увеличивают число проводников с током и выполняют их в виде ряда витков; такое устройство называют катушкой.

В проводнике, согнутом в виде витка, магнитные поля, образованные всеми участками этого проводника, будут внутри витка иметь одинаковое направление. Поэтому интенсивность магнитного поля внутри витка будет больше, чем вокруг прямолинейного проводника. При объединении витков в катушку магнитные поля, созданные отдельными витками, складываются. При этом концентрация силовых линий внутри катушки возрастает, т. е. магнитное поле внутри нее усиливается.

Чем больше ток, проходящий через катушку, и чем больше в ней витков, тем сильнее создаваемое катушкой магнитное поле. Магнитное поле снаружи катушки также складывается из магнитных полей отдельных витков, однако магнитные силовые линии располагаются не так густо, вследствие чего интенсивность магнитного поля там не столь велика, как внутри катушки.

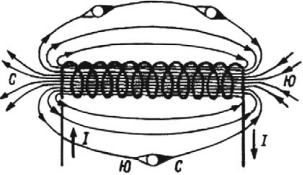
Магнитное поле катушки с током имеет такую же форму, как и поле прямолинейного постоянного магнита: силовые магнитные линии выходят из одного конца катушки и входят в другой ее конец. Поэтому катушка с током представляет собой искусственный электрический магнит. Обычно для усиления магнитного поля внутрь катушки вставляют стальной сердечник; такую катушку называют электромагнитом.

Направление линий магнитной индукции катушки с током находят по правилу правой руки:

если мысленно обхватить катушку с током ладонью правой руки так, чтобы четыре пальца указывали направление тока в ее витках, тогда большой палец укажет направление вектора магнитной индукции.

Для определения направления линий магнитного поля, создаваемого витком или катушкой, можно использовать также правило буравчика:

если вращать ручку буравчика по направлению тока в витке или катушке, то поступательное движение буравчика укажет направление вектора магнитной индукции.

Электромагниты нашли чрезвычайно широкое применение в технике. Полярность электромагнита (направление магнитного поля) можно определить и с помощью правила правой руки.

Закон полного тока

В некоторых случаях для нахождения напряженности магнитного поля вместо закона Био-Савара-Лапласа применяют закон полного тока, который формулируется в следующем виде:

$\oint {H_{l}dl=\sum {I_{m}\left( 13 \right),} }$

где $\oint {H_{l}dl} $ — циркуляция вектора напряженности по замкнутому контуру $l$, $\sum I_{m}$ — сумма токов (с учетом знака), которые охватывает контур $l$.

Рисунок 1. Контур. Автор24 — интернет-биржа студенческих работ

Так, если контур $l$ на рис.1 охватывает четыре тока, при этом токи $I_1$, $I_2,$ $I_3$ , больше нуля, $I_4$

$\oint {H_{l}dl} =I_{1}+I_{2}+I_{3}-I_{4}(14).$

Магнитное напряжение.

По аналогии с электрическим напряжением, понятие Ампер на метр ( A/m ) или Эрстед ( E ) H используется при расчете магнитных поля, концепция магнитного Магнитный потенциал между двумя точками a и b однородного тела — это напряжение U m. магнитного поля, на одной линии (рис. 2,a) выражается магнитным потенциалом между двумя точками a и b магнитной (рис. 2,а) выражается произведением напряженности поля и расстояние между этими точками: Если в однородном поле две точки a и b не лежат на одной прямой, но имеют расстояние L магнитной линии (рис. 2,b), сначала рассчитывается напряженность H, тогда продольный наклон вектора равен напряженности вдоль отрезка, т.е. HL = H cosa, где a — угол между векторами H и HL. Магнитный потенциалНеоднородный магнитном поле магнитное Напряжение между двумя точками a и b равно сумме элементарных напряжений HLdL в элементарных сегментах dL вдоль выбранного расстояния между этими точками (рис. 2, c):

Магнитное напряжение Um может зависеть от выбранного расстояния между начальной точкой и точкой назначения. Магнитный потенциал измеряется в амперах в системе СИ:

Магнитный потенциал вдоль любого замкнутого пути (контура) является МП вдоль этого контура. Таким образом, MF можно определить как сумму элементарных магнитных Напряжения HLdL по замкнутому пути: где знак обозначает суммирование (интегрирование) по замкнутому пути элементарных напряжений HLdL.

Вектор напряженности магнитного поля

Для описания магнитного поля Двумя наиболее важными характеристиками являются индуктивность B →. и напряженность H →. Эти величины связаны друг с другом. Рассмотрим, что такое напряженность магнитного поля, что это значит, каков физический смысл этой величины.

Напряженность магнитного поля — векторная физическая величина, в общем случае равная разности векторов индукции магнитного поля B → и намагниченность P m → .

Мощность обозначается буквой H →. Единица измерения напряженности магнитного поля в системе СИ — амперы на метр (Am p e r m e t r ).

Формула напряженности магнитного поля:

H → = 1 μ 0 B → — P m → .

Здесь коэффициент μ 0 — магнитная является константой. μ 0 = 1, 25663706 N A 2 .

Магнитное поле прямолинейного тока

Линии магнитной индукции представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику. Центр окружностей совпадает с осью проводника.

Если ток идет вверх, то силовые линии направлены против часовой стрелки. Если вниз, то они направлены по часовой стрелке. Их направление можно определить с помощью правила буравчика или правила правой руки:

Правило буравчика (правой руки)

Если большой палец правой руки, отклоненный на 90 градусов, направить в сторону тока в проводнике, то остальные 4 пальца покажут направление линий магнитной индукции.

Модуль вектора магнитной индукции на расстоянии r от оси проводника:

B = μ μ 0 I 2 π r . .

Магнитное поле кругового тока

Силовые линии представляют собой окружности, опоясывающие круговой ток. Вектор магнитной индукции в центре витка направлен вверх, если ток идет против часовой стрелки, и вниз, если по часовой стрелке.

Определить направление силовых линий магнитного поля витка с током можно также с помощью правила правой руки:

Если расположить четыре пальца правой руки по направлению тока в витке, то отклоненный на 90 градусов большой палец, покажет направление вектора магнитной индукции.

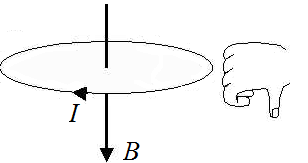
Модуль вектора магнитной индукции в центре витка, радиус которого равен R:

Модуль напряженности в центре витка:

Пример №2. На рисунке изображен проволочный виток, по которому течет электрический ток в направлении, указанном стрелкой. Виток расположен в вертикальной плоскости. Точка А находится на горизонтальной прямой, проходящей через центр витка. Как направлен (вверх, вниз, влево, вправо) вектор магнитной индукции магнитного поля в точке А?

Если мысленно обхватить виток так, чтобы четыре пальца правой руки были бы направлены в сторону тока, то отклоненный на 90 градусов большой палец правой руки показал бы, что вектор магнитной индукции в точке А направлен вправо.

Что такое однородное и неоднородное магнитное поле

Однородное магнитное поле — это магнитное поле, в любой точке которого сила действия на магнитную стрелку одинакова по модулю и направлению.

В однородном магнитном поле заряженная частица, движущаяся со скоростью \( \overrightarrow v\) перпендикулярно линиям индукции, подвергается воздействию силы \(\overrightarrow{F_л}\), постоянной по модулю и направленной перпендикулярно вектору скорости \(\overrightarrow v\). В таком поле магнитная индукция B во всех точках одинакова по модулю и направлению.

Благодаря силе Лоренца в однородном поле частицы движутся равномерно по окружности с центростремительным ускорением.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут. Сила Лоренца \(\overrightarrow{F_л}\) — электромагнитная сила со стороны магнитного поля, действующая на движущийся заряд q:

Сила Лоренца \(\overrightarrow{F_л}\) — электромагнитная сила со стороны магнитного поля, действующая на движущийся заряд q:

\(F=qE+q\left\)

Неизменность по модулю центростремительного ускорения частицы, движущейся с постоянной по модулю скоростью, означает, что частица равномерно движется по окружности с радиусом r.

Радиус r окружности определяется как частное произведения массы m со скоростью v и произведения электрического заряда q с индукцией B.

Радиус траектории движения частицы с постоянной массой и ее скорость не влияют на период ее обращения в однородном поле.

В однородном магнитном поле максимальный вращающий момент \(M_{max}\) при воздействии замкнутых проводников, изготовленных из очень тонкой проволоки разных размеров и форм, с током приобретает свойства:

1. Он пропорционален силе тока в контуре I.
2. Пропорционален площади контура.
3. Для контуров с одинаковой площадью не зависит от их формы.

Таким образом, максимальный вращающий момент становится пропорциональным магнитному моменту \(P_{m}\) контура с током:

\(P_m=I\ast S.\)

Величина магнитного момента \(P_{m}\) характеризует действие магнитного поля на плоский контур с током.

В данном случае значение вращающего момента \(M_{max}\), действующего на контур с магнитным моментом \(P_{m}\), принимают равным единице.

Следовательно, формула для определения индукции B в однородном магнитном поле приобретает вид:

\(B=\frac{M_{max}}{P_m}.\)

Примеры однородных магнитных полей:

1. Магнитное поле внутри соленоида. Соленоид — длинная цилиндрическая катушка, состоящая из нескольких витков плотно намотанной по винтовой лестнице проволоки. Каждый виток создает свое магнитное поле, которое складывается с другими в общее поле. Оно является однородным при условии, что длина катушки значительно превосходит ее диаметр. Тогда внутри соленоида линии поля будут параллельными его оси и прямыми.
2. Магнитное поле внутри тороидальной катушки. Здесь линии замыкаются внутри самой катушки. Представлены в виде окружностей, параллельных оси тора. Токи в обмотке тороидальной катушки текут равномерно по часовой стрелке.

Неоднородное магнитное поле — это магнитное поле, в котором сила, действующая на помещенную в это поле магнитную стрелку, в разных точках поля может быть различной как по модулю, так и по направлению.

В неоднородном магнитном поле магнитная индукция в разных местах имеет различные модули и направления. Для вычисления значения вектора \(\overrightarrow B\) в неоднородном поле необходимо определить вращающий момент, действующий на него. Для этого в некую точку помещают контур размеров, меньших в сравнении с расстояниями, на которых поле заметно меняется.

Примеры неоднородных магнитных полей:

1. Снаружи соленоида. Линии на концах катушки соленоида не являются параллельными друг другу и тянутся от одного конца к другому. А снаружи вблизи боковой поверхности катушки поле практически отсутствует.
2. Снаружи полосового магнита. Магнитное поле полосового магнита подобно полю вокруг соленоида. Магнитные линии тянутся от одного конца магнита к другому по направлению от северного полюса к южному. Имеется нейтральная зона.

Отличия однородного и неоднородного магнитных полей

1. Однородное поле находится внутри проводника или магнита, неоднородное — снаружи.
2. В однородном поле сила, действующая в разных точках, одинакова. В неоднородном — различна.
3. Линии однородного магнитного поля являются одинаковыми по густоте и параллельными друг другу. В неоднородном поле линии отличаются по густоте и искривлены.
4. Линии магнитной индукции однородного поля находятся на равном расстоянии друг от друга.

Вектор магнитной индукции

Вектор магнитной индукции — силовая характеристика магнитного поля. Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как → B . Единица измерения — Тесла (Тл).

За единицу магнитной индукции можно принять магнитную индукцию однородного поля, котором на участок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила, равна 1 Н. 1 Н/(А∙м) = 1 Тл.

Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины проводника:

B = F A m a x I l . .

За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.

Наглядную картину магнитного поля можно получить, если построить так называемые линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор магнитной индукции в данной точке поля.

Особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Поэтому магнитное поле — вихревое поле.

Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобным электрическим, в природе нет.