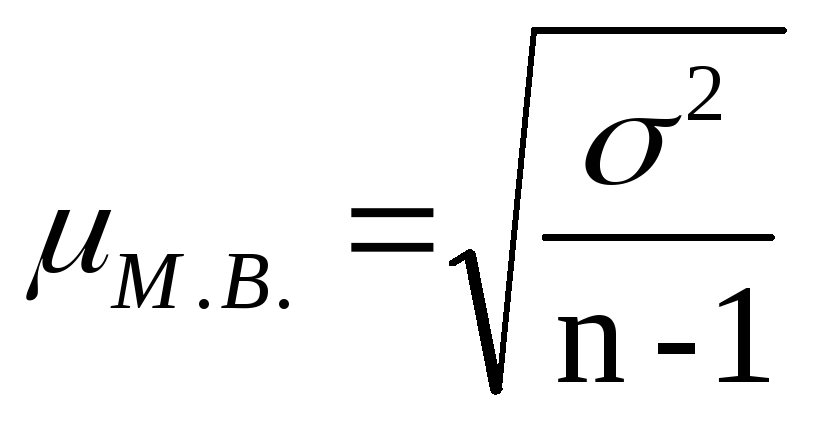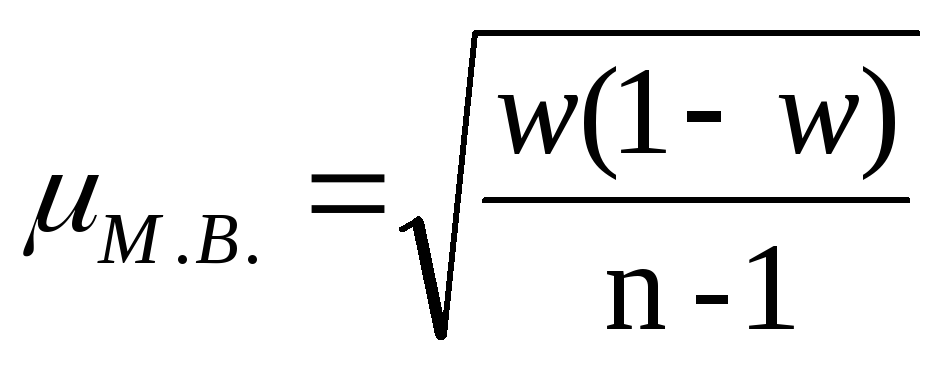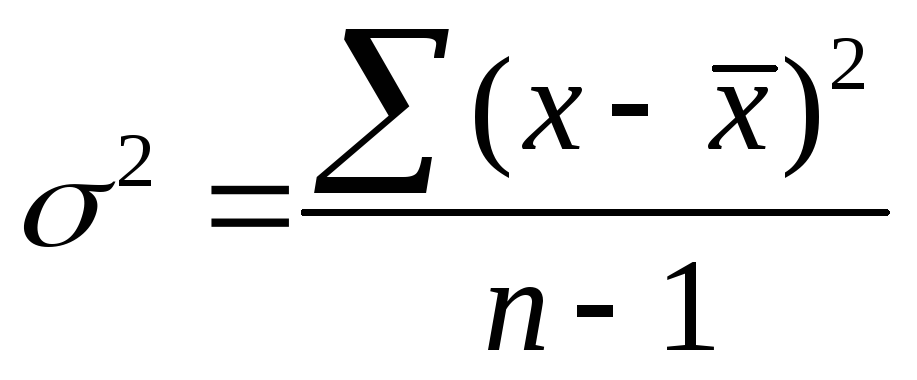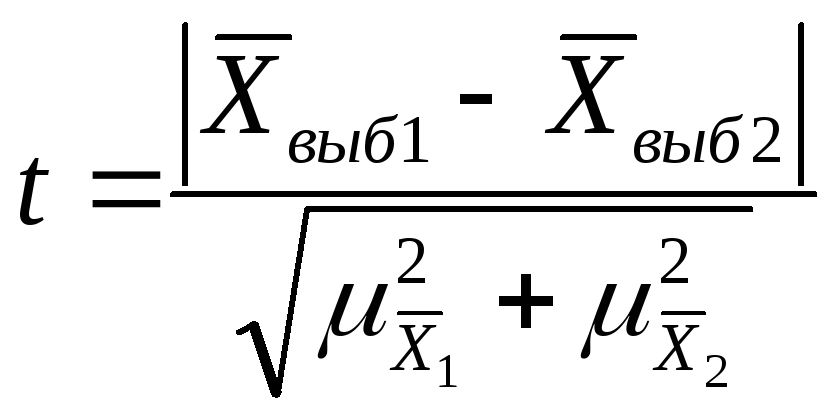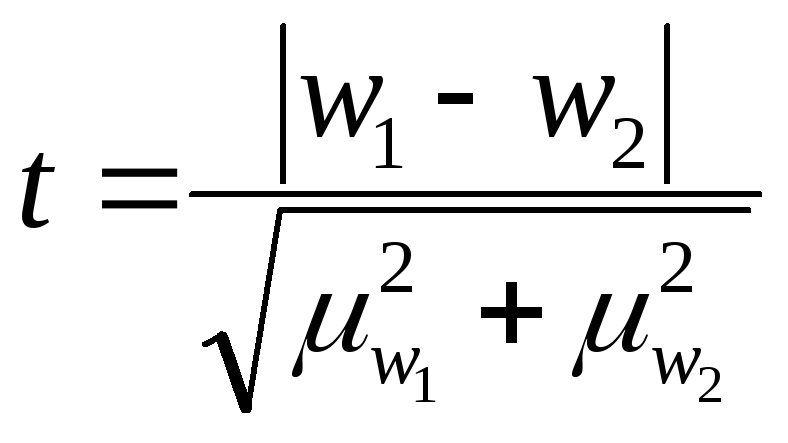Понимание ошибок выборки
Ошибка выборки — это отклонение значения выборки от истинного значения совокупности из-за того, что выборка не является репрезентативной для генеральной совокупности или каким-либо образом смещена. Даже рандомизированные выборки будут иметь некоторую ошибку выборки, поскольку это всего лишь приблизительная оценка генеральной совокупности, из которой она взята.
Ошибки выборки могут быть устранены при увеличении размера выборки, а также путем обеспечения того, чтобы выборка адекватно представляла всю генеральную совокупность. Предположим, например, что компания XYZ предоставляет услугу на основе подписки, которая позволяет потребителям вносить ежемесячную плату за потоковую передачу видео и других программ через Интернет.
Фирма хочет опросить домовладельцев, которые смотрят по крайней мере 10 часов программ в Интернете каждую неделю и платят за существующую службу потокового видео. XYZ хочет определить, какой процент населения заинтересован в более дешевой подписке. Если XYZ не продумает тщательно процесс выборки, могут возникнуть несколько типов ошибок выборки.
Типы выборок
Выборки делятся на два типа:
1. Вероятностные выборки 1.1 Случайная выборка (простой случайный отбор) Такая выборка предполагает однородность генеральной совокупности, одинаковую вероятность доступности всех элементов, наличие полного списка всех элементов. При отборе элементов, как правило, используется таблица случайных чисел. 1.2 Механическая (систематическая) выборка Разновидность случайной выборки, упорядоченная по какому-либо признаку (алфавитный порядок, номер телефона, дата рождения и т.д.). Первый элемент отбирается случайно, затем, с шагом ‘n’ отбирается каждый ‘k’-ый элемент. Размер генеральной совокупности, при этом – N=n*k 1.3 Стратифицированная (районированная) Применяется в случае неоднородности генеральной совокупности. Генеральная совокупность разбивается на группы (страты). В каждой страте отбор осуществляется случайным или механическим образом. 1.4 Серийная (гнездовая или кластерная) выборка При серийной выборке единицами отбора выступают не сами объекты, а группы (кластеры или гнёзда). Группы отбираются случайным образом. Объекты внутри групп обследуются сплошняком.
2.Невероятностные выборки Отбор в такой выборке осуществляется не по принципам случайности, а по субъективным критериям – доступности, типичности, равного представительства и т.д.. 2.1. Квотная выборка Изначально выделяется некоторое количество групп объектов (например, мужчины в возрасте 20-30 лет, 31-45 лет и 46-60 лет; лица с доходом до 30 тысяч рублей, с доходом от 30 до 60 тысяч рублей и с доходом свыше 60 тысяч рублей) Для каждой группы задается количество объектов, которые должны быть обследованы. Количество объектов, которые должны попасть в каждую из групп, задается, чаще всего, либо пропорционально заранее известной доле группы в генеральной совокупности, либо одинаковым для каждой группы. Внутри групп объекты отбираются произвольно. Квотные выборки используются в маркетинговых исследованиях достаточно часто. 2.2. Метод снежного кома Выборка строится следующим образом. У каждого респондента, начиная с первого, просятся контакты его друзей, коллег, знакомых, которые подходили бы под условия отбора и могли бы принять участие в исследовании. Таким образом, за исключением первого шага, выборка формируется с участием самих объектов исследования. Метод часто применяется, когда необходимо найти и опросить труднодоступные группы респондентов (например, респондентов, имеющих высокий доход, респондентов, принадлежащих к одной профессиональной группе, респондентов, имеющих какие-либо схожие хобби/увлечения и т.д.) 2.3 Стихийная выборка Опрашиваются наиболее доступные респонденты. Типичные примеры стихийных выборок – опросы в газетах/журналах, анкеты, отданные респондентам на самозаполнение, большинство интернет-опросов. Размер и состав стихийных выборок заранее не известен, и определяется только одним параметром – активностью респондентов. 2.4 Выборка типичных случаев Отбираются единицы генеральной совокупности, обладающие средним (типичным) значением признака. При этом возникает проблема выбора признака и определения его типичного значения.
Примеры ошибок выборки
Ошибка спецификации совокупности означает, что XYZ не понимает конкретных типов потребителей, которые должны быть включены в выборку. Если, например, XYZ создает группу людей в возрасте от 15 до 25 лет, многие из этих потребителей не принимают решение о покупке услуги потокового видео, потому что они не работают полный рабочий день. С другой стороны, если XYZ соберет выборку работающих взрослых, которые принимают решения о покупке, потребители в этой группе могут не смотреть 10 часов видеопрограмм каждую неделю.
Ошибка выбора также приводит к искажению результатов выборки, и типичным примером является опрос, в котором участвует лишь небольшая часть людей, которые сразу же откликаются. Если XYZ попытается связаться с потребителями, которые изначально не ответили, результаты опроса могут измениться. Кроме того, если XYZ исключает потребителей, которые не отвечают сразу, результаты выборки могут не отражать предпочтения всего населения.
Учет ошибок, не связанных с выборкой
XYZ также хочет избежать ошибок , не связанных с выборкой , которые вызваны человеческой ошибкой, например ошибкой, допущенной в процессе опроса. Если одна группа потребителей смотрит только пять часов видеопрограмм в неделю и включена в опрос, это решение является ошибкой, не связанной с выборкой. Предвзятые вопросы – это еще один тип ошибок.
-
История педагогики кратко шпаргалка
-
Режим реки лена кратко
-
Особенности учета процентов по долговым обязательствам в целях налогообложения кратко
-
Карамзин мнение русского гражданина кратко
- Африканская чума свиней кратко
Калькулятор расчета ошибки и размера выборки (для простой случайной выборки)
Пояснения к полям: Доверительная вероятность Вероятность того, что доверительный интервал накроет неизвестное истинное значение параметра, оцениваемого по выборочным данным. В практике исследований чаще всего используют 95%-ую доверительную вероятность Ошибка выборки (доверительный интервал) Интервал, вычисленный по выборочным данным, который с заданной вероятностью (доверительной) накрывает неизвестное истинное значение оцениваемого параметра распределения. Доля признака Ожидаемая доля признака, для которого рассчитывается ошибка. В случае, если данные о доле признака отсутствуют, необходимо использовать значение равное 50, при котором достигается максимальная ошибка.
Ошибка выборки (доверительный интервал)
Отклонение результатов, полученных с помощью выборочного наблюдения от истинных данных генеральной совокупности. Ошибка выборки бывает двух видов – статистическая и систематическая. Статистическая ошибка зависит от размера выборки. Чем больше размер выборки, тем она ниже. Пример: Для простой случайной выборки размером 400 единиц максимальная статистическая ошибка (с 95% доверительной вероятностью) составляет 5%, для выборки в 600 единиц – 4%, для выборки в 1100 единиц – 3% Обычно, когда говорят об ошибке выборки, подразумевают именно статистическую ошибку. Систематическая ошибка зависит от различных факторов, оказывающих постоянное воздействие на исследование и смещающих результаты исследования в определенную сторону. Пример:
В некоторых случаях, когда известны истинные распределения, систематическую ошибку можно нивелировать введением квот или перевзвешиванием данных, но в большинстве реальных исследований даже оценить ее бывает достаточно проблематично.
Малая выборка
Если численность выборочной совокупности
не более 30 единиц, то средняя ошибка
малой выборки при определении средней
величины рассчитывается по формуле:
|
при определении доли |
|
|
|
|
Для расчета ошибки малой выборки
применяется уточненная формула дисперсии
|
|
где n-1 — |
Типы задач выборочного наблюдения
-
определение ошибки выборки,
-
определение численности выборочной совокупности n,
-
определение вероятности того, что выборочная средняя (или доля) отклонится от генеральной не более, чем на заданную величину t=Δ/μ,
-
оценка случайности расхождений показателей выборочных наблюдений,
-
перенос выборочных характеристик на генеральную совокупность.
Проверка гипотез о средней и доле
Оценка случайности расхождений
показателей выборочных наблюдений
|
|
|
-
Если при n>30 коэффициент t<3, то делается вывод о случайности расхождений.
-
Если n≤ 30 , то полученное значение t сравнивают с табличным, определяемым по таблице распределения Стьюдента
-
Если
, расхождение считается существенным.
-
Если
, расхождение считается случайным.
Методы переноса выборочных данных на
генеральную совокупность
Задача 1
На основании результатов проведенного на заводе 5%
выборочного наблюдения (отбор случайный, бесповторный) получен следующий ряд
распределения рабочих по заработной плате:
| Группы рабочих по размеру заработной платы, тыс.р. | до 200 | 200-240 | 240-280 | 280-320 | 320 и выше | Итого |
| Число рабочих | 33 | 35 | 47 | 45 | 40 | 200 |
На основании приведенных данных определите:
1) с вероятностью 0,954 (t=2) возможные пределы, в которых
ожидается средняя заработная плата рабочего в целом по заводу (по генеральной
совокупности);
2) с вероятностью 0,997 (t=3) предельную ошибку и границы доли
рабочих с заработной платой от 320 тыс.руб. и выше.
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте WhatsAppTelegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Вычислим среднюю з/п: Для этого просуммируем произведения середин
интервалов и соответствующих частот, и полученную сумму разделим на сумму
частот.
2) Выборочная дисперсия:
Найдем доверительный интервал для средней. Предельная ошибка выборочной
средней считается по формуле:
где
—
аргумент функции Лапласа.
Искомые возможные пределы, в которых ожидается средняя заработная плата
рабочего в целом по заводу:
Найдем доверительный интервал для выборочной доли. Предельная ошибка
выборочной доли считается по формуле:
Доля рабочих с з/п от 320 тыс.р.:
Искомые границы доли рабочих с заработной платой от 320 тыс.руб. и выше:
Репрезентативность выборки
Свойство выборки корректно отражать генеральную совокупность. Одна и та же выборка может быть репрезентативной и нерепрезентативной для разных генеральных совокупностей. Пример:
- Выборка, целиком состоящая из москвичей, владеющих автомобилем, не репрезентирует все население Москвы.
- Выборка из российских предприятий численностью до 100 человек не репрезентирует все предприятия России.
- Выборка из москвичей, совершающих покупки на рынке, не репрезентирует покупательское поведение всех москвичей.
В то же время, указанные выборки (при соблюдении прочих условий) могут отлично репрезентировать москвичей-автовладельцев, небольшие и средние российские предприятия и покупателей, совершающих покупки на рынках соответственно
Важно понимать, что репрезентативность выборки и ошибка выборки – разные явления. Репрезентативность, в отличие от ошибки никак не зависит от размера выборки
Пример: Как бы мы не увеличивали количество опрошенных москвичей-автовладельцев, мы не сможем репрезентировать этой выборкой всех москвичей.
Определение численности выборки
Разрабатывая программу выборочного наблюдения, иногда задаются конкретным значением предельной ошибки с уровнем вероятности. Неизвестной остается минимальная численность выборки, обеспечивающая заданную точность. Ее можно получить из формул средней и предельной ошибок в зависимости от типа выборки. Так, подставляя и в и, решая ее относительно численности выборки, получим следующие формулы:
для повторной выборки n =
для бесповторной выборки n = .
Кроме того, при статистических величинах с количественными признаками надо знать и выборочную дисперсию, но к началу расчетов и она не известна. Поэтому она принимается приближенно одним из следующих способов (в приоритетном порядке):
- Берется из предыдущих выборочных наблюдений;
- Используется правило, согласно которому в размахе вариации укладывается примерно шесть стандартных отклонений (, а так как , то отсюда );
- Используется правило «трех сигм», согласно которому в средней величине укладывается примерно 3 стандартных отклонения (; отсюда ).
При изучении не численных признаков, если даже нет приблизительных сведений о выборочной доле, принимается w = 0,5, что по соответствует выборочной дисперсии в максимальном размере Дв = 0,5*(1-0,5) = 0,25.
Предыдущая лекция…Следующая лекция…
Другие статьи по данной теме:
- назад: Показатели вариации: понятие, виды, формулы для вычислений
- далее: Ряды динамики: понятие и классификация. Показатели уровней ряда
динамики. Примеры решения задач
Список использованных источников
- Белобородова С.С. и др. Теория статистики: Типовые задачи с контрольными заданиями.
Екатеринбург: Изд-во Урал. гос. экон. ун-та, 2001; - Минашкин В.Г. и др. Курс лекций по теории статистики. / Московский международный институт эконометрики,
информатики, финансов и права. — М., 2003; - Сизова Т.М. Статистика: Учебное пособие. – СПб.: СПб ГУИТМО, 2005;
- Фёдорова Л.Н., Фёдорова А.Е. Методические указания по написанию контрольной работы по курсу «Статистика»
для студентов экономических специальностей: УрГЭУ, 2007;
Понятие и виды выборочного наблюдения
Выборочное наблюдение применяется, когда применение сплошного наблюдения физически невозможно из-за большого массива данных или экономически нецелесообразно. Физическая невозможность имеет место, например, при изучении пассажиропотоков, рыночных цен, семейных бюджетов. Экономическая нецелесообразность имеет место при оценке качества товаров, связанной с их уничтожением, например, дегустация, испытание кирпичей на прочность и т.п.
Статистические единицы, отобранные для наблюдения, составляют выборочную совокупность или выборку, а весь их массив — генеральную совокупность (ГС). При этом число единиц в выборке обозначают n, а во всей ГС — N. Отношение n/N называется относительный размер или доля выборки.
Качество результатов выборочного наблюдения зависит от репрезентативности выборки, то есть от того, насколько она представительна в ГС. Для обеспечения репрезентативности выборки необходимо соблюдать принцип случайности отбора единиц, который предполагает, что на включение единицы ГС в выборку не может повлиять какой-либо иной фактор кроме случая.
Существует 4 способа случайного отбора в выборку:
- Собственно случайный отбор или «метод лото», когда статистическим величинам присваиваются порядковые номера, заносимые на определенные предметы (например, бочонки), которые затем перемешиваются в некоторой емкости (например, в мешке) и выбираются наугад. На практике этот способ осуществляют с помощью генератора случайных чисел или математических таблиц случайных чисел.
- Механический отбор, согласно которому отбирается каждая (N/n)-я величина генеральной совокупности. Например, если она содержит 100 000 величин, а требуется выбрать 1 000, то в выборку попадет каждая 100 000 / 1000 = 100-я величина. Причем, если они не ранжированы, то первая выбирается наугад из первой сотни, а номера других будут на сотню больше. Например, если первой оказалась единица № 19, то следующей должна быть № 119, затем № 219, затем № 319 и т.д. Если единицы генеральной совокупности ранжированы, то первой выбирается № 50, затем № 150, затем № 250 и так далее.
- Отбор величин из неоднородного массива данных ведется стратифицированным (расслоенным) способом, когда генеральная совокупность предварительно разбивается на однородные группы, к которым применяется случайный или механический отбор.
- Особый способ составления выборки представляет собой серийный отбор, при котором случайно или механически выбирают не отдельные величины, а их серии (последовательности с какого-то номера по какой-то подряд), внутри которых ведут сплошное наблюдение.
Качество выборочных наблюдений зависит и от типа выборки: повторная или бесповторная. При повторном отборе попавшие в выборку статистические величины или их серии после использования возвращаются в генеральную совокупность, имея шанс попасть в новую выборку. При этом у всех величин генеральной совокупности одинаковая вероятность включения в выборку.Бесповторный отбор означает, что попавшие в выборку статистические величины или их серии после использования не возвращаются в генеральную совокупность, а потому для остальных величин последней повышается вероятность попадания в следующую выборку.
Бесповторный отбор дает более точные результаты, поэтому применяется чаще. Но есть ситуации, когда его применить нельзя (изучение пассажиропотоков, потребительского спроса и т.п.) и тогда ведется повторный отбор.
Задача 3
С
целью определения средней месячной заработной платы персонала фирмы было
проведено 25%-ное выборочное обследование с отбором
единиц пропорционально численности типических групп. Для отбора сотрудников
внутри каждого филиала использовался механический отбор. Результаты
обследования представлены в следующей таблице:
| Номер филиала | Средняя месячная заработная плата, руб. | Среднее квадратическое отклонение, руб. | Число сотрудников, чел. |
| 1 | 870 | 40 | 30 |
| 2 | 1040 | 160 | 80 |
| 3 | 1260 | 190 | 140 |
| 4 | 1530 | 215 | 190 |
С
вероятностью 0,954 определите пределы средней месячной заработной платы всех
сотрудников гостиниц.
Решение
Предельная
ошибка выборочной средней:
Средняя
из внутригрупповых дисперсий:
Получаем:
Средняя
месячная заработная плата по всей совокупности филиалов:
Искомые
пределы средней месячной заработной платы:
Вывод к задаче
Собственно-случайная выборка
Отбор в этом случае производится либо по жребию, либо по таблицам случайных чисел.
На основании приемов классической выборки решаются следующие задачи:
а) определяются границы среднего значения показателя по генеральной совокупности;
б) определяются границы доли признака по генеральной совокупности.
Предельная ошибка средней при собственно-случайном отборе исчисляется по формулам:
а) при повторном отборе:
б) при бесповторном отборе:
где
– численность выборочной совокупности;
– численность генеральной совокупности;
– дисперсия признака;
– критерий кратности ошибки: при
; при
; при
.
Значения
определяются
по таблице функции Лапласа.
Границы (пределы) среднего значения признака по генеральной совокупности определяются следующим неравенством:
где
– среднее значение признака по выборочной совокупности.
Предельная ошибка доли при собственно-случайном отборе определяется по формулам:
а) при повторном отборе:
при бесповторном отборе:
где
– доля единиц совокупности с заданным значением признака в обзей численности выборки,
– дисперсия доли признака.
Границы (пределы) доли признака по всей (генеральной) совокупности определяются неравенством:
где
– доля признака по генеральной совокупности.