Доверительная вероятность простыми словами

Доверительная вероятность и доверительный интервал.

Вероятность того, что истинное значение измеряемой величины лежит внутри некоторого интервала, называется доверительной вероятностью, или коэффициентом надежности,а сам интервал — доверительным интервалом.

на так называемый коэффициент Стьюдента. Коэффициенты Стьюдента

n

Число измерений n	Доверительная вероятность y
0,67	0,90	0,95	0,99
2,0	6,3	12,7	63,7
1,3	2,4	3,2	5,8
1,2	2,1	2,8	4,6
1,2	2,0	2,6	4,0
1,1	1,8	2,3	3,3
1,0	1,7	2,0	2,6

Окончательно, для измеряемой величины y при заданной доверительной вероятности y и числе измерений n получается условие

Величину

случайной погрешностьюy.

Пример: см. лекцию №5 – ряд чисел.

При числе измерений – 45 и доверительной вероятности – 0,95 получим, что коэффициент Стьюдента приблизительно равен 2,15. Тогда доверительный интервал для данного ряда измерений равен 62,6.

Источником грубых погрешностей нередко бывают резкие изменения условий измерения и ошибки, допущенные оператором:

— неправильный отсчет по шкале измерительного прибора, происходящий из-за неверного учета цены малых делений шкалы;

— неправильная запись результата наблюдений, значений отдельных мер использованного набора, например, гирь;

— хаотические изменения параметров напряжения, питающего средства измерения, например, его амплитуды или частоты.

Доверительный интервал для среднего

Использование нормального распределения

Выборочное среднее имеет нормальное распределение, если объем выборки большой, поэтому можно применить знания о нормальном распределении при рассмотрении выборочного среднего.

В частности, 95% распределения выборочных средних находится в пределах 1,96 стандартных отклонений (SD) среднего популяции.

Когда у нас есть только одна выборка, мы называем это стандартной ошибкой среднего (SEM)  и вычисляем 95% доверительного интервала для среднего следующим образом:

Если повторить этот эксперимент несколько раз, то интервал будет содержать истинное среднее популяции в 95% случаев.

Обычно это доверительный интервал как, например, интервал значений, в пределах которого с доверительной вероятностью 95% находится истинное  среднее популяции (генеральное среднее).

Хотя это не вполне строго (среднее в популяции есть фиксированное значение и поэтому не может иметь вероятность, отнесённую к нему) таким образом интерпретировать доверительный интервал, но концептуально это удобнее для понимания.

Использование t-распределения

Можно использовать нормальное распределение, если знать  значение дисперсии в популяции. Кроме того, когда объем выборки небольшой, выборочное среднее отвечает нормальному распределению, если данные, лежащие в основе популяции, распределены нормально.

Если данные, лежащие в основе популяции, распределены ненормально и/или неизвестна генеральная дисперсия (дисперсия в популяции), выборочное  среднее подчиняется t-распределению Стьюдента.

Вычисляем 95% доверительный интервал для генерального среднего в популяции следующим образом:

t-

Вообще, она обеспечивает более широкий интервал, чем при использовании нормального распределения, поскольку учитывает дополнительную неопределенность, которую вводят, оценивая стандартное отклонение популяции и/или из-за небольшого объёма выборки.

Когда объём выборки большой (порядка 100 и более), разница между двумя распределениями (t-Стьюдента и нормальным) незначительна. Тем не менее всегда используют t-распределение при вычислении доверительных интервалов, даже если объем выборки большой.

Обычно указывают 95% ДИ. Можно вычислить другие доверительные интервалы, например 99% ДИ для среднего.

Вместо произведения стандартной ошибки и табличного значения t-распределения, которое соответствует двусторонней вероятности 0,05, умножают её (стандартную ошибку) на значение, которое соответствует двусторонней вероятности 0,01. Это более широкий доверительный интервал, чем в случае 95%, поскольку он отражает увеличенное доверие к тому, что интервал действительно включает среднее популяции.

Доверительный интервал

крайне мала и равна 0,003(1–0,997). Такие маловероятные события считаются практически невозможными, а потому величину

Выборочное наблюдение дает возможность определить среднюю арифметическую выборочной совокупности x и величину предельной ошибки этой средней ∆x, которая показывает с определенной вероятностью), насколько выборочная может отличаться от генеральной средней в большую или меньшую сторону. Тогда величина генеральной средней будет представлена интервальной оценкой, для которой нижняя граница будет равна

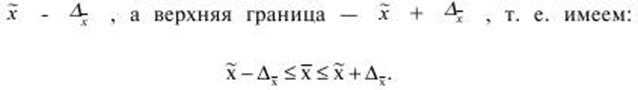
Интервал, в который с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра, называют доверительным, а вероятность Р – доверительной вероятностью. Чаще всего доверительную вероятность принимают равной 0,95 или 0,99, тогда коэффициент доверия t равен соответственно 1,96 и 2,58. Это означает, что доверительный интервал с заданной вероятностью заключает в себе генеральную среднюю.

Наряду с абсолютной величиной предельной ошибки выборки рассчитывается и относительная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности:

Чем больше величина предельной ошибки выборки, тем больше величина доверительного интервала и тем, следовательно, ниже точность оценки. Средняя (стандартная) ошибка выборки зависит от объема выборки и степени вариации признака в генеральной совокупности.

Функция ДОВЕРИТ

Возвращает значение, с помощью которого можно определить доверительный интервал для математического ожидания генеральной совокупности.

Доверительный интервал представляет собой диапазон значений. Выборочное среднее x является серединой этого диапазона, следовательно, доверительный интервал определяется как (x ± ДОВЕРИТ). Например, если x — это среднее выборочное значение времени доставки товаров, заказанных по почте, то математическое ожидание генеральной совокупности принадлежит интервалу (x ± ДОВЕРИТ).

Для любого значения математического ожидания генеральной совокупности μ0, находящегося в этом интервале, вероятность того, что выборочное среднее отличается от μ0 более чем на x, превышает значение уровня значимости «альфа». Для любого математического ожидания μ0, не относящегося к этому интервалу, вероятность того, что выборочное среднее отличается от μ0 более чем на x, не превышает значения уровня значимости «альфа». Например, предположим, что требуется при заданном выборочном среднем x, стандартном отклонении генеральной совокупности и размере выборки создать критерий на основе двойной выборки при уровни значимости «альфа» для проверки гипотезы о том, согласно которой, математическое ожидание равно μ0. В этом случае гипотеза не отвергается, если μ0 принадлежит доверительному интервалу, и отвергается, если μ0 не принадлежит доверительному интервалу. Доверительный интервал не позволяет предполагать, что с вероятностью (1 альфа) время доставки следующей посылки окажется в пределах доверительного интервала.

Синтаксис

ДОВЕРИТ(альфа ;станд_откл;размер)

Альфа — уровень значимости, используемый для вычисления уровня надежности. Уровень надежности равняется 100*(1 — альфа) процентам или, другими словами, значение аргумента «альфа», равное 0,05, означает 95-процентный уровень надежности.

Станд_откл — стандартное отклонение генеральной совокупности для интервала данных, предполагается известным.

Размер — размер выборки.

Замечания

·        Если какой-либо из аргументов не является числом, функция ДОВЕРИТ возвращает значение ошибки #ЗНАЧ!.

·        Если альфа ≤ 0 или альфа ≥ 1, функция ДОВЕРИТ возвращает значение ошибки #ЧИСЛО!.

·        Если станд_откл ≤ 0, функция ДОВЕРИТ возвращает значение ошибки #ЧИСЛО!.

·        Если значения аргумента «размер» не является целым числом, то оно усекается.

·        Если размер < 1, функция ДОВЕРИТ возвращает значение ошибки #ЧИСЛО!.

·        Если предположить, что альфа = 0,05, то нужно определить ту часть стандартной нормальной кривой, которая равна (1 — альфа), или 95 процентам. Это значение равно ± 1,96. Следовательно, доверительный интервал, следовательно, определяется по формуле:

<<<<предыдущая || оглавление || следующая>>

Построить ряд распределения

Предположим, мы имеем 100 значений и все разные, например: масса тела Сомалийских пиратов.
Такой набор данных обрабатывать неудобно, мы даже не можем представить их на обычном графике.
Поэтому нам необходимо категоризировать имеющиеся данные и для этого мы делаем следующее:

Запишем наши данные в таблицу:

Таблица 3. Вес сомалийских пиратов
132	65	139	116	83	71	71	120	111	64
75	125	90	102	115	127	115	114	122	144
107	89	66	93	146	139	81	68	79	123
79	82	63	127	71	103	102	67	116	118
132	90	131	127	101	123	73	112	127	104
80	84	103	67	105	138	129	110	90	99
87	138	117	104	79	79	112	116	106	71
122	70	105	99	71	82	102	91	87	90
83	89	84	102	80	78	147	130	138	124
138	88	146	96	118	101	128	87	111	115

Данные разобьём на группы, для начала предлагаю разбить на одиннадцать интервалов:

Теперь посчитаем количество пиратов (весов, я имею ввиду) в каждом интервале:

#	Интервал	Количество элементов
Таблица 4. Количество элементов в интервалах
1.	63 — 70.64	8
2.	70.64 — 78.28	8
3.	78.28 — 85.92	13
4.	85.92 — 93.56	12
5.	93.56 — 101.2	5
6.	101.2 — 108.84	12
7.	108.84 — 116.48	12
8.	116.48 — 124.12	9
9.	124.12 — 131.76	9
10.	131.76 — 139.4	8
11.	139.4 — 147.04	4

Вуа-ля, наше распределение на графике:

График 11. Ряд распределения массы тела сомалийских пиратов

Бонус

Интервалы лучше брать целыми числами, поэтому, если с выбранным количеством интервалов
размер выходит нецелым, то можно раздвинуть диапазон значений, пример:

Диапазон можно двигать как вверх, так и вниз, но лучше в обе стороны.

Совет

Принято делить распределение на 7-8 интервалов, но в каждой конкретной ситуации
Вы можете выбрать отличное количество интервалов, впрочем, как и сделать их
различной длины.

Этап 2. Обработка исходной выборки

Обработка выборки методами статистики требует вычисления следующих значений:

1. Среднее арифметическое значение

2. Медиана — число, характеризующее выборку: ровно половина элементов выборки больше медианы, другая половина меньше медианы

(для выборки, имеющей нечетное число значений)

3. Размах — разница между максимальным и минимальным значениями в выборке

4. Дисперсия — используется для более точного оценивания вариации данных

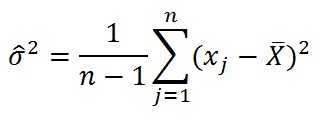
5. Среднеквадратическое отклонение по выборке (далее — СКО) — наиболее распространённый показатель рассеивания значений корректировок вокруг среднего арифметического значения.

6. Коэффициент вариации — отражает степень разбросанности значений корректировок

7. коэффициент осцилляции — отражает относительное колебание крайних значений цен в выборке вокруг средней

Таблица 2. Статистические показатели исходной выборки

Коэффициент вариации, который характеризует однородность данных, составляет 12,29%, однако коэффициент осцилляции слишком велик. Таким образом, мы можем утверждать, что исходная выборка не является однородной, поэтому перейдем к расчету доверительного интервала.

Типы доверительных интервалов

Существует много типов доверительных интервалов. Вот наиболее часто используемые:

Доверительный интервал для среднего

Доверительный интервал для среднего значения — это диапазон значений, который может содержать среднее значение генеральной совокупности с определенным уровнем достоверности. Формула для расчета этого интервала:

Доверительный интервал = x +/- z*(s/ √n )

куда:

• x : выборочное среднее
• z: выбранное значение z
• s: стандартное отклонение выборки
• n: размер выборки

Ресурсы: Как рассчитать доверительный интервал для среднегоДоверительный интервал для среднего калькулятора

Доверительный интервал для разницы между средними значениями

Доверительный интервал (ДИ) для разницы между средними значениями представляет собой диапазон значений, который, вероятно, содержит истинное различие между двумя средними значениями генеральной совокупности с определенным уровнем достоверности. Формула для расчета этого интервала:

Доверительный интервал = ( x 1 – x 2 ) +/- t * √ ((s p 2 /n 1 ) + (s p 2 /n 2 ))

куда:

• x 1 , x 2 : среднее значение для образца 1, среднее значение для образца 2
• t: t-критическое значение, основанное на доверительном уровне и (n 1 +n 2 -2) степенях свободы
• s p 2 : объединенная дисперсия
• n 1 , n 2 : размер выборки 1, размер выборки 2

куда:

• Объединенная дисперсия рассчитывается как: s p 2 = ((n 1 -1)s 1 2 + (n 2 -1)s 2 2 ) / (n 1 +n 2 -2)
• Критическое значение t можно найти с помощью калькулятора обратного t-распределения .

Ресурсы: Как рассчитать доверительный интервал для разницы между среднимиДоверительный интервал для калькулятора разницы между средними значениями

Доверительный интервал для пропорции

Доверительный интервал для доли — это диапазон значений, который может содержать долю населения с определенным уровнем достоверности. Формула для расчета этого интервала:

Доверительный интервал = p +/- z * (√ p (1-p) / n )

куда:

• p: доля выборки
• z: выбранное значение z
• n: размер выборки

Ресурсы: Как рассчитать доверительный интервал для пропорцииДоверительный интервал для калькулятора пропорций

Доверительный интервал для разницы в пропорциях

Доверительный интервал для разницы в пропорциях — это диапазон значений, который может содержать истинную разницу между двумя пропорциями населения с определенным уровнем достоверности. Формула для расчета этого интервала:

Доверительный интервал = (p 1 –p 2 ) +/- z*√(p 1 (1-p 1 )/n 1 + p 2 (1-p 2 )/n 2 )

куда:

• p 1 , p 2 : доля образца 1, доля образца 2
• z: z-критическое значение, основанное на доверительном уровне
• n 1 , n 2 : размер выборки 1, размер выборки 2

Ресурсы: Как рассчитать доверительный интервал для разницы пропорцийДоверительный интервал для калькулятора разницы пропорций

Математическое описание

Смотря на закон распределения, мы можем понять, какова вероятность того или иного события,
можем сказать, какова вероятность, что произойдёт группа событий, а в этой статье мы рассмотрим, как наши выводы «на глаз» перевести
в математически обоснованное утверждение.

Крайне важное определение: математическое ожидание — это площадь под графиком распределения. Если мы говорим о дискретном распределении —
это сумма событий умноженных на соответсвующие вероятности, также известно как момент:. Момент степени k:

Момент степени k:

Центральный момент степени k:

Среднее значение

Среднее значение (μ) закона распределения — это математическое ожидание случайной величины
(случайная величина — это событие), например, сколько в среднем посетителей заходит в магазин в час:

Кол-во посетителей	1	2	3	4	5	6
Таблица 1. Количество посетителей в час
Количество наблюдений	92	154	74	12	15	26	27

График 1. Количество посетителей в час

Чтобы найти среднее значение всех результатов необходимо сложить всё вместе и разделить на количество результатов:

То же самое мы можем проделать используя формулу 2:

Собственно, формула 2 представляет собой среднее арифметическое всех значений Итог: в среднем, 1.73 посетителя в час

Количество посетителей	1	2	3	4	5	6
Таблица 2. Закон распределения количества посетителей
Вероятность (%)	23	38.5	18.5	3	3.8	6.5	6.8

Отклонение от среднего

Посмотрите на это распределение, можно предположить, что в среднем случайная величина равна 100±5, поскольку
кажется, что таких значений несравнимо больше чем тех, что меньше 95 или больше 105:

График 2. График функции вероятности. Распределение ≈ 100±5

Среднее значение по формуле (2): μ = 99.95, но как посчитать, насколько далеко все значения находятся от среднего? Вам должна быть
знакома запись 100±5. Что бы получить это значение ±, нам необходимо определить диапазон значений вокруг среднего. И мы могли бы
использовать в качестве меры удалённости «разность» между средним и случайными величинами:

но сумма таких расстояний, а следовательно и любое производное от этого числа, будет равно нулю, поэтому в качестве меры выбрали квадрат разниц
между величинами и средним значением:

Соответственно, среднее значение удалённости — это математическое ожидание квадратов удалённости:

σ возведена в квадрат, поскольку вместо расстояний мы взяли квадрат расстояний. σ2 называется дисперсией. Корень из дисперсии
называется средним квадратическим отклонением, или среднеквадратическим отклоненим, и его используют в качестве меры разброса:

Возвращаясь к примеру, посчитаем среднеквадратическое отклонение для графика 2:

Определение оптимального сочетания доверительного интервала и доверительной вероятности

Предложена методика расчета оптимального доверительного интервала и доверительной вероятности для произвольной выборки. Для этого использован способ, основанный на максимизации среднего приращения информации о выборке, который позволяет учесть такой показатель, как неопределенность исходной информации. Проведен численный эксперимент, в ходе которого исследована связь оптимальной доверительной вероятности и доверительного интервала от размера выборки, закона распределения случайной величины и типа неопределенности. Установлены численные значения размера выборки, при достижении которых осуществляется переход от детерминированного типа неопределенности к стохастическому типу, а затем к нечеткому.

Асимптотическое приближение

Однако не всегда можно рассчитать точный доверительный интервал. В этом случае строится приближённая вероятность — асимптотическая. Пусть для некоторого j Є (0,1) существует набор статистик S-(X|n|, j) и S-(X|n|, j), причём такие, что lim P

Отсюда получают оценку: p = m / n. Теперь нужно убедиться, что p максимизирует функцию правдоподобия. То есть d2LnL / dp2 = — m / p2 — (n — m) / (1 — p)2 Использование онлайн-калькулятора

На практике довольно часто вычислить доверительную область не так уж и просто. Всё дело в том, что высокая вероятность часто находится в выборке большого объёма, поэтому приходится выполнять громоздкие вычисления. Учитывая, что доверительная вероятность определяет точность полученных результатов, другими словами, показывает, с какой вероятностью неправильное решение попадает в найденный интервал, обычно используют процент выборки от 95 до 99,9%.

Для высокой точности получения диапазона как раз и используют сервисы, которые в последнее время начали называться онлайн-калькуляторами. Это специализированные сайты, умеющие в автоматическом режиме решать различные математические задания. Особенность этих сайтов в том, что они предоставляют услуги бесплатно, при этом от их пользователей не требуется никаких знаний.

Всё что им нужно — это ввести в пролагаемую форму данные и нажать кнопку «Рассчитать». Система автоматически вычислит ответ и выведет его на экран. Из наиболее популярных можно отметить следующие сервисы:

Еще термины по предмету «Автоматизация технологических процессов»

Абсолютная величина (в статистике)

форма количественного выражения статистических показателей, непосредственно характеризующая размеры (абсолютные) социально – экономических явлений, их признаков в единицах меры протяженности, площади, массы (веса) и т.п., в единицах счета времени, в денежных единицах или в виде числа элементов (единиц), составляющих данное массовое явление, изучаемое статистикой и называемое совокупностью статистической. Различают абсолютные величины: 1) индивидуальные, относящиеся к отдельным единицам совокупности; групповые и общие, отображающие размеры 2) признака или число единиц соответственно в отдельных частях совокупности или в совокупности в целом.

Автоматизированная система государственной статистики (АСГС)

межотраслевая многоуровневая автоматизированная система сбора и обработки учетностатистической информации, необходимой для планирования и управления народным хозяйством. АСГС создавалась как одно из важнейших функциональных звеньев Общегосударственной автоматизированной системы сбора и обработки информации для учета, планирования и управления народным хозяйством (ОГАС), осуществляла интеграцию учётно-статистической информации и взаимодействовала с различными ее звеньями.

Автоматическое средство измерений

средство измерений, производящее без непосредственного участия человека измерения и все операции, связанные с обработкой результатов измерений, их регистрацией, передачей данных или выработкой управляющего сигнала.

• Вероятность доверительная

• Доверительность

• Вероятность

• Доверительные границы

• Доверительные операции

• Доверительная граница

• Эффект доверительности

• Доверительный интервал

• Интервал доверительный

• Доверительное множество

• Управляющий доверительный

• Доверительная собственность

• Доверительное управление

• Собственник доверительный

• Доверительный управляющий

• Управление доверительное

• Вероятная эволюция

• Вероятность объективная

• Вероятность субъективная

• Вероятность восстановления

Этап 4. Анализ разных способов расчета доверительного интервала

Два способа расчета доверительного интервала — через медиану и коэффициент Стьюдента — привели к разным значениям интервалов. Соответственно, получилось две различные очищенные выборки.

Таблица 3. Статистические показатели по трем выборкам.

Показатель	Исходная выборка	1 вариант	2 вариант
Среднее значение
Дисперсия
Коэф. вариации
Коэф. осциляции
Количество выбывших объектов, шт.

На основании выполненных расчетов можно сказать, что полученные разными методами значения доверительных интервалов пересекаются, поэтому можно использовать любой из способов расчета на усмотрение оценщика.

Однако мы считаем, что при работе в системе estimatica.pro целесообразно выбирать метод расчета доверительного интервала в зависимости от степени развитости рынка:

• если рынок неразвит, применять метод расчета через медиану и среднеквадратическое отклонение, так как количество выбывших объектов в этом случае невелико;
• если рынок развит, применять расчет через критическое значение t-статистики (коэффициент Стьюдента), так как есть возможность сформировать большую исходную выборку.

При подготовке статьи были использованы:

1. Грибовский С.В., Сивец С.А., Левыкина И.А. Математические методы оценки стоимости имущества. Москва, 2014 г.

2. Данные системы estimatica.pro

Анализ случайных
погрешностей основывается на теории
случайных ошибок, дающей возможность
с определенной гарантией вычислить
действительное значение измеренной
величины и оценить возможные ошибки.

Основу теории
случайных ошибок составляют следующие
предположения:

при большом числе
измерений случайные погрешности
одинаковой величины, но разного знака
встречаются одинаково часто;

большие погрешности
встречаются реже, чем малые (вероятность
появления погрешности уменьшается с
ростом ее величины);

при бесконечно
большом числе измерении истинное
значение измеряемой величины равно
среднеарифметическому значению всех
результатов измерений;

появление того
или иного результата измерения как
случайного события описывается нормальным
законом распределения.

На практике
различают генеральную и выборочную
совокупность измерений.

Под генеральной
совокупностью


подразумевают все множество возможных
значений измерений
или возможных значений погрешностей.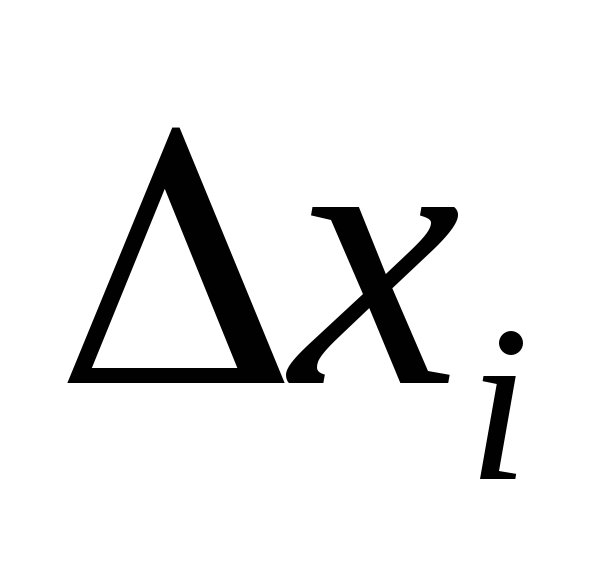

Для выборочной
совокупности


число измерений
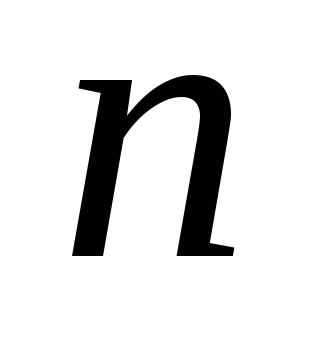ограничено, и в каждом конкретном случае
строго определяется. Считают, что, если,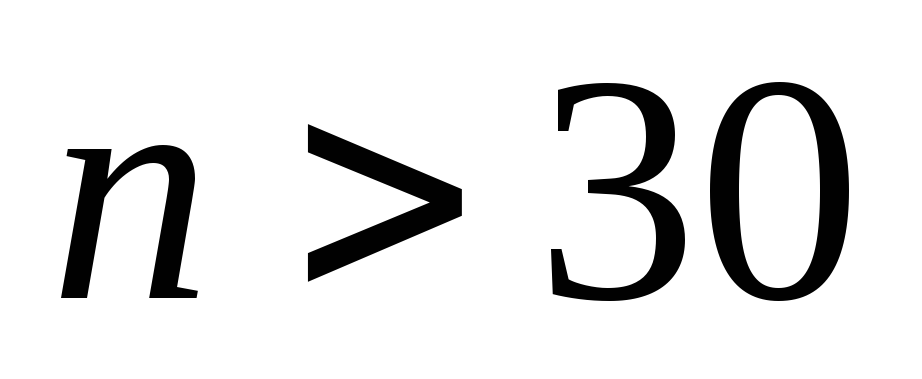
то среднее значение данной совокупности
измерений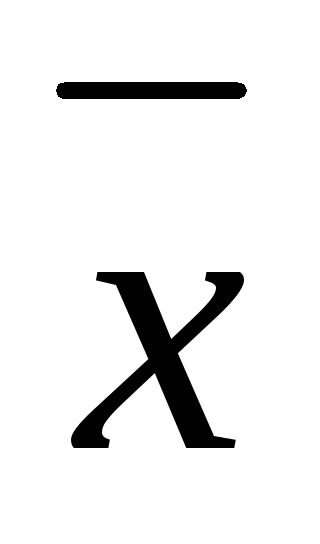достаточно приближается к его истинному
значению.

Пример (6) оценки инвестиционным менеджером чистого притока денежных средств клиентов.

Инвестиционный менеджер хочет построить 95-процентный доверительный интервал для притоков и оттоков денежных средств своих клиентов в течение следующих 6 месяцев.

Он начинается с обзвона случайной выборки из 10 клиентов, чтобы опросить их о планируемых взносах и изъятиях средств из инвестиционного фонда.

Затем менеджер вычисляет изменение денежного потока для каждого клиента из выборки, как процентное изменение от общего объема средств, размещенных у менеджера. Положительное процентное изменение указывает на чистый приток денежных средств на счет клиента, а отрицательное процентное изменение указывает на чистый отток денежных средств со счета клиента.

Менеджер взвешивает каждый ответ клиента по относительному размеру счета в рамках выборки, а затем вычисляет взвешенное среднее.

Проделав все это, инвестиционный менеджер вычисляет взвешенное среднее значение равное 5.5%. Таким образом, проведенная точечная оценка означает, что общая сумма средств под управлением менеджера увеличится на 5.5% в течение следующих 6 месяцев.

Стандартное отклонение наблюдений в выборке составляет 10%. Гистограмма прошлых данных выглядит довольно близко к нормальному распределению, так что менеджер предполагает, что генеральная совокупность также соответствует нормальному распределению.

1. Рассчитайте 95-процентный доверительный интервал для среднего по совокупности и интерпретируйте результаты.

Менеджер решил проанализировать, каким будет доверительный интервал, если использовать размер выборки 20 или 30, и получил то же самое среднее (5.5%) и стандартное отклонение (10%).

2. Используя выборочное среднее 5.5% и стандартное отклонение 10%, вычислите доверительный интервал для размеров выборки от 20 до 30. Для размера выборки 30 используйте Формулу 6.

3. Интерпретируйте результаты для частей 1 и 2.

Решение для части 1:

Поскольку совокупность неизвестна, а размер выборки мал, менеджер должен использовать t-статистику из Формулы 6 для расчета доверительного интервала.

Для выборки размера 10, (rm{df} = n — 1 = 10 — 1 = 9).

Для 95-процентного доверительного интервала, он должен использовать значение (t_{0.025}) для df = 9.

В соответствии с таблицами распределения Стьюдента это значение равно 2.262.

Таким образом, 95-процентный доверительный интервал для среднего значения по совокупности равен:

( begin{aligned} overline X pm t_{0.025} {s over sqrt{n}} &= 5.5% pm 2.262 {10% over sqrt {10}} \ &= 5.5% pm 2.262(3.162) \ &= 5.5% pm 7.15% end{aligned} )

Доверительный интервал для среднего по совокупности охватывает значения -1.65% до + 12,65%.

Мы предположили, что в этом примере размер выборки достаточно мал по сравнению с размером клиентской базы, поэтому мы можем пренебречь поправкой для конечной совокупности.

Менеджер может быть уверен на 95%, что этот диапазон включает в себя среднее значение по совокупности.

Решение для части 2:

В Таблице 4 приведены расчеты для выборок трех размеров.

Распределение	95% доверительный интервал	Нижняя граница	Верхняя граница	Относительный размер
( t(n = 10) )	(5.5% pm 2.262(3.162) )	-1.65%	12.65%	100.0%
( t(n = 20) )	(5.5% pm 2.093(2.236) )	0.82	10.18	65.5
( t(n = 30) )	(5.5% pm 2.045(1.826) )	1.77	9.23	52.2

Решение для части 3:

Ширина доверительного интервала уменьшается по мере увеличения размера выборки. Это уменьшение является функцией стандартной ошибки, которая становится меньше при увеличении (n).

Коэффициент надежности также становится меньше, так как число степеней свободы возрастает.

В последней колонке Таблицы 4 показан относительный размер ширины доверительных интервалов, если принять (n = 10 ) за 100%. Размер выборки 20 уменьшает ширину доверительного интервала до 65.5% от ширины интервала для размера выборки 10.

При размере выборки 30 ширина интервала сокращается почти в два раза. На основе этих данных, инвестиционный менеджер получил бы наиболее точные результаты, используя размер выборки 30.

Рассмотрев многие из фундаментальных понятий статистической выборки и оценки, мы можем сосредоточить внимание на вопросах отбора выборки, представляющих особый интерес для финансовых аналитиков. Качество выводов зависит от качества данных, а также от качества используемого плана выборки

Финансовые данные создают особые проблемы, и планы выборки часто отражают одну или несколько систематических ошибок (смещений). В следующем разделе этого чтения обсуждаются эти вопросы.

См. далее:

• CFA — Систематическая ошибка добычи данных (дата-майнинга)
• CFA — Систематическая ошибка выборки, ошибки опережения и временного периода

Интервальная оценка с помощью доверительной вероятности

Для большой
выборки и нормального закона распределения
общей оценочной характеристикой
измерения являются дисперсия
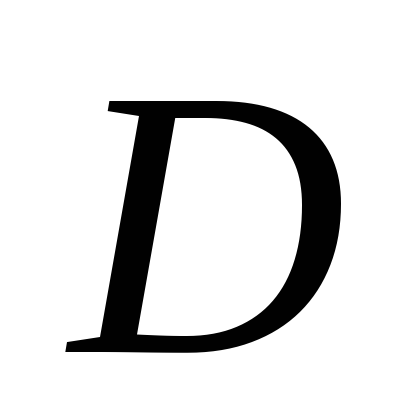и коэффициент вариации:

;
.
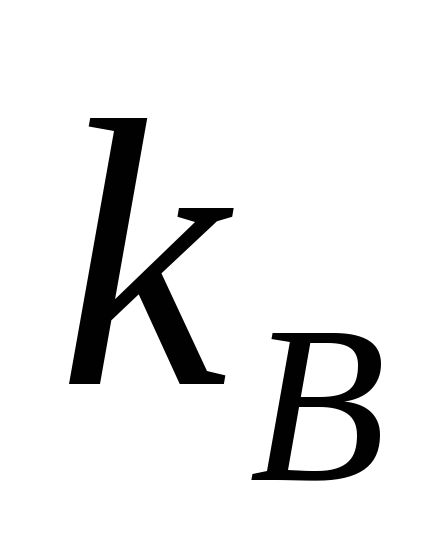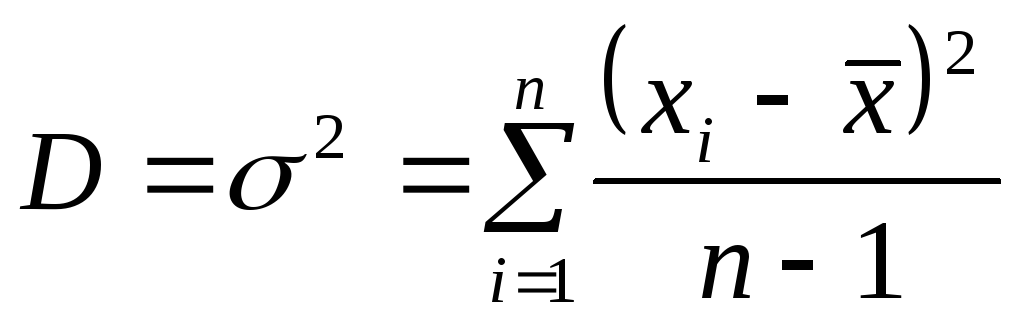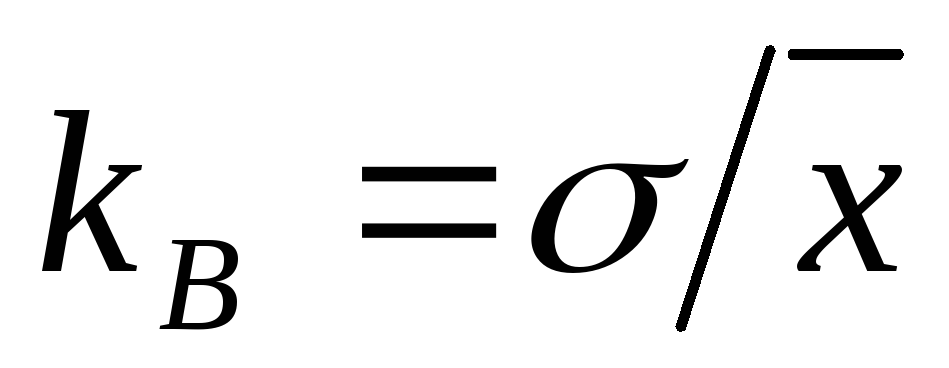(1.1)

Дисперсия
характеризует однородность измерения.
Чем выше
,
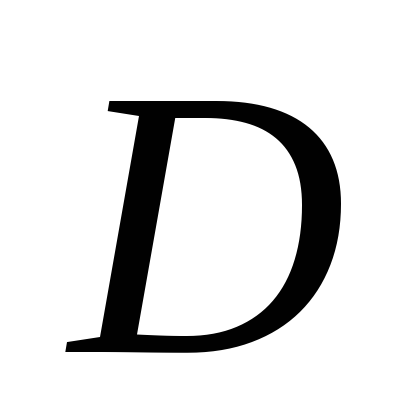тем больше
разброс измерений.

Коэффициент
вариации характеризует изменчивость.
Чем выше
,
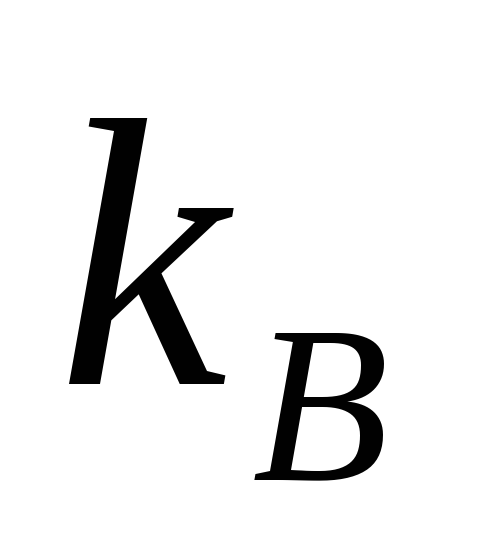тем больше
изменчивость измерений относительно
средних значений.

Для оценки
достоверности результатов измерений
вводятся в рассмотрение понятия
доверительного интервала и доверительной
вероятности.

Доверительным


называется
интервал


значений
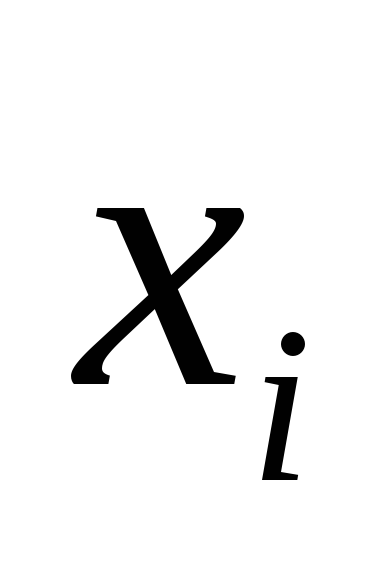,в который
попадает истинное значение
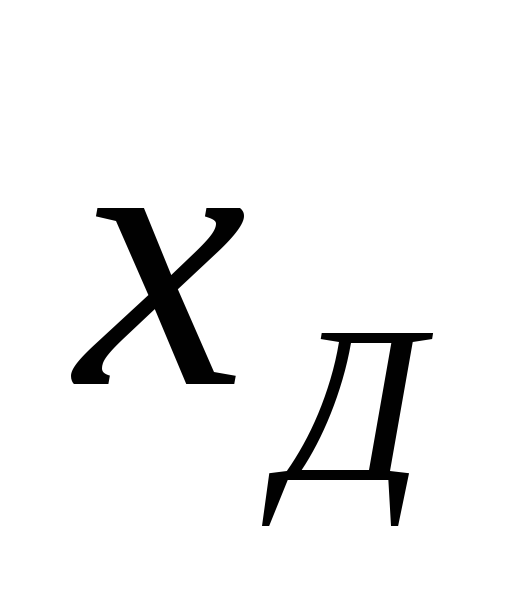измеряемой величины с заданной
вероятностью.

Доверительной
вероятностью


(достоверностью) измерения называется
вероятность того, что истинное значение
измеряемой величины попадает в данный
доверительный интервал, т.е. в зону
.
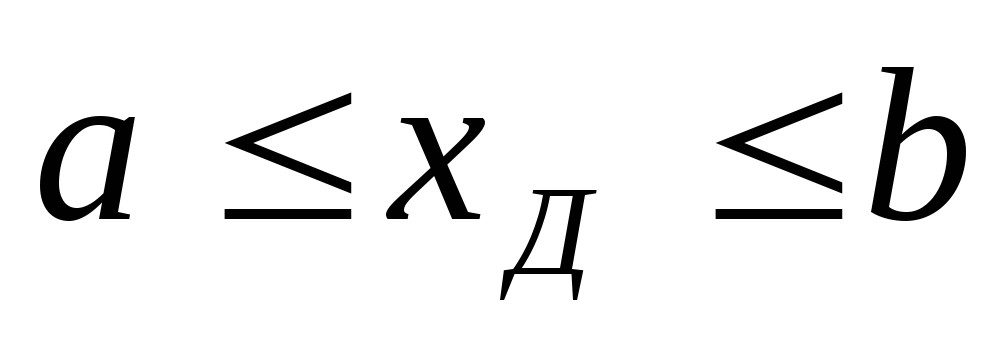Эта величина определяется в долях
единицы или в процентах

,

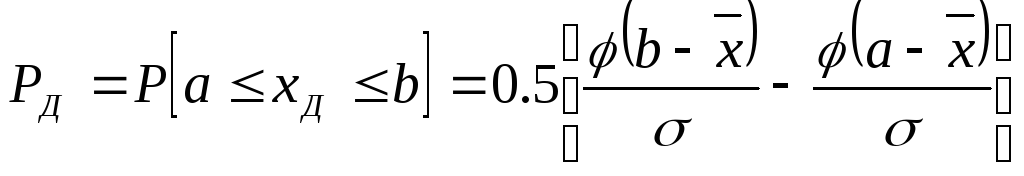где
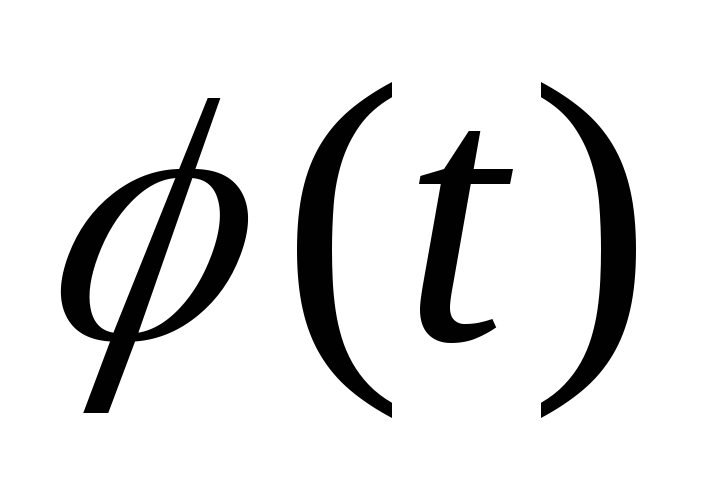— интегральная функция Лапласа (табл.1.1

)

Интегральная
функция Лапласа определяется следующим
выражением:

.

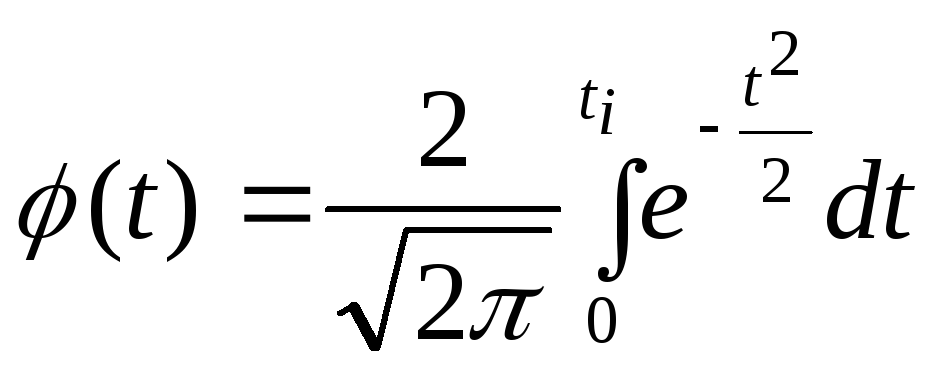Аргументом этой
функции является гарантийный
коэффициент

:

Таблица
1.1

Общий обзор

Взяв выборку из популяции, мы получим точечную оценку интересующего нас параметра и вычислим стандартную ошибку для того, чтобы указать точность оценки.

Однако, для большинства случаев стандартная ошибка как такова не приемлема. Гораздо полезнее объединить эту меру точности с интервальной оценкой для параметра популяции.

Это можно сделать, используя знания о теоретическом распределении вероятности выборочной статистики (параметра) для того, чтобы вычислить доверительный интервал (CI – Confidence Interval, ДИ – Доверительный интервал) для параметра.

Вообще, доверительный интервал расширяет оценки в обе стороны некоторой величиной, кратной стандартной ошибке (данного параметра); два значения (доверительные границы), определяющие интервал, обычно отделяют запятой и заключают в скобки.