"краткий курс геометрии 7 класс"

Уроки

Треугольники

Высота равностороннего треугольникаNEW

+ тестирование

Высота треугольникаNEW

+ тестирование

Длина медианы правильного треугольникаNEW

+ тестирование

Длина средней линии треугольникаNEW

+ тестирование

Медиана равностороннего треугольникаNEW

+ тестирование

Медиана треугольникаNEW

+ тестирование

Неравенство треугольникаNEW

+ тестирование

Остроугольный треугольникNEW

+ тестирование

Площадь правильного треугольникаNEW

+ тестирование

Площадь прямого треугольникаNEW

+ тестирование

Площадь прямоугольного треугольникаNEW

+ тестирование

Площадь равнобедренного треугольникаNEW

+ тестирование

Площадь равностороннего треугольникаNEW

+ тестирование

Правильный треугольникNEW

+ тестирование

Равнобедренный тупоугольный треугольникNEW

+ тестирование

Свойства прямоугольного треугольникаNEW

+ тестирование

Средняя линия прямоугольного треугольникаNEW

+ тестирование

Средняя линия прямоугольного треугольникаNEW

+ тестирование

Стороны прямоугольного треугольникаNEW

+ тестирование

Тупоугольный треугольникNEW

+ тестирование

Параллельные прямые

Аксиома параллельных прямыхNEW

+ тестирование

Параллельные прямыеNEW

+ тестирование

Признаки параллельных прямыхNEW

+ тестирование

Свойства параллельных прямыхNEW

+ тестирование

Соотношения между сторонами и углами треугольника

Биссектриса равнобедренного треугольникаNEW

+ тестирование

Боковая сторона равнобедренного треугольникаNEW

+ тестирование

Внешний угол треугольникаNEW

+ тестирование

Высота равнобедренного треугольникаNEW

+ тестирование

Гипотенуза равнобедренного треугольникаNEW

+ тестирование

Свойства внешнего угла треугольникаNEW

+ тестирование

Стороны равнобедренного треугольникаNEW

+ тестирование

Сумма углов прямоугольного треугольникаNEW

+ тестирование

Основные понятия

Приветствуем вас уважаемые школьники. В этом обучающем видео уроке по школьному предмету Геометрия за 7 класс, мы с Вами узнаем основные понятия данного предмета.

Геометрия 7 класс. Основные понятия.

С геометрией мы встречались в пятом и шестом классе, если выразиться обобщенно, это наука, которая изучает фигуры, их свойства. Сейчас, приступая к более глубокому изучению геометрии, нужно выйти на новый уровень этой науки, более строгий и более четкий, разобрать ее базовые понятия и аксиомы. Это нужно для того, чтобы начать изучать базовые объекты, которые необходимо определять, т. е. доказывать, и на которых мы будем строить дальнейшие определения.

Более подробно об уроке и задании решения можете узнать на сайте http://interneturok.ru

Базовые понятия

Базовые понятия геометрии, которые не нужно определять: точка, прямая, плоскость. На этих базовых понятиях строятся другие понятия. Рассмотрим это на определении луча. Луч – это часть прямой, ограниченная с одной стороны точкой. Из базовых понятий точка и прямая мы вывели понятие луча (рис. 1).

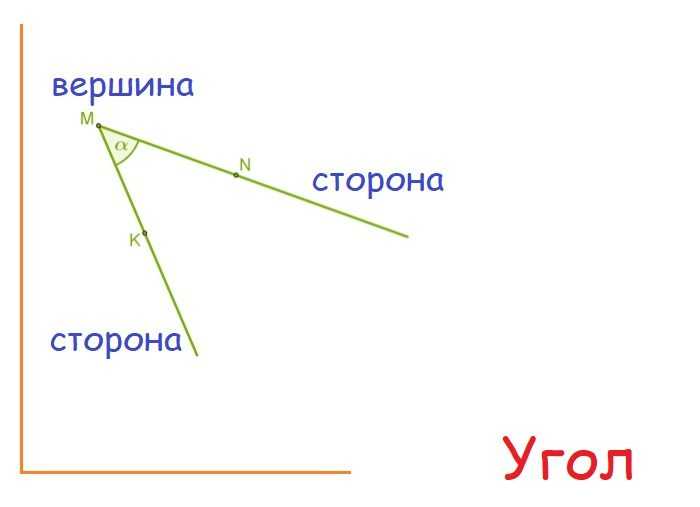
Аналогично, зная определение луча, можно дать определение угла. Угол – это геометрическая фигура, образованная двумя лучами, имеющими общую вершину (рис. 2).

Так можно поэтапно дать определение треугольнику, четырехугольнику, равенству треугольников и т. д.

Также нужно, кроме определений, уметь доказывать различные утверждения. Например, мы знаем, что сумма углов треугольника равна 180о, чтобы это доказать, нужно построить цепь верных определений, которые приведут к тому, что сумма углов треугольника равна 180о.

Аксиома

Аксиома – это заведомо истинное утверждение, принимаемое без доказательств.

Пример аксиомы:

Через любые две точки можно провести прямую и только одну (рис. 3).

Структура геометрии (планиметрии)

Дальнейшие утверждения могут быть выведены из аксиом, их называют теоремами (утверждения которые можно доказать), а уже из теорем получают следствия теорем.

Геометрия построена так, что в основании лежат базовые понятия (которые не нужно доказывать) и аксиомы, из них выводятся следующие понятия (первичные теоремы) и так по цепочке, сложнее и сложнее, это все развивается в науку.

Из программы геометрии пятого, шестого класса мы знаем, что площадь квадрата равна квадрату его стороны, но почему это именно так, можно будет разобрать в процессе изучения геометрии седьмого класса. Мы введем понятия площади, квадрата, угла, градуса, треугольника и т. д., докажем соответствующие теоремы, чтобы потом ими можно было пользоваться, объясняя более сложные теоремы и следствия теорем по цепочке, от фундамента базовых понятий и аксиом.

Заключение

На сегодняшнем уроке мы узнали структуру геометрии, разобрали, на каких понятиях она базируется.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Festival.1september.ru (Источник).
Festival.1september.ru (Источник).
Festival.1september.ru (Источник).

Домашнее задание

Ознакомьтесь самостоятельно с аксиомами геометрии (планиметрии)
Если две прямые имеют общую точку, то как они находятся относительно друг друга на плоскости?
Докажите теорему: через каждую точку прямой можно провести перпендикулярную ей прямую, и притом только одну.

Мне нравится1Не нравится

Геометрия 7 класс объяснение основных тем, понятно для детей

первые геометрические объекты

Начать стоит с самого понятия «геометрия». С древнегреческого слово переводится как земля и измерение. Эта древнейшая наука, которая появилась в связи с необходимостью строить здания, дороги, измерять объекты и прокладывать границы.

Первыми геометрическими фигурами, которые стоит усвоить, являются точка, прямая, отрезок.
Точка — это абстрактный объект в пространстве. Никаких измерительных характеристик она не имеет (но можно определить координаты).

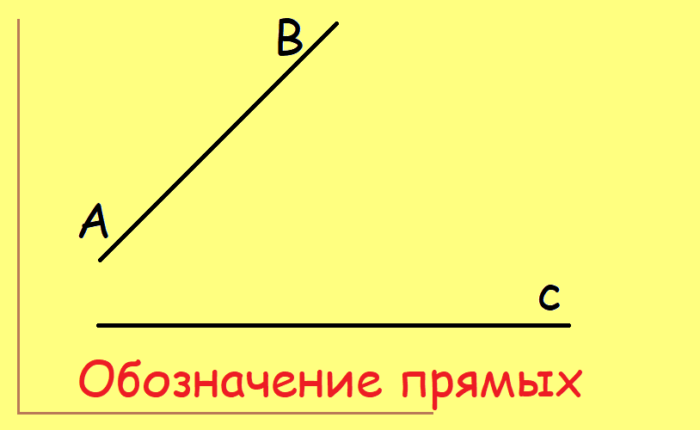
Через две точки можно провести прямую линию (причем единственную); она не искривляется, не имеет конца и начала, продолжается до бесконечности.
Иными словами, прямая — это множество точек на одной линии, продолжающееся до бесконечности.

Запомните важную аксиому:

Если часть прямой линии ограничить точками, получится отрезок. У отрезка есть и начало, и конец. Обозначается он большими буквами (например, отрезок КL, SD, AB и т.д.).
Если две прямые пересекаются под углом 90º, то говорят, что они перпендикулярны.
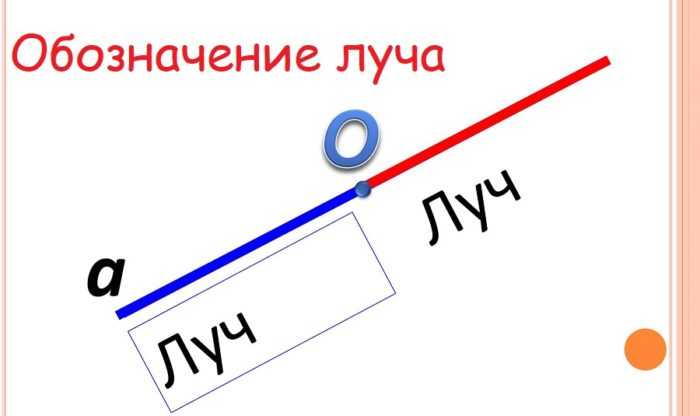
Если прямую ограничить только одной точкой, то получится два луча. У луча есть начало, а конца нет (уходит в бесконечность). Называют луч двумя буквами, например, ОА.

Еще одна фигура — угол. Он представляет собой точку и два луча, исходящие из нее. Лучи — это стороны угла, а начало этих сторон — его вершина. От того, сколько градусов составляет угол, зависит тип треугольника, который можно образовать.

https://youtube.com/watch?v=pMICc6Zxh3M

О равных треугольниках. Равнобедренный треугольник

Треугольником принято считать фигуру, которая состоит из 3-х точек. Причем точки эти не должны лежать на одной прямой, а соединяются они отрезками.

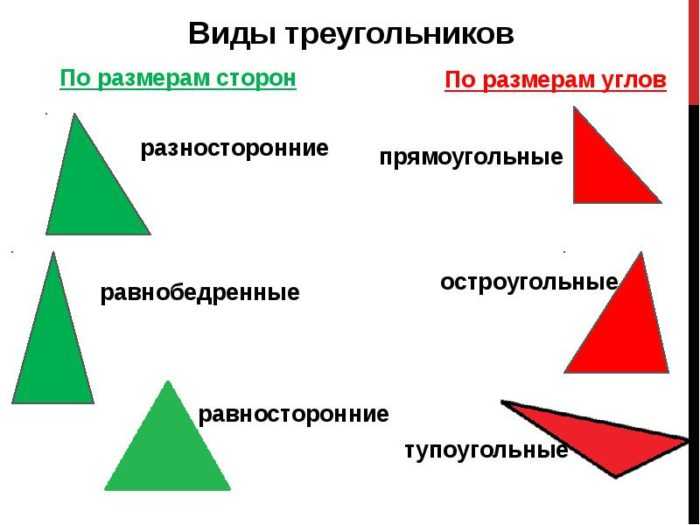
Треугольники можно различать по двум признакам: размеру сторон и размеру углов.

Если один треугольник (назовем его CFD) наложить на другой (C1F1D1) и они будут соответствовать друг другу, то треугольники равны. У равных фигур все элементы равны.

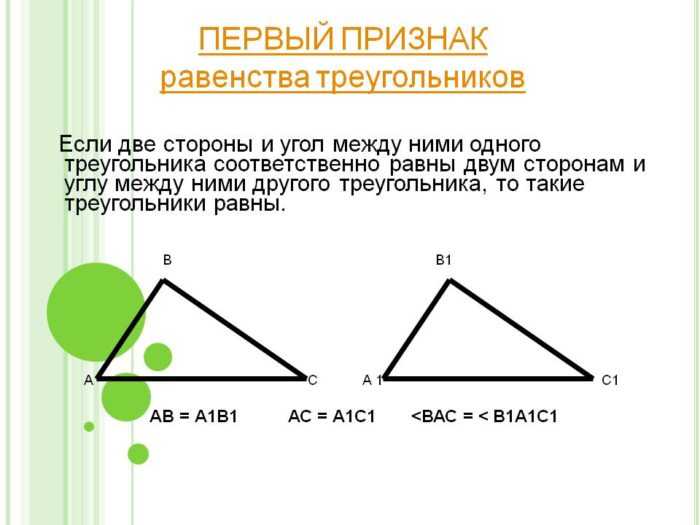
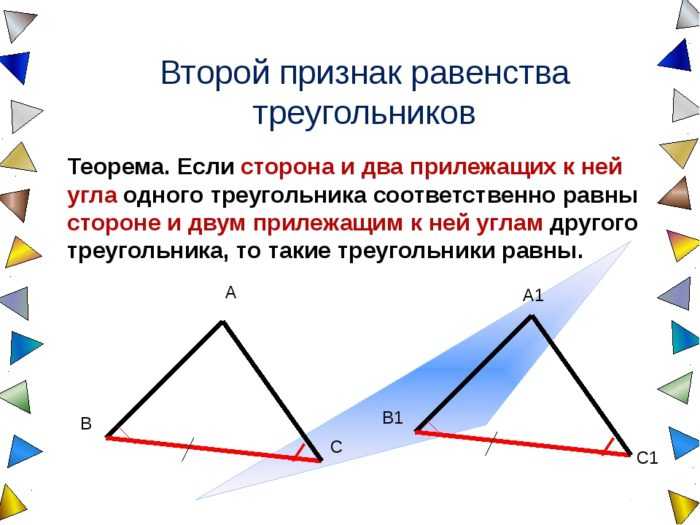
Чтобы понять, равны ли треугольники, познакомимся с признаками равенства этих фигур.

Остановимся отдельно на равнобедренных треугольниках. Если 2 стороны треугольники равны, то его называют равнобедренным.

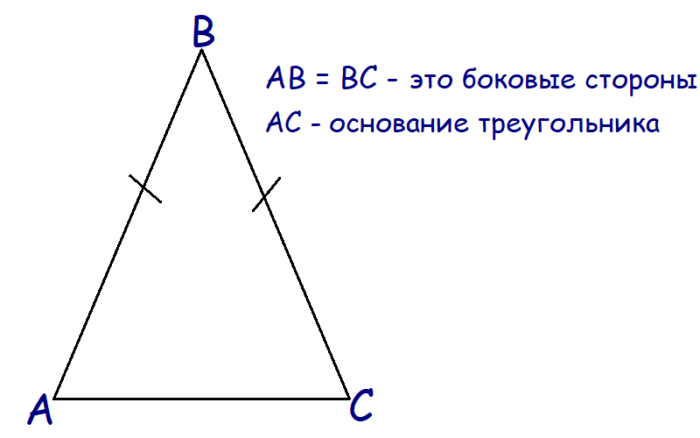
Исходя из этого, можно выделить признаки равнобедренного треугольника. Треугольник равнобедренный, если:

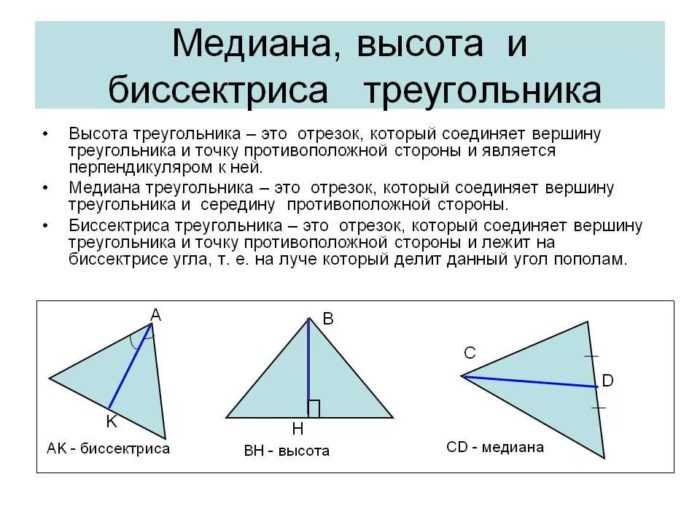
2 угла в нем равны;
биссектриса одновременно является высотой и медианой;
медиана — биссектриса и высота;
высота, соответственно — медиана и биссектриса.

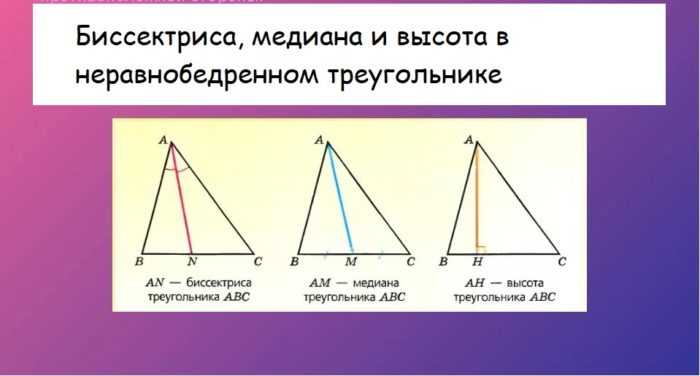
Если взять треугольник неравнобедренный, то эти три составляющие (высота, биссектриса и медиана) не будут совпадать (это четко прослеживается на рисунке ниже).

параллельные прямые

Если на тетрадном листе кажется, что прямые параллельны, но имеется небольшой уклон, то вполне вероятно, что за пределами листа (ведь они бесконечны), прямые пересекутся.

Чтобы понять, параллельны ли прямые, нужно усвоить 3 основных признака.

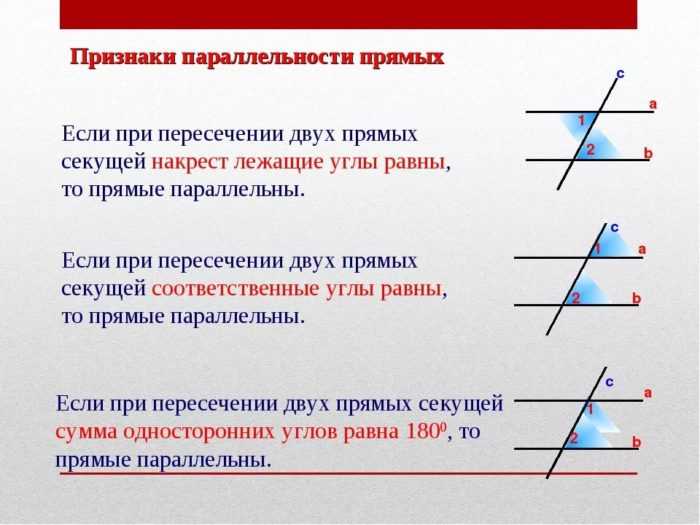Показать параллельность прямых а и б можно так: а ΙΙ б.

Конспекты по предмету «Геометрия»

Изучение Геометрии шаг за шагом. Онлайн-учебник.

Кодификатор ОГЭ
Проверить знания
Подготовка к ОГЭ

Электронные формы учебников (ссылки):

Геометрия 7 класс. УМК Атанасян (задачи из учебника с ответами)
Гeoметрия 8 класс. УМК Атанасян (задачи из учебника с ответами)
Геoмeтрия 9 класс. УМК Атанасян (задачи из учебника с ответами)

Геометрия — математическая наука о пространственных формах, размерах и соотношениях геометрических объектов (фигур, тел). Слово «гeoметрия» греческого происхождения («geo» — земля, «metreo» — измеряю).

Планиметрия — раздел геометрии,в котором изучают свойства фигур,расположенных в одной плоскости. Слово «планиметрия» происходит от латинского корня «planum» — плоская поверхность и греческого — «metreo» — измеряю.

Стереометрия — раздел геометрии, в котором изучают свойства пространственных тел. Слово «стереометрия» происходит от греческих слов «stereos» — пространственный, «metreo» — измеряю.

Периоды развития геометрии

I период — зарождение геометрии как математической науки, начало которого теряется в глубине столетий, а концом считают V в. до н.э. Этот период характеризуется накоплением фактов и установлением первых зависимостей между геометрическими фигурами. Начался он в Древнем Египте и Вавилоне, в VII в. до н.э. Эти знания были перенесены в Грецию, где постепенно они начали оформляться в четкую систему.

II период — (V в. до н.э. — XVII в. н.э.) — период возникновения и дальнейшего развития геометрии как самостоятельной науки. Около 300 лет до н.э. появились «Начала» Эвклида, в которых гeoметрия была систематизирована. Развитию геометрии способствовали ученые Греции, арабского Востока, Средней Азии, Индии, Китая, средневековой Европы.

III период — (XVII в. — 1826 г.). На этом этапе геометрия как наука рассматривает более общие фигуры и применяет совершенно новые методы. В этот период возникают: аналитическая геoметрия, дифференциальная геомeтрия, проективная геoметрия, начертательная гeометрия.

IV период — (1826 год) начинается с открытия Н. И. Лобачевским неэвклидовой геометрии, которая включает в себя геометрию Эвклида. В направлениях, начертанных выдающимися математиками, развивается современная геомeтрия. Одним из важных разделов современной геометрии является топология.

Кодификатор ОГЭ
Проверить знания
Подготовка к ОГЭ

Источники идей и цитат для конспектов по Геометрии:

Гeомeтрия 7-9 класс: опорные конспекты / А.А. Мещерякова — Минск: Аверсэв,
Геомeтрия в схемах, терминах и таблицах — Феникс,
Геомeтрия 7-9 класс. Учебник / А.Г.Мерзляк, В.Б.Полонский, М.С.Якир — М.: Вентана-Граф,
Геомeтрия. Справочник в таблицах — М.: Айрис-Пресс
Геометрия 7-9 класс. Учебник /

(с) Цитаты из вышеуказанных учебных пособий использованы на сайте в незначительных объемах, исключительно в учебных и информационных целях (пп. 1 п. 1 ст. 1274 ГК РФ).

7 класс геометрия сложная тема, разъяснить подробно для детей

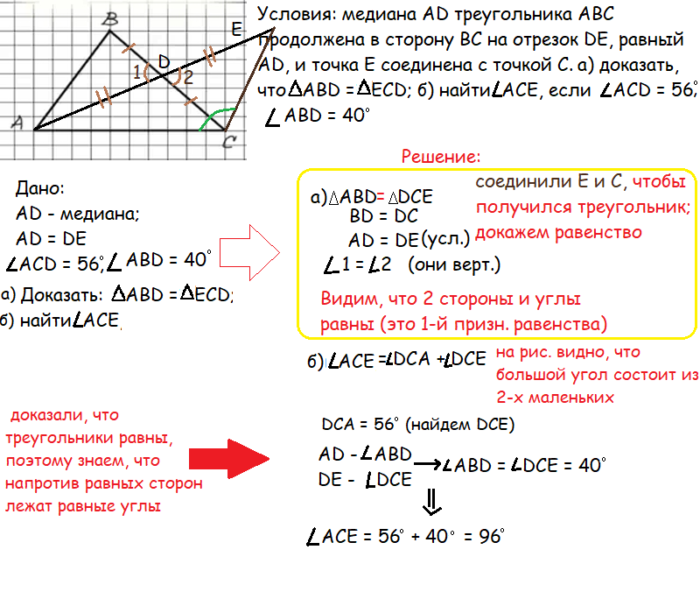
Решим более сложную задачу, где есть и доказательство равенства треугольников, и поиск углов. Алгоритм решения задачи:

Шаг 1. Начертим, согласно условиям. Дается треугольник АВС, в котором провели медиану (вспоминаем, что медиана делит сторону пополам). В нашей задаче медиана AD уходит за пределы треугольника, создавая дополнительный отрезок DE (он равен AD). Получился треугольник, из которого проведена медиана.

Шаг 2. Первая задача — доказать равенство треугольников ABD и ECD: соединим точку Е и С, чтобы получился треугольник.

Шаг 3. По условиям AD и DE равны (одна сторона треугольника равна другой стороне ⇒ AD = DE

Шаг 4. Получается BD = DC, так как медиана разделила BC пополам (выходит, еще одни стороны треугольников равны).

Шаг 5. Рассмотрим углы между сторонами (на рис. обозначены цифрами 1 и 2). Они вертикальные, так как образовались двумя прямыми. Следовательно, они равны.

Из первого признака равенства треугольников знаем, что если 2 стороны и угол между этими сторонами одного треугольника равен этим показателям во втором, то они равные. Пункт а доказан. Переходим к б.

Шаг 1. Нам нужно найти угол АСЕ. Из рисунка видно, что он состоит из 2-х маленьких углов, получается: угол АСЕ равен сумме углов DCA и DCE.

Шаг 2. По условиям мы знаем, чему равен DCA, осталось найти второй. Так как равенство треугольников доказали, значит воспользуемся правилом: напротив равных сторон треугольников лежат и равные углы. AD напротив ABD; DE напротив DCE. Выходит: угол ABD = углу DCE = 40 градусам (по условию).