Введение
Индексы позволяют измерять
изменения сложных явлений. Например,
требуется определить, насколько
увеличился (или уменьшился) в данном
году по сравнению с прошлым годом
физический объем всей продукции
предприятия. Ясно, что продукция
разного качества и вида не поддается
непосредственному суммированию. Для
характеристики изменения таких сложных
явлений во времени применяются индексы
динамики.
При помощи индексов можно
характеризовать изменение во времени
самых различных показателей.
Индексы являются показателями
сравнений не только с прошлым
периодом, но и с другой территорией,
а также с нормами, прогнозами,
планами и т.д.
Индексный метод позволяет
решить множество задач, при этом упрощаются
вычисления и экономится время на произведение
данных расчетов.
Средние индексы
В зависимости от методологии расчета индивидуальных и сводных индексов различают средние арифметические и средние гармонические индексы. Другими словами, общий индекс, построенный на базе индивидуального индекса, принимает форму среднего арифметического или гармонического индекса, т. е. он может быть преобразован в средний арифметический и средний гармонический индексы.
Идея построения сводного индекса в виде средней величины из индивидуальных (групповых) индексов вполне объяснима: ведь сводный индекс является общей мерой, характеризующей среднюю величину изменения индексируемого показателя, и, конечно, его величина должна зависеть от величин индивидуальных индексов. А критерием правильности построения сводного индекса в форме средней величины (среднего индекса) является его тождественность агрегатному индексу.
Преобразование агрегатного индекса в средний из индивидуальных (групповых) индексов производится следующим образом: либо в числителе, либо в знаменателе агрегатного индекса индексируемый показатель заменяется его выражением через соответствующий индивидуальный индекс. Если такую замену сделать в числителе, то агрегатный индекс будет преобразован в средний арифметический, если же в знаменателе – то в средний гармонический из индивидуальных индексов.
Например, известен индивидуальный индекс физического объема iq = q1/q0 и стоимость продукции каждого вида в базисном периоде (q0p0). Исходной базой построения среднего из индивидуальных индексов служит сводный индекс физического объема:
(агрегатная форма индекса Ласпейреса).
Из имеющихся данных непосредственно суммированием можно получить только знаменатель формулы. Числитель же может быть получен перемножением стоимости отдельного вида продукции базисного периода на индивидуальный индекс:
Тогда формула сводного индекса примет вид:
т. е. получим средний арифметический индекс физического объема, где весами служит стоимость отдельных видов продукции в базисном периоде.
Допустим, что в наличии имеется информация о динамике объема выпуска каждого вида продукции (q) и стоимости каждого вида продукции в отчетном периоде (p1q1). Для определения общего изменения выпуска продукции предприятия в этом случае удобно воспользоваться формулой Пааше:
Числитель формулы можно получить суммированием величин q1P1, а знаменатель – делением фактической стоимости каждого вида продукции на соответствующий индивидуальный индекс физического объема продукции, т. е. делением: p1q1/iq, тогда:
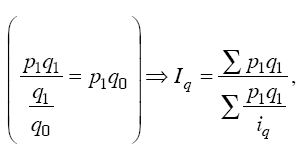
таким образом, получаем формулу среднего взвешенного гармонического индекса физического объема.
Применение той или иной формулы индекса физического объема (агрегатного, среднего арифметического и среднего гармонического) зависит от имеющейся в распоряжении информации. Также нужно иметь в виду, что агрегатный индекс может быть преобразован и рассчитан как средний из индивидуальных индексов только при совпадении перечня видов продукции или товаров (их ассортимента) в отчетном и базисном периодах, т. е. когда агрегатный индекс построен по сравнимому кругу единиц (агрегатные индексы качественных показателей и агрегатные индексы объемных показателей при условии сравнимого ассортимента).
показать содержание
Ряды агрегатных индексов с постоянными и переменными весами
При изучении динамики экономических явлений строятся и исчисляются индексы за ряд последовательных периодов. Они образуют ряды либо базисных, либо цепных индексов. В ряду базисных индексов сравнение индексируемого показателя в каждом индексе производится с уровнем одного и того же периода, а в ряду цепных индексов индексируемый показатель сопоставляется с уровнем предыдущего периода.
В каждом отдельном индексе веса в его числителе и знаменателе обязательно фиксируются на одном и том же уровне. Если же строится ряд индексов, то веса в нем могут быть либо постоянными для всех индексов ряда, либо переменными.
Ряд базисных индексов объема продукции Σq1p0/Σq0p0,Σq2p0/Σq0p0,Σq3p0/Σq0p0 и т. д. имеет постоянные веса (р0). Постоянные веса (р0) имеет и ряд цепных индексов: Σq1p0/Σq0p0,Σq2p0/Σq1p0,Σq3p0/Σq2p0 и т. д.
Ряд цепных индексов цен Σp1q1/Σp1q0,Σp2q2/Σp2q0, Σp3q3 /Σp3q2 и т. д. построен с переменными весами (в 1-м индексе – q1 во 2-м – q2 и т. д.).
Для индексов динамики с постоянными весами имеет силу взаимосвязь между цепными и базисными темпами роста (индексами):
Таким образом, использование постоянных весов в течение ряда лет позволяет переходить от цепных индексов к базисным, и наоборот. Поэтому ряды индексов объема продукции и объема проданных товаров строятся в статистической практике с постоянными весами. Так, в индексах объема продукции в качестве постоянных весов используются цены, зафиксированные на уровне, который был установлен на 1 января какого-либо базисного года. Такие цены, используемые в течение ряда лет, называются сопоставимыми (фиксированными).
Использование в индексах объема продукции (товаров) сопоставимых цен позволяет путем простого суммирования получать итоги за несколько лет. Сопоставимые цены не должны сильно отличаться от действующих (текущих) цен, поэтому их периодически пересматривают, переходя к новым сопоставимым ценам. Чтобы иметь возможность исчислять индексы объема продукции за длительные периоды, в течение которых применялись различные сопоставимые цены, продукцию одного года оценивают как в прежних, так и в новых фиксированных ценах. Индекс за длительный период исчисляют цепным методом, т. е. путем перемножения индексов за отдельные отрезки этого периода.
Ряды индексов качественных показателей, которые экономически правильно взвешивать по весам текущего периода, строятся с переменными весами.
Роль индексов в изучении социально-экономических явлений
Индексный метод анализа
является одним из основных методов
статистического изучения социально-экономических
явлений. Индексы в статистической
практике наряду со средними величинами
— наиболее часто встречающиеся показатели.
Они используются для изучения развития
различных явлений и процессов
как на народнохозяйственном отраслевом
уровнях, так и на уровне предприятий и
их подразделений. С помощью индексов
осуществляется сопоставление показателей
во времени и в пространстве.
Главной отличительной чертой индексов
от обычных относительных величин является
то, что сопоставляемые показатели обычно
характеризуют явления, состоящие из разнородных
элементов, непосредственное суммирование
которых невозможно в силу их несоизмеримости.
Система взаимосвязанных
индексов дает возможность широко применять
индексный метод для изучения
взаимосвязей общественных явлений, проведения
факторного анализа с целью определения
роли отдельных факторов (не зависимых
друг от друга) на изменение сложного
явления.
В отечественной статистике
принята следующая практика факторного
анализа: если результативный показатель
можно представить как произведение
объемного и качественного факторов,
то, определяется влияние объемного
фактора на изменение результативного
показателя, качественный фактор фиксируют
на уровне базисного периода; если же
определяется влияние качественного
показателя, то объемный фактор фиксируется
на уровне отчетного периода.
По существу, любой агрегатный
индекс построен по такому принципу обособленного
рассмотрения влияния отдельных
факторов на изменение сложного показателя.
Список использованной литературы
- Статистика: национальные счета, показатели и методы анализа: Справ, пособие / Под ред. И.Е. Теслюка. — Минск: БГЭУ, 1995. — С.332-338.
- Торвей Р. Индексы потребительских цен: методологическое руководство // Международная организация труда: Пер. с англ. — М.: Финансы и статистика, 1993. — 248 с.
- Уотшем Т.Дж, Паррамоу К. Количественные методы в финансах: Учеб. пособие для вузов / Пер. с англ, под ред. М.Р. Ефимовой. — М.: Финансы, ЮНИТИ, 1999.-С.5-128.
- Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А. Практикум по теории статистики. под ред. профессора Р.А. Шмойловой. – М.: Финансы и статистика, 2004 – с 300 — 316.
Агрегатные индексы объемных показателей
Объемные показатели могут быть соизмеримыми (Т, рQ, zQ) и несоизмеримыми (объем продукции или товаров разного вида – Q). Соизмеримые объемные показатели могут непосредственно суммироваться, и построение агрегатных индексов не вызывает трудностей.
Для получения общего итога и построения агрегатного индекса несоизмеримого объемного показателя нужно предварительно соизмерить отдельные значения этого показателя. Исходя из экономической сущности явления, нужно найти общую меру и использовать ее в качестве коэффициента соизмерения. Такой общей мерой для объемных показателей являются связанные с ними качественные показатели. Так, объемы различных видов продукции могут быть соизмерены с помощью цены (р), себестоимости (z) и трудоемкости (t) этих продуктов. Умножая индексируемый объемный показатель на тот или иной качественный показатель, не только обеспечивается возможность суммирования, но одновременно учитывается также роль каждого элемента, например продукта, в реальном экономическом процессе, т. е. его статистический вес в этом процессе.
Поскольку в индексе объемного показателя в качестве весов могут выступать различные качественные показатели, возникает вопрос о том, какой же именно их них следует использовать. Этот вопрос в каждом конкретном случае должен решаться в соответствии с той познавательной экономической задачей, которая ставится перед индексом, т. е. выбор тех или иных весов-соизмерителей должен быть обоснован экономически.
В практике экономической и статистической работы в качестве весов агрегатного индекса объема продукции обычно используются цены. Так строятся индексы объема промышленной и сельскохозяйственной продукции, а также индексы физического объема товарооборота.
В ряде случаев изменение объема продукции интересует не само по себе, а с точки зрения его влияния на изменение показателя более сложного порядка: общей стоимости продукции, общей ее себестоимости, общих затрат рабочего времени, общего объема производства на данном его участке и т. п. В таких случаях выбор весов-соизмерителей определяется взаимосвязью показателей-факторов, от которых зависит более сложный показатель.
Чтобы индекс отражал только изменение индексируемого объемного показателя, веса в его числителе и знаменателе фиксируются на уровне одного и того же периода. В практике экономической работы в индексах динамики объемных показателей веса обычно фиксируются на уровне базисного периода (см. формулу 7.2). Это обеспечивает возможность построения систем взаимосвязанных индексов.
Для индивидуальных объемных показателей (объем реализации, объем производительности продукции, посевная площадь) веса выбираются на уровне базисного периода. Например:
где In– сводный индекс урожайности; I – сводный индекс стоимости товарооборота; Iq – сводный индекс себестоимости.
В отличие от индексов качественных показателей, которые исчисляются по сравнимому кругу единиц (сравнимой продукции), сводные индексы объемных показателей в целях полноты и точности должны охватывать весь круг единиц, произведенных (или проданных) в каждом периоде. В связи с этим возникает вопрос о том, какие значения весов следует брать для тех видов продукции, которые в одном из сравниваемых периодов не производились.
В практике статистики в таких случаях применяются два способа. При расчете индексов объема промышленной продукции новые ее виды, для которых нет цен базисного периода, оцениваются условно по ценам текущего периода. При расчете же индексов объема проданных товаров используется метод, основанный на условном предположении, что и цены на новые товары изменились в той же степени, что цены на сравниваемый круг аналогичных товаров.
Понятие и виды индексов
Индекс (лат. index) — это
относительная величина, показывающая,
во сколько раз уровень изучаемого
явления в данных условиях отличается
от уровня того же явления в других
условиях.
В статистике под индексом
понимается относительный показатель,
который выражает соотношение величин
какого-либо явления во времени, в
пространстве, или сравнение фактических
данных с любым эталоном.
По степени охвата явления
различают индексы индивидуальные
(элементарные) и сводные (сложные),
которые, в свою очередь, делятся
на общие и групповые.
Индивидуальные индексы
служат для характеристики изменения
отдельных элементов сложного явления.
Например, изменение объема производства
отдельных видов продукции (телевизоров,
электроэнергии и т.д.), а также
цен на акции какого-либо предприятия.
Сводные (сложные) индексы
служат для измерения сложного явления,
составные части которого непосредственно
несоизмеримы. Например, изменения
физического объема продукции, включающей
разноименные товары, индекса цен
акций предприятий региона и
т.п.
Индивидуальные индексы:
индекс цен:
индекс физического объема продукции:
индекс трудоемкости:
Сводные индексы:
1) Если сравним товарооборот в
текущем периоде с его величиной
в базисном периоде, то получим сводный индекс товарооборота:
2) Для того, чтобы измерить только
влияние цен необходимо зафиксировать
количество проданных товаров,
т.о. получаем сводный индекс цен:
3) Для измерения влияния изменения количества
проданных товаров используют сводный индекс физического
объема реализации:
Между рассчитанными индексами
существует взаимосвязь: Ip* Iq = Ipq.
Индексы классифицируются по
трем признакам:
– по содержанию изучаемых
объектов;
– по степени охвата элементов
совокупности;
– по методам расчета общих
индексов.
По содержанию изучаемых
величин индексы разделяют на
индексы количественных (объемных)
и индексы качественных показателей.
Индексы количественных
показателей – индексы физического объема
промышленной и сельскохозяйственной
продукции, физического объема розничного
товарооборота, национального дохода,
потребления продаж иностранной валюты
и др. Все индексируемые показатели этих
индексов являются объемными, поскольку
они характеризуют общий, суммарный размер
(объем) того или иного явления и выражаются
абсолютными величинами. При расчете таких
индексов количества оцениваются в одинаковых,
сопоставимых ценах.
Индексы качественных
показателей – индексы курса валюты, цен,
себестоимости, производительности труда,
заработной платы, урожайности и т.д. Индексируемые
показатели этих индексов характеризуют
уровень явления в расчете на ту или иную
единицу совокупности: цена за единицу
продукции себестоимость единицы продукции
и т.д. Такие показатели называются качественными.
Они носят расчетный, вторичный характер.
Качественные показатели измеряют не
общий объем, а интенсивность и эффективность
явления или процесса. Как правило, они
являются либо средними, либо относительными
величинами. Расчет таких индексов производится
на базе одинаковых, неизменных количеств
продукции.
По степени охвата единиц
совокупности индексы делятся на
два класса: индивидуальные и общие.
Индивидуальные
индексы служат для характеристики
изменения удельных элементов сложного
явления.
Общий индекс отражает изменение всех элементов
сложного явления. При этом под сложным
явлением понимают такую статистическую
совокупность, отдельные элементы которой
непосредственно не подлежат суммированию.
Если индексы охватывают
не все элементы сложного явления, а
лишь часть, то их называют групповыми
или субиндексами.
Заключение
В течение уже многих лет
индексами пользуются и для аналитических
целей. Так, допустим, с помощью индексов
устанавливают, в какой мере общее
изменение среднего заработка работников
промышленности зависит от изменения
уровня заработка в каждой отрасли
промышленности, а в какой мере
— от изменения соотношения численности
работников отдельных отраслей (более
подробно мы рассмотрим это в дальнейшем).
Такое применение индексов
приводит к рассмотрению их как аналитических
показателей. Обычно вычисляемый по
формуле Пааше индекс цен рассматривается
также как показатель аналитический,
выражающий влияние изменения цен
на изменение общей стоимости
продукции; вторым, связанным с ним
индексом, является индекс объема реализованных
товаров.
Всякий индекс, в статистике,
есть относительный показатель, характеризующий
изменение социально-экономического явления
во взаимосвязи с другим (или другими)
явлением, абсолютная величина которого
предполагается при этом неизменной.
Следовательно:
1) индекс — величина
относительная, вследствие чего
мы абстрагируемся от абсолютного
размера явления;
2) индекс выражает изменение
одного явления во взаимосвязи
с другим (другими), от изменений
которого мы при этом абстрагируемся,
предполагая его величину неизменной;
3) в индексе всегда
есть элемент условности.
Что же касается международной
статистики, в частности, сопоставления
количественных показателей ресурсного
обеспечения науки современной
России и зарубежных стран, то особых
трудностей здесь нет, т.к. реорганизация
принципов статистического учета
позволила преодолеть существовавшую
в СССР проблему принципиальной несопоставимости
большинства показателей. К настоящему
времени в российской статистике
состояния науки по сравнению
с зарубежной остаются различия только
в детальности, периодичности, полноте
охвата и доступности разнообразных
статистических данных.




























