Классификация методов разделения
В предлагаемой статье предпринята очередная попытка создать общую классификацию методов разделения. По единым классификационным признакам, которыми служат фазовые превращения и межфазный перенос, все методы разделения гомогенных смесей веществ делятся на пять групп: методы, основанные на образовании выделяемыми веществами новых фаз; методы, основанные на различиях в межфазном распределении, с выделением в отдельную группу хроматографических методов; мембранные методы, основанные на индуцированном переносе веществ из одной фазы в другую через разделяющую их третью фазу; методы разделения в пределах одной фазы, основанные на различиях в скоростях и направлениях пространственного перемещения частиц разделяемых веществ в пределах одной флюидной фазы под действием различных полей; комбинированные методы, основанные на различных сочетаниях признаков предыдущих групп. Описания каждой группы методов включают их внутригрупповую классификацию и сведения о наиболее важных и наименее известных …
Метод k ближайших соседей
Метод k ближайших соседей (k-NN) является одним из наиболее простых алгоритмов классификации. Он основан на идее о том, что объекты, близкие друг к другу по некоторым признакам, скорее всего принадлежат к одному классу.
Алгоритм k-NN определяет класс нового объекта, основываясь на классах k ближайших к нему объектов из обучающей выборки. При этом выбор метрики расстояния, используемой для определения близости объектов, играет важную роль в качестве классификации.
Одним из преимуществ метода k-NN является его простота в реализации и понимании. Кроме того, он хорошо справляется с классификацией нелинейных объектов и устойчив к шуму в данных. Однако, он может быть неэффективен при большом объеме выборки, так как требует хранения всей обучающей выборки.
Примером использования метода k-NN может быть классификация пациентов на основе их медицинских данных для выявления риска заболеваний. Также метод k-NN может использоваться в компьютерном зрении для распознавания образов и сравнения изображений.
- Преимущества: простота в реализации и понимании, устойчивость к шуму и эффективность при классификации нелинейных объектов.
- Недостатки: неэффективен при больших объемах выборки, зависимость от выбора метрики расстояния.
- Пример использования: классификация пациентов на основе медицинских данных, распознавание образов в компьютерном зрении.
Еще термины по предмету «Конфликтология»
Анннулирование
форма психологической защиты, представляющая собой поведение или мысли, способствующие символическому сведению на нет предыдущих акта или мысли, вызвавших сильное беспокойство, чувство вины. Правило А. — «отмени это».
Дефавортизация
один из эффектов социальной перцепции, состоящий в позитивном восприятии оппонента представителями противоположной стороны. Индикаторы Д.: представления, оценочные суждения, эмоциональные реакции. Пример Д. – представление рядом российских СМИ в положительном плане агрессивных действий чеченской стороны в ходе двух чеченских конфликтов в 90-е гг. прошлого века.
Утечка мозгов
отъезд интеллектуалов и квалифицированных специалистов из одной страны в другую. Конфликтоген.
-
Иерархические методы классификации
-
Иерархический метод классификации
-
Метод иерархической классификации
-
Методом фасетной классификации
-
Фасетный метод классификации
-
Классификация
-
Заводская классификация
-
Классификация игр
-
Классификация проектов
-
Классификация Кеппена
-
Классификация земель
-
Классификация землепользования
-
Классификация почв
-
Классификация карт
-
Классификация предметов
-
Классификация деревьев
-
Классификация в статистике
-
Классификация проблем
-
Классификация продуктов
-
Классификация целей
3 метода классификации информации
Существует три вида систем классификации информации: иерархическая, фасетная и дескрипторная. Отличаются они тем, что в них по-разному используются классификационные параметры.
Иерархическая система
Отличительные черты:
- Строгая структурированность (количество классификационных признаков имеет большое значение).
- Объект на любом из уровней может быть причислен лишь к одному классу.
- Для распределения по группам на каждом из следующих уровней необходимо иметь информацию о классификационных признаках (соответствующих данному уровню) и их толкованиях.
- Глубина классификации определяется количеством определенных для нее уровней.
Узнай, какие ИТ — профессии входят в ТОП-30 с доходом от 210 000 ₽/мес
Команда GeekBrains совместно с международными специалистами по развитию карьеры
подготовили материалы, которые помогут вам начать путь к профессии мечты.
Подборка содержит только самые востребованные и высокооплачиваемые специальности и направления в
IT-сфере. 86% наших учеников с помощью данных материалов определились с карьерной целью на ближайшее
будущее!
Скачивайте и используйте уже сегодня:

Александр Сагун
Исполнительный директор Geekbrains
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда
Подборка 50+ ресурсов об IT-сфере
Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT
ТОП 50+ сервисов и приложений от Geekbrains
Безопасные и надежные программы для работы в наши дни
Получить подборку бесплатно
pdf 3,7mb
doc 1,7mb
Уже скачали 21876
Преимущества:
- Метод прост.
- Большой плюс в том, что на разных ступенях иерархии в структуре задействуются независимые классификационные признаки.
Отрицательные моменты:
- Структура достаточно жёсткая.
- Если объект обладает признаками, которые заранее не были предусмотрены, то его невозможно будет отнести ни к одной из групп.
Фасетная система классификации информации
«Facet» в переводе с английского – «рамка».
Тут можно определять никак не связанные между собой признаки классификации и отталкиваться от их семантики. Фасеты – это и есть критерии классификации.
| Фасет 1 | Фасет 2 | Фасет 3 | Фасет 4 |
| … | … | … | … |
Отличительные черты:
- В процессе каждый из классифицируемых объектов наделяется определенным значением из фасета. Какие-то из рамок могут остаться неиспользованными.
- Каждый объект причисляется к конкретной группировке.
- В созданной системе этого вида значения рамок не должны повторяться.
- Каждый из фасетов в любой момент можно видоизменять, тем самым преобразовав и систему в целом.

Фасетная система классификации информации
Преимущества:
- Внедрение большого числа характеристик для классификации.
- Возможность преобразования всей системы с сохранением структуры созданных групп.
Отрицательные моменты:
Систему довольно трудно выстраивать из-за большого числа критериев классификации.
Дескрипторная система
Применяется в случаях, когда классификация объектов осуществляется на естественном языке. Например, в библиотечном деле.
Суть процесса:
- Собираются слова или словосочетания (в том числе синонимы), подходящие для описания конкретной области.
- Далее в отношении этих слов выполняется нормализация, то есть, выявляется одно или несколько самых часто используемых.
- Таким образом собирается словарь дескрипторов.
Для того чтобы собирать информацию по более широким областям, между дескрипторами специально выискиваются связи, которые могут быть следующих трех типов:
- синонимические (студент – ученик – обучающийся);
- родовидовые (университет – факультет – кафедра);
- ассоциативные (слушатель – учеба – аудитория – занятие).
Алгоритм случайного леса
Случайный лес (Random Forest) — это один из самых популярных алгоритмов машинного обучения для задач классификации и регрессии. Это тип ансамбльных методов, который основан на использовании нескольких деревьев решений, объединенных в единый алгоритм.
Для обучения случайного леса необходимо подготовить набор данных из признаков и целевых переменных. Затем случайным образом выбираются примеры из этих данных, и на каждом таком наборе строится отдельное дерево решений.
При построении каждого дерева выбираются случайные признаки из набора, на основе которых будет производиться разбиение данных на две части. Затем выбирается наилучший признак и соответствующее значение для разделения данных. Процесс разбиения выполняется до тех пор, пока все листья дерева не будут соответствовать данным только одного класса.
Итоговый результат получается путем проведения голосования или усреднения результатов отдельных деревьев. Случайный лес показывает высокую точность классификации на разнообразных данных, а также обладает устойчивостью к переобучению и выбросам в данных.
Примеры использования алгоритма случайного леса включают в себя классификацию текстовых данных, распознавание образов и наблюдений в биологии, прогнозирование кликов на рекламные объявления и рейтинги кредитоспособности.
Машины опорных векторов
Машины опорных векторов (SVM) — это мощный алгоритм для классификации и регрессии, который использует метод опорных векторов для построения оптимальной гиперплоскости, разделяющей объекты разных классов. Эти алгоритмы считаются одними из наиболее точных и надежных в методах машинного обучения.
Работа SVM состоит в том, чтобы найти оптимальную гиперплоскость, которая максимально разделяет объекты разных классов. Для этого SVM использует метод опорных векторов: выбирает такую гиперплоскость, которая максимально удалена от объектов наиболее близких к ней.
Применение SVM может быть очень полезным в различных областях, таких как прогнозирование цен на акции, обнаружение мошеннических операций в финансовых транзакциях, классификация изображений и текстов, анализ генетических и клинических данных и т.д.
Хотя SVM являются мощным инструментом машинного обучения, они могут быть сложными для понимания и реализации. Для их применения необходимо иметь некоторые знания в области математики и программирования, а также более подробно изучить основные принципы работы SVM и их применения в конкретных задачах машинного обучения.
- Преимущества SVM:
- Высокая точность;
- Хорошая устойчивость к шумам и переобучению;
- Широкий спектр применений в различных областях;
- Эффективная работа в условиях высокой размерности данных.
- Недостатки SVM:
- Сложность реализации и понимания;
- Отсутствие подходящего решения для задач, где объекты имеют сложную взаимосвязь;
- Высокое время обучения при большом количестве данных.
Деревья принятий решений
Деревья принятий решений (Decision Trees) — один из наиболее популярных методов машинного обучения для классификации. Этот метод заключается в создании дерева принятия решений, где каждый узел представляет собой вопрос о значении определенного признака, а каждая ветвь — возможный ответ на этот вопрос.
Дерево строится на основе обучающей выборки, где каждый объект имеет известные значения признаков и известную классификацию. Алгоритм построения дерева включает в себя выбор признака, наиболее эффективно разделяющего выборку на классы, и построение поддерева для каждого значения этого признака.
Дерево принятия решений может работать с любыми типами данных и может использоваться как для классификации, так и для регрессии. Примерами использования являются прогнозирование вероятности ухода клиента, диагностика заболеваний и классификация текстов по темам.
Преимущества метода деревьев принятия решений:
- Простота интерпретации полученных правил;
- Высокая эффективность работы с большими объемами данных;
- Устойчивость к шумам в данных.
Недостатки метода деревьев принятия решений:
- Сильная чувствительность к выбросам в данных;
- Проблемы с многомерностью данных, из-за возможности переобучения модели;
- Трудность обработки пропущенных значений в данных.
В целом, метод деревьев принятий решений является эффективным и простым в использовании инструментом машинного обучения для классификации и прогнозирования
Однако, его использование следует проводить с осторожностью, учитывая особенности данных и возможные проблемы метода
Недостатки методов ближайших соседей
Конечно, здесь
сразу виден недостаток такого подхода: что делать, если представителей обоих
классов будет поровну? Какому классу тогда отдать предпочтение? Можно
попробовать взять нечетное число k, тогда для двух классов эта проблема
будет решена. Но, ведь в окрестности может оказаться и три и четыре разных
классов. Поэтому, эта общая проблема существует и не имеет однозначного
решения.
Другим важным
недостатком являются единичные значения весов для ближайших k образов:
То есть, мы не
учитываем расстояния до соседних объектов, только их наличие или отсутствие. А,
наверное, было бы логично оперировать, в том числе, и расстояниями.
Далее, мы с вами
познакомимся с другими метрическими алгоритмами классификации, которые решают
эти проблемы, хотя порождают некоторые другие. В конце концов, универсальных
решений нет.
Типы классификации
Классификация является важным инструментом в науке, технике, медицине и других областях. Существует несколько типов классификации, которые используются в различных областях:
- Бинарная классификация: разделение объектов на две группы на основе некоторого признака или набора признаков. Например, животные могут быть классифицированы на хищников и травоядных.
- Множественная классификация: разделение объектов на более чем две группы на основе различных признаков. Например, в биологии организмы могут быть классифицированы по их характеристикам, таким как форма, размер, функции органов и так далее.
- Линейная классификация: разделение объектов на группы в порядке следования определенного признака. Например, буквы могут быть классифицированы по алфавиту.
- Иерархическая классификация: разделение объектов на группы на основе их сходства и различия. Например, животные могут быть классифицированы в виде дерева, начиная от класса, до отряда, семейства, рода и вида.
Каждый из этих типов классификации может быть использован в различных сферах. Однако, для получения максимальной точности и полноты классификации, необходимо использовать методы, соответствующие данным типу.
Классификация: формальная постановка
Пусть — множество описаний объектов,
— конечное множество номеров (имён, меток) классов.
Существует неизвестная целевая зависимость — отображение
,
значения которой известны только на объектах конечной обучающей выборки
.
Требуется построить алгоритм
,
способный классифицировать произвольный объект
.
Вероятностная постановка задачи
Более общей считается вероятностная постановка задачи.
Предполагается, что множество пар «объект, класс»
является вероятностным пространством
с неизвестной вероятностной мерой .
Имеется конечная обучающая выборка наблюдений
,
сгенерированная согласно вероятностной мере .
Требуется построить алгоритм
,
способный классифицировать произвольный объект
.
Признаковое пространство
Признаком называется отображение
,
где
— множество допустимых значений признака.
Если заданы признаки
,
то вектор
называется признаковым описанием объекта
.
Признаковые описания допустимо отождествлять с самими объектами.
При этом множество
называют признаковым пространством.
В зависимости от множества признаки делятся на следующие типы:
- бинарный признак: ;
- номинальный признак: — конечное множество;
- порядковый признак: — конечное упорядоченное множество;
- количественный признак: — множество действительных чисел.
Часто встречаются прикладные задачи с разнотипными признаками, для их решения подходят далеко не все методы.
Литература
- Айвазян С. А., Бухштабер В. М., Енюков И. С., Мешалкин Л. Д. Прикладная статистика: классификация и снижение размерности. — М.: Финансы и статистика, 1989.
- Вапник В. Н. Восстановление зависимостей по эмпирическим данным. — М.: Наука, 1979.
- Журавлев Ю. И., Рязанов В. В., Сенько О. В. «Распознавание». Математические методы. Программная система. Практические применения. — М.: Фазис, 2006. ISBN 5-7036-0108-8.
- Загоруйко Н. Г. Прикладные методы анализа данных и знаний. — Новосибирск: ИМ СО РАН, 1999. ISBN 5-86134-060-9.
- Шлезингер М., Главач В. Десять лекций по статистическому и структурному распознаванию. — Киев: Наукова думка, 2004. ISBN 966-00-0341-2.
- Hastie T., Tibshirani R., Friedman J. The Elements of Statistical Learning. — Springer, 2001. ISBN 0-387-95284-5.
- Mitchell T. Machine Learning. — McGraw-Hill Science/Engineering/Math, 1997. ISBN 0-07-042807-7.
Метрики в пространстве признаков
Давайте начнем с
первого вопроса – способа определения расстояния между двумя любыми векторами в
n-мерном
признаковом пространстве .
Предположим, у нас имеются векторы объектов размеченных данных:
и новые
результаты измерений, которые следует классифицировать:
Тогда, первое,
что приходит в голову, взять евклидовое расстояние между двумя точками:
И такая метрика,
действительно, применяется на практике. Но единственная ли она возможная?
Конечно, нет. В самом простом случае, мы можем обобщить евклидову метрику,
следующим образом:
Здесь —
параметр метрики; —
веса признаков. Такой общий способ вычисления расстояний называется метрикой
Минковского.
Зачем нужны веса
в этой формуле? Дело в том, что признаки могут иметь разный масштаб. Например,
вес золота в граммах и его стоимость в рублях – это два совершенно разных
диапазона значений. Чтобы их в равной степени учитывать при определении
близости векторов, следует нормировать через подбор весовых коэффициентов.
Другой параметр p задает
поведение метрики в разных направлениях. Это проще всего показать на рисунках
эквидистантных кривых:
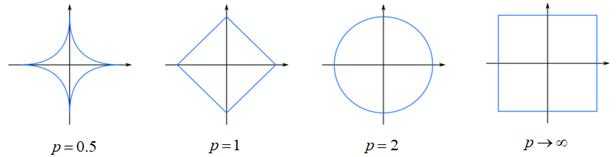
Как видим, при p=1 имеем аналог
суммы разностей модулей координат, при p = 2 –
классическое евклидовое расстояние, а если ,
то круг вырождается в квадрат. Чаще всего на практике можно увидеть метрику с
модулями и квадратами (при p = 1 и 2).
Метод k ближайших соседей (k nearest neighbors, kNN)
Давайте, для
лучшего понимания конкретизируем эту формулу для простейшего случая, когда мы
полагаем:
(помним, что
образы упорядочены по возрастанию расстояний относительно вектора ).
То есть, у нас i-й вес принимает единичное значение для самой
ближайшей точки, и нулевые – для всех остальных:
В этом случае
модель можно записать в виде:
То есть, мы
относим объект к
классу объекта с
минимальным расстоянием в соответствии с выбранной метрикой :
Этот метод
известен под названием метод ближайшего соседа. Очевидно, у него есть
существенный недостаток. Если среди образов одного класса случайно окажется
представитель другого класса, до которого расстояние минимально, то
классификатор сделает неверный вывод:
Побороть такие
единичные выбросы относительно просто, если учитывать не одного, а k ближайших
соседей. В этом случае вектор весов можно определить по правилу:
То есть, теперь
веса будут
принимать единичные значения для первых k ближайших
векторов, а остальные оставаться нулевыми. В результате мы приходим к методу k ближайших
соседей
со следующим алгоритмом классификации:
По простому, мы
предпочтение отдаем тому классу, для которого число из k ближайших
соседей наибольшее:
Например, если в
окрестности объекта семь
образов, причем 4 относятся к классу ,
а 3 – к классу ,
то делаем вывод, что объект принадлежит
первому классу, т.к. его представителей больше.
Примеры прикладных задач
Задачи медицинской диагностики
В роли объектов выступают пациенты.
Признаки характеризуют результаты обследований, симптомы заболевания
и применявшиеся методы лечения.
Примеры бинарных признаков:
пол, наличие головной боли, слабости.
Порядковый признак — тяжесть состояния
(удовлетворительное, средней тяжести, тяжёлое, крайне тяжёлое).
Количественные признаки —
возраст, пульс, артериальное давление,
содержание гемоглобина в крови, доза препарата.
Признаковое описание пациента является, по сути дела,
формализованной историей болезни.
Накопив достаточное количество прецедентов в электронном виде,
можно решать различные задачи:
- классифицировать вид заболевания (дифференциальная диагностика);
- определять наиболее целесообразный способ лечения;
- предсказывать длительность и исход заболевания;
- оценивать риск осложнений;
- находить синдромы — наиболее характерные для данного заболевания совокупности симптомов.
Ценность такого рода систем в том, что они способны мгновенно
анализировать и обобщать огромное количество прецедентов —
возможность, недоступная специалисту-врачу.
Предсказание месторождений полезных ископаемых
Признаками являются данные геологической разведки.
Наличие или отсутствие тех или иных пород на территории района
кодируется бинарными признаками.
Физико-химические свойства этих пород могут описываться
как количественными, так и качественными признаками.
Обучающая выборка составляется из прецедентов двух классов:
районов известных месторождений
и похожих районов, в которых интересующее ископаемое обнаружено не было.
При поиске редких полезных ископаемых
количество объектов может оказаться намного меньше,
чем количество признаков.
В этой ситуации плохо работают классические статистические методы.
Задача решается путём
поиска закономерностей в имеющемся массиве данных.
В процессе решения выделяются короткие наборы признаков,
обладающие наибольшей информативностью —
способностью наилучшим образом разделять классы.
По аналогии с медицинской задачей,
можно сказать, что отыскиваются «синдромы» месторождений.
Это важный побочный результат исследования,
представляющий значительный интерес для геофизиков и геологов.
Оценивание кредитоспособности заёмщиков
Эта задача решается банками при выдаче кредитов.
Потребность в автоматизации процедуры выдачи кредитов впервые возникла
в период бума кредитных карт 60-70-х годов в США и других развитых странах.
Объектами в данном случае являются физические или юридические лица, претендующие на получение кредита.
В случае физических лиц признаковое описание состоит из анкеты,
которую заполняет сам заёмщик, и, возможно, дополнительной информации,
которую банк собирает о нём из собственных источников.
Примеры бинарных признаков: пол, наличие телефона.
Номинальные признаки — место проживания, профессия, работодатель.
Порядковые признаки — образование, занимаемая должность.
Количественные признаки —
сумма кредита, возраст, стаж работы, доход семьи,
размер задолженностей в других банках.
Обучающая выборка составляется из заёмщиков с известной кредитной историей.
В простейшем случае принятие решений
сводится к классификации заёмщиков на два класса:
«хороших» и «плохих».
Кредиты выдаются только заёмщикам первого класса.
В более сложном случае оценивается суммарное число баллов (score) заёмщика,
набранных по совокупности информативных признаков.
Чем выше оценка, тем более надёжным считается заёмщик.
Отсюда и название — кредитный скоринг.
На стадии обучения производится синтез и отбор информативных признаков
и определяется, сколько баллов назначать за каждый признак,
чтобы риск принимаемых решений был минимален.
Следующая задача — решить, на каких условиях выдавать кредит:
определить процентную ставку, срок погашения,
и прочие параметры кредитного договора.
Эта задача также может быть решения методами обучения по прецедентам.
Примеры использования классификации в бизнесе
Классификация может быть полезна в ряде различных бизнес-задач. Например, классификация может использоваться для определения типов потребителей на основе их поведения и предпочтений. Это может помочь компаниям лучше понимать целевую аудиторию и отвечать на ее требования.
Классификация также может быть использована для определения категорий товаров и услуг на основе их основных характеристик, таких как цена, качество и функциональность. Это может помочь компаниям определить, какие продукты или услуги наиболее востребованы и какие следует улучшить или удалить из ассортимента.
Другим примером использования классификации в бизнесе является определение категорий продаж на основе общих характеристик их рентабельности. Это может помочь компаниям лучше понимать, какие продукты предпочитают их клиенты и какие виды продаж могут принести наибольшую прибыль.
- Классификация может быть полезна в ряде различных бизнес-задач
- Классификация может использоваться для определения типов потребителей
- Классификация может быть использована для определения категорий товаров и услуг
- Классификация может помочь определить наиболее востребованные продукты или услуги
- Классификация может помочь лучше понимать, какие продукты предпочитают клиенты и какие виды продаж могут принести наибольшую прибыль
Преимущества метода k ближайших соседей
Несмотря на
очевидные недостатки, метод k ближайших соседей получил широкое
распространение и в ряде задач показывает хорошие результаты. Главным его
преимуществом является простота реализации. Нам достаточно выделить k ближайших
объектов и выделить класс с максимальным числом представителей. Вычислительно,
это очень просто. Здесь даже нет, как такового, алгоритма обучения. Все, что
нам нужно – это иметь массив размеченных данных (представителей классов) и по
ним, затем, относить новые объекты к тому или иному классу. Это называется lazylearning (ленивое
обучение).
Благодаря
простоте реализации, мы можем на обучающей выборке применить технику
скользящего контроля leave-one-out (LOO) для нахождения
наилучшего параметра k. Я напомню, что при LOO мы
последовательно убираем из выборки по одному образу и оцениваем качество его
прогнозирования выбранной моделью (алгоритму классификации) по оставшейся
выборке. Так как наша модель в методе k ближайших соседей зависит от
параметра k:
то его можно подбирать
по методу LOO так, чтобы алгоритм
совершал как можно меньше ошибок:
![]()
Даже для больших
выборок в сотни тысяч и миллион наблюдений можно перебрать целые значения k, скажем в диапазоне
от 1 до 100 и выбрать тот, который даст минимум функции LOO.
Я, надеюсь, из
этого занятия вы поняли, что из себя в целом представляют метрические методы
классификации и как работает алгоритм k ближайших соседей.
Видео по теме
Машинное обучение. Начало
#1. Что такое машинное обучение? Обучающая выборка и признаковое пространство
#2. Постановка задачи машинного обучения
#3. Линейная модель. Понятие переобучения
#4. Способы оценивания степени переобучения моделей
#5. Уравнение гиперплоскости в задачах бинарной классификации
#6. Решение простой задачи бинарной классификации
#7. Функции потерь в задачах линейной бинарной классификации
#8. Стохастический градиентный спуск SGD и алгоритм SAG
#9. Пример использования SGD при бинарной классификации образов
#10. Оптимизаторы градиентных алгоритмов: RMSProp, AdaDelta, Adam, Nadam
#11. L2-регуляризатор. Математическое обоснование и пример работы
#12. L1-регуляризатор. Отличия между L1- и L2-регуляризаторами
#13. Логистическая регрессия. Вероятностный взгляд на машинное обучение
#14. Вероятностный взгляд на L1 и L2-регуляризаторы
#15. Формула Байеса при решении конкретных задач
#16. Байесовский вывод. Наивная байесовская классификация
#17. Гауссовский байесовский классификатор
#18. Линейный дискриминант Фишера
#19. Введение в метод опорных векторов (SVM)
#20. Реализация метода опорных векторов (SVM)
#21. Метод опорных векторов (SVM) с нелинейными ядрами
#22. Вероятностная оценка качества моделей
#23. Показатели precision и recall. F-мера
#24. Метрики качества ранжирования. ROC-кривая
#25. Метод главных компонент (Principal Component Analysis)
#26. Сокращение размерности признакового пространства с помощью PCA
#27. Сингулярное разложение и его связь с PCA
#28. Многоклассовая классификация. Методы one-vs-all и all-vs-all
#29. Метрические методы классификации. Метод k ближайших соседей
#30. Методы парзеновского окна и потенциальных функций
#31. Метрические регрессионные методы. Формула Надарая-Ватсона
#32. Задачи кластеризации. Постановка задачи
#33. Алгоритм кластеризации Ллойда (K-средних, K-means)
#34. Алгоритм кластеризации DBSCAN
#35. Агломеративная иерархическая кластеризация. Дендограмма
#36. Логические методы классификации
#37. Критерии качества для построения решающих деревьев
#38. Построение решающих деревьев жадным алгоритмом ID3
#39. Усечение (prunning) дерева, обработка пропусков и категориальных признаков
#40. Решающие деревья в задачах регрессии. Алгоритм CART
#41. Случайные деревья и случайный лес. Бутстрэп и бэггинг
#42. Введение в бустинг (boosting). Алгоритм AdaBoost при классификации
#43. Алгоритм AdaBoost в задачах регрессии
#44. Градиентный бустинг и стохастический градиентный бустинг
#45. Нейронные сети. Краткое введение в теорию
#46. Обучение нейронной сети. Алгоритм back propagation































