Формула выборки

Основные определения

Понятие выборки используется, когда надо изучить какие-либо свойства совокупности объектов. Свойства объектов можно разделить на качественные и количественные.

Пример 1

Пусть нам необходимо изучить совокупность партии сметаны. Тогда качественным признаком может служить срок её годности, а количественным процент содержания жиров в данной сметане.

Совокупность или выборка может быть разделена на генеральную и выборочную.

Определение 1

Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.

Определение 2

Выборочная совокупность — часть отобранных объектов из генеральной совокупности.

С понятием совокупности также связано понятие объема данной совокупности.

Определение 3

Объем совокупности — число объектов этой совокупности.

Понятие объема совокупности относится и к выборочной, и к генеральной совокупности.

Пример 2

Пусть из партии 100 пачек масла для исследования выбрано 10 пачек. Тогда объем генеральной совокупности $N=100$, а объем выборки $n=10$.

Примечание 1

Исходя из первых двух определений, очевидно, что всегда выполняется неравенство $N>n$

Помимо этих двух совокупностей выделяют также репрезентативную или представительную выборку.

Определение 4

Репрезентативная (представительная) выборка — выборка, в которой все объекты выбраны случайно и генеральной совокупности, то есть каждый объект генеральной совокупности имеет одинаковую вероятность попасть в выборку.

Выборка также может быть повторной и бесповторной.

Определение 5

Повторная выборка — выборка, при которой выбранный объект возвращается обратно в генеральную совокупность перед выбором следующего объекта для исследования.

Определение 6

Бесповторная выборка — выборка, при которой объект не возвращается обратно в генеральную совокупность перед выбором очередного объекта для исследования.

Определение необходимой численности выборки

Одним из научных принципов в теории выборочного метода является обеспечение достаточного числа отобранных единиц. Теоретически необходимость соблюдения этого принципа представлена в доказательствах предельных теорем теории вероятностей, которые позволяют установить, какой объем единиц следует выбрать из генеральной совокупности, чтобы он был достаточным и обеспечивал репрезентативность выборки.

Уменьшение стандартной ошибки выборки, а следовательно, увеличение точности оценки всегда связано с увеличением объема выборки, поэтому уже на стадии организации выборочного наблюдения приходится решать вопрос о том, каков должен быть объем выборочной совокупности, чтобы была обеспечена требуемая точность результатов наблюдений. Расчет необходимого объема выборки строится с помощью формул, выведенных из формул предельных ошибок выборки (Δ), соответствующих тому или иному виду и способу отбора. Так, для случайного повторного объема выборки (n) имеем:

Суть этой формулы – в том, что при случайном повторном отборе необходимой численности объем выборки прямо пропорционален квадрату коэффициента доверия (t2) и дисперсии вариационного признака (σ2) и обратно пропорционален квадрату предельной ошибки выборки (σ2). В частности, с увеличением предельной ошибки в два раза необходимая численность выборки может быть уменьшена в четыре раза. Из трех параметров два (t и σ) задаются исследователем. При этом исследователь исходя из цели

и задач выборочного обследования должен решить вопрос: в каком количественном сочетании лучше включить эти параметры для обеспечения оптимального варианта? В одном случае его может больше устраивать надежность полученных результатов (t), нежели мера точности (σ), в другом – наоборот. Сложнее решить вопрос в отношении величины предельной ошибки выборки, так как этим показателем исследователь на стадии проектировки выборочного наблюдения не располагает, поэтому в практике принято задавать величину предельной ошибки выборки, как правило, в пределах до 10 % предполагаемого среднего уровня признака. К установлению предполагаемого среднего уровня можно подходить по разному: использовать данные подобных ранее проведенных обследований или же воспользоваться данными основы выборки и произвести небольшую пробную выборку.

Наиболее сложно установить при проектировании выборочного наблюдения третий параметр в формуле (5.2) – дисперсию выборочной совокупности. В этом случае необходимо использовать всю информацию, имеющуюся в распоряжении исследователя, полученную в ранее проведенных подобных и пробных обследованиях.

Вопрос об определении необходимой численности выборки усложняется, если выборочное обследование предполагает изучение нескольких признаков единиц отбора. В этом случае средние уровни каждого из признаков и их вариация, как правило, различны, и поэтому решить вопрос о том, дисперсии какого из признаков отдать предпочтение, возможно лишь с учетом цели и задач обследования.

При проектировании выборочного наблюдения предполагаются заранее заданная величина допустимой ошибки выборки в соответствии с задачами конкретного исследования и вероятность выводов по результатам наблюдения.

В целом формула предельной ошибки выборочной средней величины позволяет определять:

величину возможных отклонений показателей генеральной совокупности от показателей выборочной совокупности;
необходимую численность выборки, обеспечивающую требуемую точность, при которой пределы возможной ошибки не превысят некоторой заданной величины;
вероятность того, что в проведенной выборке ошибка будет иметь заданный предел.

Пример расчета объема выборочной совокупности

Маркетинговая компания получила заказ на проведение социологического исследования с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».

Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95% (одно из стандартных значений для маркетинговых исследований), тогда нормированное отклонение z = 1,96. Проведя предварительный анализ населения города, вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они — «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. исходя из требуемой заказчиком точности, допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.

Подставляем эти данные в формулу и считаем:

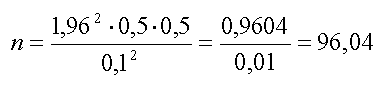
Округлив расчетное значение, получаем объем выборки n = 96 человек.

Следовательно, для проведения исследования с заданными параметрами (уровень доверительности, допустимая ошибка) компании необходимо опросить 96 человек.

Особенности формулы расчета размера выборки

Для рассмотренной нами простой формулы определения объема выборки можно выделить несколько характерных особенностей:

перед тем, как рассчитывать объем выборки в данном случае желательно предварительно провести качественный анализ изучаемой генеральной совокупности. В частности установить степень схожести, близости изучаемых единиц совокупности в части их социальных, демографических, географических, иных характеристик. Также полезно провести пилотное (разведочное) исследование, чтобы установить приблизительную величину p;
нужно иметь в виду, что максимальная изменчивость (вариация ответов) соответствует значению p = 50%, так как тогда q = 50% и p × q = 0,5 × 0,5 = 0,25. Это наихудший случай, все другие значения p дадут изменчивость меньшего размера (например, при p = 80%, p × q = 0,8 × 0,2 = 0,16; а при p = 10%, p × q = 0,1 × 0,9 = 0,09). Впрочем, данный показатель влияет на объем выборки не очень сильно.

Также стоит отметить, что существует ряд иных формул для определения объема выборки в случаях с дихотомической шкалой ответов на единственный вопрос. Для более сложных маркетинговых исследований применяются другие формулы.