Геометрия 8 погорелов: все теоремы и определения

Взаимное отношение хорд и их расстояний от центров

Изобразим окружность и ее элементы, согласно теореме:

Заметим, что радиус, обозначенный, как OC, расположен перпендикулярно к хорде AB, как показано на рисунке:

.

Попробуем доказать следующее:

.

Проведем прямую через точки А и В, которая соединит их с центральной точкой О. Заметим, что наклонные OA и OB равны и удалены от перпендикулярной прямой ОС. В результате:

AD = DB.

Предположим, что перпендикулярная прямая CD выходит из середины AB. В таком случае, точка C равноудалена относительно концов перпендикуляра. Из этого следует равенство хорд AC и CB. Таким образом:

.

Получаем, что перпендикуляр OC делит на две равные части дугу AB, что и требовалось доказать.

Начнем доказательство данного утверждения с того, что центральная точка равноудалена от концов хорды. В таком случае, она будет расположена на перпендикуляре, который восстановлен из середины хорды, что и требовалось доказать.

Перенесем данные на рисунок:

Запишем равенство двух хорд AB и CD:

AB = CD

Представим доказательство того, что данные хорды расположены на одинаковом расстоянии от центральной точки:

OE = OF

Если соединить между собой точки A и C, а также центральную точку O, получим пару треугольников AEO и COF, которые равны и являются прямоугольными. Объясним это равенством радиусов:

OA = OC.

Заметим также, что половины одинаковых хорд будут равны друг другу:

AE = CF.

В результате получим доказательство теоремы:

OE = = OF.

Воспользуемся предыдущим рисунком. Запишем, что хорды AB и CDравноудалены от центра:

OE = OF.

Попробуем подтвердить справедливость следующего равенства:

AB = CD.

Рассмотрим пару прямоугольных треугольников AEO и COF. Данные треугольники равны, исходя из равенства гипотенуз и катетов. Согласно условию:

OE = OF

Равенство радиусов:

OA = OC.

В результате получим, что:

AE = CF

Таким образом, теорема доказана:

AB = CD

Заметим, что хорда AB больше по сравнению с хордой AC:

AB > AC

Требуется доказать следующее:

OD < OE

Заметим, что OD расположен перпендикулярно относительно AB. Линия OF является наклонной. В таком случае:

OD < OF

Запишем, что:

OF < OE

В результате теорема доказана:

OD < OE

«Краткий курс геометрии 8 класс»

«Краткий курс геометрии 8 класс» — это краткие теоретические сведения по курсу геометрии за 8 класс (определения, теоремы, основные свойства). Цитаты взяты в учебных целях из пособия «Геометрия: задачи на готовых чертежах для подготовки к ОГЭ и ЕГЭ (базовый уровень): 8 класс / Э.Н.Бабаян. — Ростов н/Д: Феникс.

Содержание (быстрый переход):

  1. Многоугольник

ABCDE — пятиугольник (рис. 11). Точки А, В, С, D, Е — вершины многоугольника; ∠A, ∠B, ∠C, ∠D, ∠E — углы; АВ, ВС, CD и т. д. — стороны; отрезки АС, AD, BE, BD, СЕ — диагонали; Р = АВ + ВС + … + ЕА — периметр многоугольника.
Многоугольник называется выпуклым (см. рис. 11), если он целиком расположен по одну сторону от каждой прямой, проходящей через две его соседние вершины. В противном случае многоугольник называется невыпуклым (рис. 12).Свойства
1. Сумма внутренних углов произвольного n-угольника равна 180° • (n — 2).
2. Сумма внешних углов выпуклого n-угольника, взятых по одному при каждой вершине, равна 360°.
3. В выпуклом n-угольнике из каждой вершины можно провести (n — 3) диагоналей, которые разбивают n-угольник на (n — 2) треугольников.
4. В выпуклом n-угольнике число диагоналей равно n(n — 3)/2.

  2. Правильные многоугольники

Выпуклый многоугольник, у которого равны все углы и стороны, называется правильным.Свойства
1. Каждый угол правильного n-угольника равен а_n = 180°(n — 2)/n
2. Около правильного n-угольника можно описать окружность, и притом только одну.
3. В правильный n-угольник можно вписать окружность, и притом только одну.
4. Окружность, вписанная в правильный n-угольник, касается всех сторон n-угольника в их серединах.
5. Центр окружности, описанной около правильного n-угольника, совпадает с центром окружности, вписанной в тот же n-угольник.
6. Длина стороны правильного n-угольника, вписанного в окружность радиуса R, равна а = 2R sin(180°/n).
7. Длина стороны правильного n-угольника, описанного около окружности радиуса r, равна а = 2r tg(180°/n).

 4. Параллелограмм

Признаки параллелограмма (рис. 48)

1. Если в четырехугольнике две стороны равны и параллельны (АВ = DC, АВ || CD), то такой четырехугольник — параллелограмм.
2. Если в четырехугольнике противоположные стороны попарно равны (АВ = DC, AD = DC), то такой четырехугольник — параллелограмм.
3. Если в четырехугольнике противоположные углы попарно равны (∠A = ∠C; ∠B = ∠D), то такой четырехугольник — параллелограмм.
4. Если в четырехугольнике диагонали пересекаются и в точке пересечения делятся пополам, то такой четырехугольник — параллелограмм.

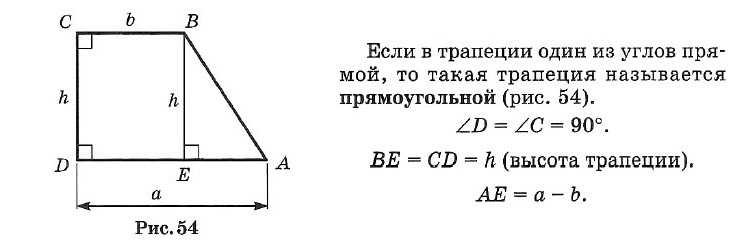
Равнобедренная трапеция

Прямоугольная трапеция

 18. Окружность

Окружностью называется геометрическое место точек плоскости, равноудаленных от одной ее точки (центра) (рис. 37).
Отрезок, соединяющий центр окружности с точкой на окружности, называется радиусом. Обозначение: г или R.
На рисунке ОС = ОЕ = OD = R.
Часть окружности (например, CmD) называется дугой.
Отрезок, соединяющий две точки окружности, называется хордой, а хорда, проходящая через центр, — диаметром.
АВ, ВС, CD и СЕ — хорды окружности. СЕ — наибольшая из хорд — диаметр.
Обозначение: d или D. D = 2R.
Часть плоскости, ограниченная окружностью, называется кругом.
Часть круга, ограниченная дугой (CmD) и стягивающей ее хордой (CD), называется сегментом.
Часть круга, ограниченная двумя радиусами и дугой, называется сектором.
Угол, образованный двумя радиусами, называется центральным (∠COD на рис. 37).
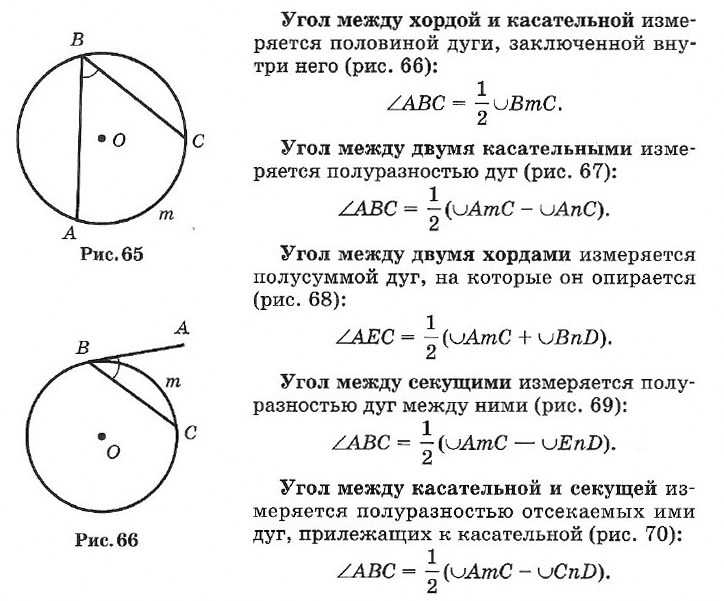
Угол, у которого вершина лежит на окружности, а стороны являются хордами, называется вписанным (например, ∠ABC).

  19. Свойства касательных к окружности

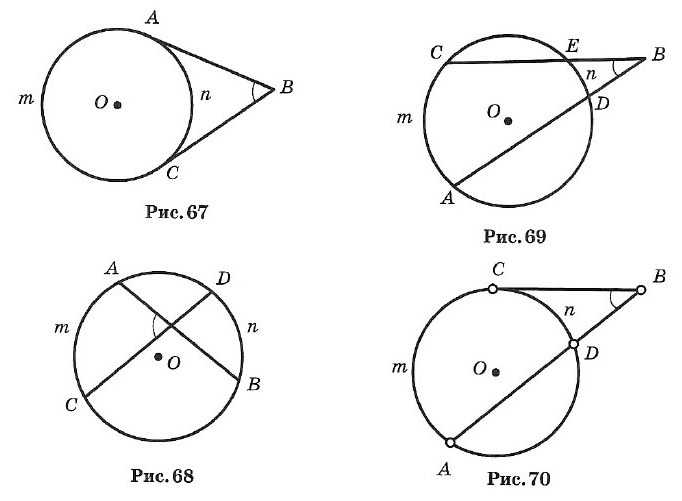
Угол, образованный двумя касательными (СА и СВ), исходящими из одной точки, называется описанным (∠ACB на рис. 38).
1. Радиус, проведенный в точку касания, перпендикулярен касательной.
2. Две касательные, проведенные к окружности из одной точки, равны, и центр окружности лежит на биссектрисе угла между ними.

  20. Окружность и треугольник

1. Около всякого треугольника можно описать окружность; центром окружности является точка пересечения перпендикуляров, проведенных к сторонам через их середины (рис. 39).
2. Во всякий треугольник можно вписать окружность; центром окружности является точка пересечения биссектрис (рис. 40).

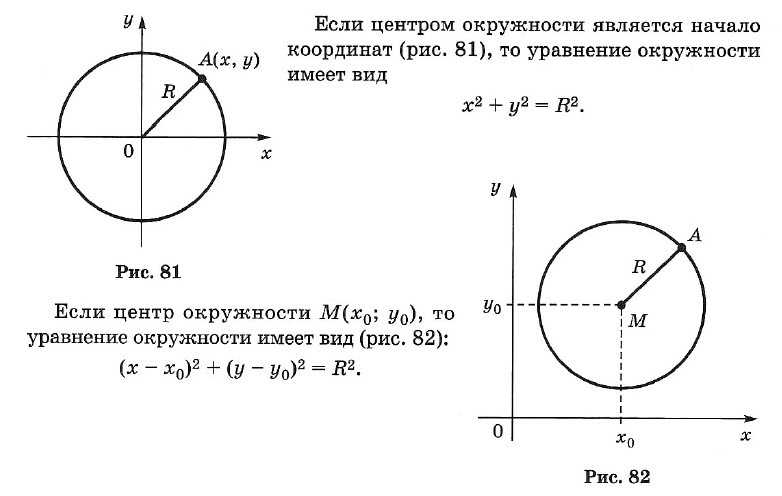
 25. Уравнение окружности

Вы смотрели «Краткий курс геометрии 8 класс» — все определения, теоремы и основные свойства из Геометрии за 8 класс. Выберите дальнейшие действия:

• Посмотреть Краткий курс геометрии за 7 класс 
• Вернуться к Списку конспектов по геометрии

Все правила и теоремы по геометрии за 8 класс

Успейте воспользоваться скидками до 50% на курсы «Инфоурок» Геометрия,7-9 Основные определения, теоремы, формулы 7 класс Глава I Начальные геометрические сведения Первичные понятия: точка, прямая, плоскость, пространство, отрезок, луч, угол, равные фигуры, середина отрезка, биссектриса угла, измерение отрезков, измерение углов Отрезок-часть прямой, ограниченная двумя точками.

Луч-часть прямой,ограниченная точкой с одной стороны и неограниченная с другой стороны. Угол-часть плоскости, ограниченная двумя лучами, выходящими из одной точки. Равные фигуры-фигуры, которые совпадают при наложении друг на друга.

Середина отрезка-точка на отрезке, делящая его пополам. Биссектриса угла-луч, выходящий из вершины угла и делящий его пополам. Единицы измерения длины отрезка: миллиметры, сантиметры, дециметры, метры, километры.

Единицы измерения углов: градус, минуты, секунды. Длина отрезка-количество единиц измерения длины, вмещающихся между двумя концами отрезка. Градусная мера угла-количество единиц измерения углов, вмещающихся между сторонами угла. Прямой угол-угол,градусная мера которого равна 90 0 . Острый угол-угол,градусная мера которого меньше 90 0 .

Развёрнутый угол-угол,градусная мера которого равна 180 0 . Смежные углы – это два угла, у которых одна сторона общая,а две других образуют прямую линию. Свойство: сумма смежных углов равна 180 0 .

Вертикальные углы-два угла, у которых стороны одного угла являются продолжением сторон другого.

Свойство: вертикальные углы равны. Перпендикулярные прямые-прямые, которые при пересечении образуют прямой угол.

Параллельные прямые-прямые, лежащие в одной плоскости и не имеющие общих точек.

Глава II Треугольники Треугольник-фигура, состоящая из трёх точек, соединённых между собой отрезками.Точки-вершины треугольника, отрезки-стороны треугольника. Периметр – сумма длин всех сторон. Теорема(первый признак равенства треугольников): если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Теорема: из точки,не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один. Медиана треугольника— это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектриса треугольника— отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. Высота треугольника— перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

Равнобедренный треугольник-треугольник, у которого две стороны равные. Равные стороны – боковые, третья сторона – основание.

Равносторонний треугольник— треугольник, у которого все стороны равны. Свойство:в равнобедренном треугольнике углы при основании равны.

Свойство:в равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой. Теорема(второй признак равенства треугольников): если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Раздел 1. Четырёхугольники

Определение четырёхугольника

Четырёхугольником называется фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Данные точки называются вершинами четырёхугольника, а соединяющие их отрезки — сторонами четырёхугольника.

Четырёхугольник называется вписанным, если все его вершины лежат на некоторой окружности, и описанным, если все его стороны касаются некоторой окружности.

Вершины четырёхугольника называются соседними, если они являются концами одной из его сторон. Вершины, не являющиеся соседними, называются противолежащими. Отрезки, соединяющие противолежащие вершины четырёхугольника, называются диагоналями.

Стороны четырёхугольника, исходящие из одной вершины, называются соседними сторонами. Стороны, не имеющие общего конца, называются противолежащими сторонами.

Четырёхугольник обозначается указанием его вершин. Например, ABCD. В обозначении четырёхугольника рядом стоящие вершины должны быть соседними. Четырёхугольник ABCD можно также обозначить BCDA или DCBA. Но нельзя обозначить ABDC (В и D — не соседние вершины).

Сумма длин всех сторон четырёхугольника называется периметром.

Параллелограмм

Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны, т. е. лежат на параллельных прямых.

Теорема 6.1. Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм.

Свойство диагоналей параллелограмма

Теорема 6.2. (обратная теореме 6.1) Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Прямоугольник — это параллелограмм, у которого все углы прямые.

Теорема 6.4. Диагонали прямоугольника равны.

Ромб

Ромб — это параллелограмм, у которого все стороны равны.

Теорема 6.5. Диагонали ромба пересекаются под прямым углом. Диагонали ромба являются биссектрисами его углов.

Квадрат

Квадрат — это прямоугольник, у которого все стороны равны. Так как стороны квадрата равны, то он является также ромбом. Поэтому квадрат обладает свойствами прямоугольника и ромба.

1. У квадрата все углы прямые.
2. Диагонали квадрата равны.
3. Диагонали квадрата пересекаются под прямым углом и являются биссектрисами его углов.

Теорема Фалеса

Теорема 6.6. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Замечание. В условии теоремы Фалеса вместо сторон угла можно взять любые две прямые, при этом заключение теоремы будет то же: параллельные прямые, пересекающие две данные прямые и отсекающие на одной прямой равные отрезки, отсекают равные отрезки и на другой прямой.

Средняя линия треугольника

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Теорема 6.7. Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна её половине.

Трапеция

Трапецией называется четырёхугольник, у которого только две противолежащие стороны параллельны. Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами.

Теорема 6.8. Средняя линия трапеции параллельна основаниям и равна их полусумме.

Замечательные точки в треугольнике

Все три биссектрисы треугольника пересекаются в одной точке. Все три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке. Все три прямые, содержащие высоты к сторонам треугольника, тоже пересекаются в одной точке (ортоцентр треугольника). Все три медианы треугольника пересекаются в одной точке.

Окружность, описанную около треугольника, вершинами которого являются середины сторон данного треугольника, называют окружностью Эйлера (окружность девяти точек). Середины сторон треугольника и середины отрезков, соединяющих его ортоцентр с вершинами, лежат на одной окружности с центром О, являющейся по определению окружностью Эйлера.

Виды окружностей — вписанные и описанные окружности

Какой-либо без ограничений многоугольник, являющийся правильным, допустимо вписать в окружность. На рисунке изображена описанная около шестиугольника окружность, которая проходит через все его вершины:

Запишем свойства, которые характерны для описанной около треугольника окружности:

1. Около какого-либо треугольника допустимо описать единственную окружность.
2. Если окружность описана около прямоугольного треугольника, то ее центральная точка располагается на середине гипотенузы.
3. Окружность, описанная около треугольника, имеет радиус, который определяют, как отношение произведения сторон a, b, c треугольника к его учетверенной площади: .
4. Окружность, описанная около треугольника, имеет радиус, который определяют, как отношение стороны треугольника к удвоенному синусу противолежащего угла: .

В том случае, когда окружность описана около четырехугольника, она обладает следующими свойствами:

1. Около какого-либо четырехугольника допустимо описать окружность при условии, что его противоположные углы в сумме дают .
2. Вписанный в окружность четырехугольник имеет диагонали, произведение которых соответствует сумме произведений противоположных сторон.
3. Если четырехугольник вписан в окружность, то его площадь определяют с помощью формулы Брахмагупты: 

Заметим, что в какой-либо многоугольник, который является правильным, допустимо вписать окружность. Продемонстрируем это с помощью рисунка, на котором изображена окружность, вписанная в правильный многоугольник с шестью углами и касающаяся каждой его стороны:

Вписанная окружность обладает следующими свойствами:

1. Центральная точка окружности, вписанной в многоугольник, совпадает с точкой пересечения биссектрис внутренних углов данного многоугольника.
2. В какой-либо треугольник допустимо вписать единственную окружность.
3. Вписанная окружность имеет радиус, равный отношению площади треугольника к половине его периметра: .
4. Вписать окружность в четырехугольник допустимо при условии, что данный четырехугольник является выпуклым.
5. Окружность допустимо вписать в выпуклый четырехугольник в том случае, когда соблюдается равенство сумм его противолежащих сторон.

Определения и свойства окружности

Введем несколько определений, связанных с темой окружности. Данные термины можно встретить на уроках в седьмом классе и других курсах по алгебре и геометрии.

1 Примечание 1

В распространенных случаях возникает путаница в понятиях окружности и круга. Заметим, что кругом может называться множество точек на плоскости, которые при построении ограничены окружностью, то есть данные точки расположены во внутренней области окружности.

Окружность обладает рядом свойств:

1. Если три точки на плоскости не принадлежат общей прямой, то через них допустимо построить единственную окружность.
2. Точка (С), в которой касаются две окружности, расположена на общей с центрами этих окружностей прямой (АВ).
3. Изопериметрическое неравенство: из всех замкнутых кривых на графике, имеющих одинаковую длину, окружность ограничивает область с максимальной площадью.

При решении самостоятельных работ и задач на некоторые окружности пригодятся следующие формулы, чтобы находить ключевые параметры:

Диаметр окружности можно высчитать таким образом:

Длина окружности в теории:

Радиус окружности можно узнать с помощью формулы:

Раздел 2. Теорема Пифагора

Косинус угла

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Косинус угла а обозначается так: cos а и равен отношению катета АС, прилежащего к этому углу, к гипотенузе АВ, т. е. cos a = АС/АВ.

Теорема 7.1. Косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника.

Это означает, что у двух прямоугольных треугольников с одним и тем же острым углом косинусы этого угла равны.

Теорема Пифагора

Теорема 7.2. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Из теоремы Пифагора следует, что в прямоугольном треугольнике любой из катетов меньше гипотенузы. Отсюда, в свою очередь, следует, что cos а < 1 для любого острого угла а.

Египетский треугольник

Землемеры Древнего Египта для построения прямого угла пользовались следующим приёмом. Бечёвку узлами делили на 12 равных частей и концы связывали. Затем бечёвку растягивали на земле так, что получался треугольник со сторонами 3, 4 и 5 делений. Угол треугольника, противолежащий стороне с 5 делениями, был прямой (32 + 42= 52).

В связи с указанным способом построения прямого угла треугольник со сторонами 3, 4 и 5 единиц иногда называют египетским.

Перпендикуляр и наклонная

Пусть ВА — перпендикуляр, опущенный из точки В на прямую а, и С — любая точка прямой а, отличная от А. Отрезок ВС называется наклонной, проведённой из точки В к прямой а (рис. 153). Точка С называется основанием наклонной. Отрезок АС называется проекцией наклонной.

Из теоремы Пифагора следует, что если к прямой из одной точки проведены перпендикуляр и наклонные, то любая наклонная больше перпендикуляра, равные наклонные имеют равные проекции, из двух наклонных больше та, у которой проекция больше.

Неравенство треугольника

Если точки А и В различны, то расстоянием между ними называется длина отрезка АВ. Если точки А и В совпадают, то расстояние между ними принимается равным нулю.

Теорема 7.3. Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки.

Это значит, что каждое из этих расстояний меньше суммы или равно сумме двух других. Заметим, что в случае, когда точки не лежат на одной прямой, в неравенстве треугольника строгое неравенство. Отсюда следует, что в любом треугольнике каждая сторона меньше суммы двух других сторон.

Соотношения между сторонами и углами в прямоугольном треугольнике

Пусть АВС — прямоугольный треугольник с прямым углом С и острым углом при вершине А, равным а.

• Согласно определению cos а равен отношению катета, прилежащего к углу а, к гипотенузе.
• Синусом угла а (обозначается sin а) называется отношение противолежащего катета ВС к гипотенузе АВ: sin а = ВС/АВ.
• Тангенсом угла а (обозначается tg a) называется отношение противолежащего катета ВС к прилежащему катету АС: tg a = ВС/АС.
• Котангенсом угла а (обозначается ctg a) называется отношение прилежащего катета АС к противолежащему катету ВС: ctga = АС/ВС.

Синус, тангенс и котангенс утла, так же как и косинус, зависят только от величины угла. Из определения sin a, cos a, tg a и ctg a получаем следующие правила:

1. Катет, противолежащий углу а, равен произведению гипотенузы на sin a.
2. Катет, прилежащий к углу а, равен произведению гипотенузы на cos a.
3. Катет, противолежащий углу а, равен произведению второго катета на tg a.
4. Катет, прилежащий к углу а, равен произведению второго катета на ctg a.

Эти правила позволяют, зная одну из сторон прямоугольного треугольника и острый угол, находить две другие стороны; зная две стороны, находить острые углы.

Для sin a, cos a, tg a и ctg a составлены специальные таблицы. Эти таблицы позволяют по данному углу а найти sin a, cos a, tg a и ctg a или по значениям sin a, cos a, tg a и ctg a найти соответствующий угол. В настоящее время для этой цели обычно применяют микрокалькуляторы.

Основные тригонометрические тождества

Эти тождества позволяют, зная одну из величин sin a, cos a, tg a или ctg a, найти три другие.

1. tg a = sin a / cos a.
2. сtg a = cos a / sin a.
3. sin2a + cos2a = 1.
4. 1 + tg2a = 1 / cos2a
5. 1 + ctg2a = 1 / sin2a

advocate-general.com

20.

Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.

30. Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции.

40. Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию. 6.11. Свойство второй средней линии трапеции: Пусть средняя КN-вторая средняя линия трапеции с основаниями ВС и АD, проходящая через точку пересечения диагоналей трапеции М.

Следовало объяснить: «Что означает треугольник, вписанный в круг?» Человек проводил 12 часов наедине с этой задачей, имея кружку воды и кусок хлеба; затем его вводили в залу собраний, где были в сборе все ученики, которые должны были провоцировать его па негодование — смеяться и т. п.— а он — показать свой разум и воздержанность; многие плакали, грубили, бросали доску, бранили школу и т. п.; тогда выходил Пифагор и объявлял, выдержал ли испытуемый экзамен и принят ли в школу).

Как попасть в Пифагорейскую школу ?

? Пифагорейцы занимались математикой, философией, естественными науками. Ими было сделано много важных открытий в арифметике и геометрии. В школ существовал декрет, по которому авторство всех математических работ приписывалось Пифагору.

7.7. Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы, косинусы и тангенсы этих углов равны.

8.1. Если расстояние от центра окружности до прямой меньше радиуса окружности (d),> 8.2. Если расстояние от центра окружности до прямой равно радиусу окружности (d=r), то прямая и окружность имеют только одну общую точку.

8.3. Если расстояние от центра окружности до прямой больше радиуса окружности (dr), то прямая и окружность не имеют общих точек.

8.4. Теорема (о касательной и радиусе). Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. 8.5. Отрезки касательных к окружности, проведенные из одной точки.

Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому,как вычисляется гипотенуза прямоугольного треугольника с катетами a и b Мы имеем d?=a?+b?

СТРОИТЕЛЬСТВО ОКНА КРЫШИ МОЛНИЕОТВОДЫ ОКНО В зданиях готического и ромaнского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон.

На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны ширине окна для наружных дуг и половине ширины для внутренних дуг. Остается еще полная окружность, касающаяся четырех дуг.

«Краткий курс геометрии 8 класс»

«Краткий курс геометрии 8 класс» — это краткие теоретические сведения по курсу геометрии за 8 класс (определения, теоремы, основные свойства). Цитаты взяты в учебных целях из пособия «Геометрия: задачи на готовых чертежах для подготовки к ОГЭ и ЕГЭ (базовый уровень): 8 класс / Э.Н.Бабаян. — Ростов н/Д: Феникс.

ABCDE — пятиугольник (рис. 11). Точки А, В, С, D, Е — вершины многоугольника; ∠A, ∠B, ∠C, ∠D, ∠E — углы; АВ, ВС, CD и т. д. — стороны; отрезки АС, AD, BE, BD, СЕ — диагонали; Р = АВ + ВС + … + ЕА — периметр многоугольника.
Многоугольник называется выпуклым (см. рис. 11), если он целиком расположен по одну сторону от каждой прямой, проходящей через две его соседние вершины. В противном случае многоугольник называется невыпуклым (рис. 12).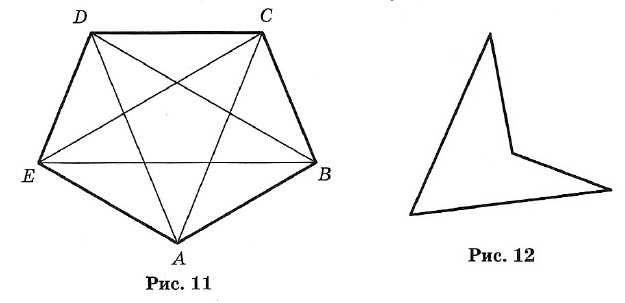Свойства
1. Сумма внутренних углов произвольного n-угольника равна 180° • (n — 2).
2. Сумма внешних углов выпуклого n-угольника, взятых по одному при каждой вершине, равна 360°.
3. В выпуклом n-угольнике из каждой вершины можно провести (n — 3) диагоналей, которые разбивают n-угольник на (n — 2) треугольников.
4. В выпуклом n-угольнике число диагоналей равно n(n — 3)/2.

Выпуклый многоугольник, у которого равны все углы и стороны, называется правильным.Свойства
1. Каждый угол правильного n-угольника равен а_n = 180°(n — 2)/n
2. Около правильного n-угольника можно описать окружность, и притом только одну.
3. В правильный n-угольник можно вписать окружность, и притом только одну.
4. Окружность, вписанная в правильный n-угольник, касается всех сторон n-угольника в их серединах.
5. Центр окружности, описанной около правильного n-угольника, совпадает с центром окружности, вписанной в тот же n-угольник.
6. Длина стороны правильного n-угольника, вписанного в окружность радиуса R, равна а = 2R sin(180°/n).
7. Длина стороны правильного n-угольника, описанного около окружности радиуса r, равна а = 2r tg(180°/n).

Признаки параллелограмма (рис. 48)

1. Если в четырехугольнике две стороны равны и параллельны (АВ = DC, АВ || CD), то такой четырехугольник — параллелограмм.
2. Если в четырехугольнике противоположные стороны попарно равны (АВ = DC, AD = DC), то такой четырехугольник — параллелограмм.
3. Если в четырехугольнике противоположные углы попарно равны (∠A = ∠C; ∠B = ∠D), то такой четырехугольник — параллелограмм.
4. Если в четырехугольнике диагонали пересекаются и в точке пересечения делятся пополам, то такой четырехугольник — параллелограмм.

Равнобедренная трапеция

Прямоугольная трапеция

Окружностью называется геометрическое место точек плоскости, равноудаленных от одной ее точки (центра) (рис. 37).
Отрезок, соединяющий центр окружности с точкой на окружности, называется радиусом. Обозначение: г или R.
На рисунке ОС = ОЕ = OD = R.
Часть окружности (например, CmD) называется дугой.
Отрезок, соединяющий две точки окружности, называется хордой, а хорда, проходящая через центр, — диаметром.
АВ, ВС, CD и СЕ — хорды окружности. СЕ — наибольшая из хорд — диаметр.
Обозначение: d или D. D = 2R.
Часть плоскости, ограниченная окружностью, называется кругом.
Часть круга, ограниченная дугой (CmD) и стягивающей ее хордой (CD), называется сегментом.
Часть круга, ограниченная двумя радиусами и дугой, называется сектором.
Угол, образованный двумя радиусами, называется центральным (∠COD на рис. 37).
Угол, у которого вершина лежит на окружности, а стороны являются хордами, называется вписанным (например, ∠ABC).

Угол, образованный двумя касательными (СА и СВ), исходящими из одной точки, называется описанным (∠ACB на рис. 38).
1. Радиус, проведенный в точку касания, перпендикулярен касательной.
2. Две касательные, проведенные к окружности из одной точки, равны, и центр окружности лежит на биссектрисе угла между ними.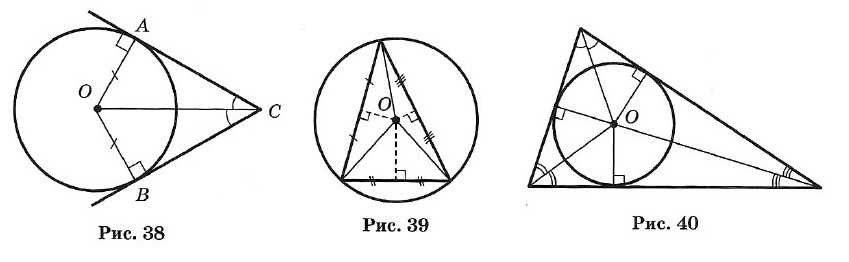

1. Около всякого треугольника можно описать окружность; центром окружности является точка пересечения перпендикуляров, проведенных к сторонам через их середины (рис. 39).
2. Во всякий треугольник можно вписать окружность; центром окружности является точка пересечения биссектрис (рис. 40).

Вы смотрели «Краткий курс геометрии 8 класс» — все определения, теоремы и основные свойства из Геометрии за 8 класс. Выберите дальнейшие действия:

• Посмотреть Краткий курс геометрии за 7 класс 
• Вернуться к Списку конспектов по геометрии

Раздел 5. Векторы

Абсолютная величина и направление вектора

Вектор — это направленный отрезок. Направление вектора определяется указанием его начала и конца. На чертеже направление вектора отмечается стрелкой. Для обозначения векторов будем пользоваться строчными латинскими буквами а, b, с, … . Можно также обозначать вектор указанием его начала и конца. При этом начало вектора ставится на первом месте. Вместо слова «вектор» над буквенным обозначением вектора иногда ставится стрелка или черта.

Векторы АВ и CD называются одинаково направленными, если полупрямые АВ и CD одинаково направлены. Векторы АВ и CD называются противоположно направленными, если полупрямые АВ и CD противоположно направлены.

Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор.

Начало вектора может совпадать с его концом. Такой вектор будем называть нулевым вектором. Нулевой вектор обозначается нулём с чёрточкой (0). О направлении нулевого вектора не говорят. Абсолютная величина нулевого вектора считается равной нулю.

Равенство векторов

Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора. Из данного определения равенства векторов следует, что

равные векторы одинаково направлены и равны по абсолютной величине. Обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны.

Координаты вектора

Пусть вектор а имеет началом точку А1 (х1; у1), а концом точку А2 (х2; у2). Координатами вектора а будем называть числа а1 = х2 – х1, а2 = у2 – у1. Координаты нулевого вектора равны нулю.

Равные векторы имеют равные соответствующие координаты. И обратно: если у векторов соответствующие координаты равны, то векторы равны.

Сложение векторов

Суммой векторов а и b с координатами а1, а2 и b1, b2 называется вектор с с координатами a1 +b1, a2 + b2.

Теорема 10.1. Каковы бы ни были точки А, В, С, имеет место векторное равенство АВ + ВС = АС.

Сложение сил

Силу, приложенную к телу, удобно изображать вектором, направление которого совпадает с направлением действия силы, а абсолютная величина пропорциональна величине силы. Как показывает опыт, при таком способе изображения сил равнодействующая двух или нескольких сил, приложенных к телу в одной точке, изображается суммой соответствующих им векторов.

Представление силы в виде суммы сил, действующих в двух заданных направлениях, называется разложением силы по этим направлениям. Удобно производить разложение вектора по двум перпендикулярным осям. В этом случае составляющие вектора называются проекциями вектора на оси.

Умножение вектора на число

Произведением вектора (а1; а2) на число λ называется вектор (λа1; λа2).

Теорема 10.2. Абсолютная величина вектора λа равна |λ| |a|. Направление вектора λа при а ≠ 0 совпадает с направлением вектора а, если λ > 0, и противоположно направлению вектора а, если λ < 0.

Разложение вектора по двум неколлинеарным векторам

Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные векторы направлены либо одинаково, либо противоположно.

Пусть а и b — отличные от нулевого неколлинеарные векторы, тогда любой вектор с можно представить в виде с = λа + ɳb.

Скалярное произведение векторов

Скалярным произведением векторов a(a1; a2) и b(b1; b2) называется число а1b1 + а2b2. Скалярное произведение а • а обозначается а2 и называется скалярным квадратом.

Для любых векторов а(а1; а2), b(b1; b2), с(с1; с2)(а + b) • с = ас + bс.

Теорема 10.3. Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.

Из теоремы 10.3 следует, что если векторы перпендикулярны, то их скалярное произведение равно нулю. И обратно: если скалярное произведение отличных от нулевого векторов равно нулю, то векторы перпендикулярны.

Разложение вектора по координатным осям

Вектор называется единичным, если его абсолютная величина равна единице. Единичные векторы, имеющие направления положительных координатных полуосей, называются координатными векторами или ортами.

Для любого вектора a (a1; а2) получается разложение а = а1е1 + а2е2.

Вы смотрели «Геометрия 8 Погорелов: все теоремы и определения» — краткое повторение геометрии за 8 класс (основные понятия, определения и теоремы без доказательств).