Ряды динамики

Приведение рядов динамики к одинаковому основанию

Во время работы с несколькими явлениями, описывающими один процесс, может вызывать интерес сопоставление рядов динамики. С целью корректного сопоставления потребуется приведение к одному основанию. Сопутствующей операцией является вычисление коэффициента опережения или отставания.

К каждому ряду находится базисный уровень и вычисляются темпы роста и прироста рядов. Для каждого ряда должен быть выбран аналогичный временной интервал.

Сравнение проводится на основании отношения базисного темпа роста (опционально – прироста) в аналогичном временной интервале. Выражения для расчета достаточно просты:

Пример ряда динамики и его характеристика

В качестве примера, рассмотрим следующий ряд.

Таблицу можно озаглавить так: «Годовой выпуск препарата «Ибупрофен» в 2013-2018гг. в млн. уп.»

Год	2013	2014	2015	2016	2017	2018
Годовой объем выпуска, млн. уп.	88,1	91,3	96,5	99,3	101,8	100,7

В данном ряду можно обнаружить присутствие следующих показателей:

• имеется показатель t, которому соответствует строка «Год», содержащая информацию о периоде, за который выпускался препарат «Ибупрофен»,
• имеется показатель у, который показывает годовой объем производства препарата «Ибупрофен»,
• показатели t и у соотнесены.

На основании изложенного, можно сделать вывод, что перед нами находится временной ряд.

Средние показатели ряда динамики

Каждый ряд динамики можно рассматривать как некую совокупность n меняющихся во времени показателей, которые можно обобщать в виде средних величин. Такие обобщенные (средние) показатели особенно необходимы при сравнении изменений того или иного показателя в разные периоды, в разных странах и т.д.

Обобщенной характеристикой ряда динамики может служить прежде всего средний уровень ряда. Способ расчета среднего уровня зависит от того, моментный ряд или интервальный (периодный).

В случае интервального ряда его средний уровень определяется по формуле из уровней ряда, т.е.

=
Если имеется моментный ряд, содержащий n уровней (y1, y2, …, yn) с равными промежутками между датами (моментами времени), то такой ряд легко преобразовать в ряд средних величин. При этом показатель (уровень) на начало каждого периода одновременно является показателем на конец предыдущего периода. Тогда средняя величина показателя для каждого периода (промежутка между датами) может быть рассчитана как полусумма значений у на начало и конец периода, т.е. как . Количество таких средних будет . Как указывалось  ранее, для рядов средних величин средний уровень рассчитывается по средней арифметической. Следовательно, можно записать.
После преобразования числителя получаем,

Y1 Yn Yi 

Эта средняя  известна в статистике как средняя хронологическая для моментных рядов. Такое название она получила от слова «cronos» (время, лат.), так как рассчитывается из меняющихся во времени показателей.

В случае неравных промежутков между датами среднюю хронологическую для моментного ряда можно рассчитать как среднюю арифметическую из средних значений уровней на каждую пару моментов, взвешенных по величине расстояний (отрезков времени) между датами, т.е..
В данном случае предполагается, что в промежутках между датами уровни принимали разные значения, и мы из двух известных (yi и yi+1) определяем средние, из которых затем уже рассчитываем общую среднюю для всего анализируемого периода.
Если же предполагается, что каждое значение yi  остается неизменным до следующего (i+1)-го момента, т.е. известна  точная дата изменения уровней, то расчет можно осуществлять по формуле средней арифметической взвешенной:,

Кроме среднего уровня в рядах динамики рассчитываются и другие средние показатели – среднее изменение уровней ряда (базисным и цепным способами), средний темп изменения.

Базисное среднее абсолютное изменение представляет собой частное от деления последнего базисного абсолютного изменения на количество изменений. То есть

Б =

Цепное среднее абсолютное изменение уровней ряда представляет собой частное от деления суммы всех цепных абсолютных изменений на количество изменений, то есть

Ц =

По знаку средних абсолютных изменений также судят о характере изменения явления в среднем: рост, спад или стабильность.

Из следует, что базисное и цепное среднее изменение должны быть равными.

Наряду со средними абсолютным изменением рассчитывается и среднее относительное тоже базисным и цепным способами.

Базисное среднее относительное изменение определяется по формуле

Б==

Цепное среднее относительное изменение определяется по формуле

Ц=

Естественно, базисное и цепное среднее относительное изменения должны быть одинаковыми и сравнением их с критериальным значением 1 делается вывод о характере изменения явления в среднем: рост, спад или стабильность.
Вычитанием 1 из базисного или цепного среднего относительного изменения образуется соответствующий средний темп изменения, по знаку которого также можно судить о характере изменения изучаемого явления, отраженного данным рядом динамики.

Предыдущая лекция…

Понятие рядов динамики (временных рядов)

Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, то есть их динамика. Эта задача решается при помощи анализа рядов динамики (временных рядов).

Ряд динамики (или временной ряд) – это числовые значения определенного статистического показателя в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке).

Числовые значения того или иного статистического показателя, составляющего ряд динамики, называют уровнями ряда и обычно обозначают буквой y. Первый член ряда y₁ называют начальным или базисным уровнем, а последний y_n – конечным. Моменты или периоды времени, к которым относятся уровни, обозначают через t.

Ряды динамики, как правило, представляют в виде или , причем по оси абсцисс строится шкала времени t, а по оси ординат – шкала уровней ряда y.

Пример ряда динамики

Таблица. Число жителей России в 2004-2009 гг. в млн.чел, на 1 января

Год	2004	2005	2006	2007	2008	2009
Число жителей	144,2	143,5	142,8	142,2	142,0	141,9

График ряда динамики числа жителей России в 2004-2009 гг. в млн.чел, на 1 января

Данные и наглядно иллюстрируют ежегодное снижение числа жителей России в 2004-2009 годах.

Методы выравнивания рядов динамики

Выравнивание используется для определения общего направления динамики процессов. Кратковременные случайные всплески роста / падения иногда нарушают целостность восприятия картины. 

Ещё можно заметить, что:

1. Увеличение периодов позволяет построить данные таким образом, чтобы изменения явно демонстрировали основную линию. Выравниваются средние значения.

2. Плавающая средняя означает, что она подсчитывается из определенного числа соседних уровней. По новым правилам построения организуется новый ряд из средних. Метод оптимален, если графическая интерпретация близка к прямой. В противном случае искажение динамики может оказаться чрезмерным.

3. Аналитический метод сводится к аппроксимации параметров математическим уравнением с высокой корреляцией. Дальнейшая работа базируется на нем. Так легче выявить тенденцию, можно позволить какие-то прогнозы. Облегчается использование численных методов.

Средние значения показателей рядов динамики

Средние значения показателей рядов динамики выражают уровни и типичные значения их изменений
в определённый период времени. Прежде чем рассматривать средние значения показателей рядов динамики, разграничим
понятия интервальных и моментных рядов динамики.

Интервальные ряды динамики характеризуют значения изучаемого явления за некоторый
период времени, например, за месяц, за год, за пять лет. Моментные ряды динамики характеризуют значения
изучаемого явления в какой-то определённый момент времени, например, на начало или конец месяца, начало
или конец года и так далее. В предыдущем параграфе мы рассматривали интервальный ряд динамики и его
показатели.

Средний уровень интервального ряда динамики вычисляется путём деления суммы уровней
ряда на число уровней:

.

Пример 5. Вычислить среднегодовой объём экспорта предприятия «Х».

Решение. Вычислим средний уровень по формуле для интервального ряда динамики:

Средний уровень моментного ряда динамики, если между моментами — равные
промежутки времени, вычисляется по формуле средней хронологической:

.

Пример 6. Вычислить среднее число сотрудников предприятия «Х» на
начало года. В таблице ниже даны значения числа сотрудников на начало каждого года с 2013 по 2017 годы.

Момент	Число
1 янв. 2013	1113
1 янв. 2014	1122
1 янв. 2015	1110
1 янв. 2016	1130
1 янв. 2017	1222

Решение. Вычисляем по формуле хронологической средней:

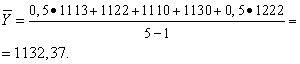
Если между моментами ряда динамики — не равные промежутки времени, средний уровень
моментного ряда вычисляется по формуле средней хронологической взвешенной:

В этой формуле
— — уровни ряда динамики,
— — периоды
времени, например, 1 месяц, 2 месяца, 1 год, 2 года, 3 года… Все периоды времени должны выражаться в одной
и той же единице измерения (днях, месяцах, годах и др.).

Средний абсолютный прирост (снижение) выражает абсолютную величину, на которую в
среднем в каждую единицу времени в соответствующий период выросли или снизились показатели исследуемого
явления. Его вычисляют путём деления суммы цепных абсолютных приростов на число абсолютных приростов:

,

где —
число абсолютных приростов.

Если нет данных о цепных абсолютных приростах, но известны начальный и конечный уровни
ряда динамики, то средний абсолютный прирост можно вычислить через базовый абсолютный прирост по формуле

.

Пример 7. Используя данные об экспорте предприятия «Х», вычислить
среднегодовой прирост экспорта.

Решение. Вычислим интересующий нас показатель через сумму цепных абсолютных приростов:

.

Вычислим его же через базовый абсолютный прирост:

.

Как видим, получили один и тот же результат.

Средний темп роста является показателем изменения интенсивности изменения уровней ряда
динамики. Он характеризует среднюю интенсивность развития исследуемого явления, показывая, во сколько раз
в среднем в единицу времени изменились уровни ряда динамики. Средний темп роста можно выразить в
коэффициентах или процентах.

Цепной средний темп роста вычисляется по формуле среднего геометрического:

,

где n — число цепных темпов роста,

T — индивидуальные цепные темпы роста, выраженные в коэффициентах.

Если нет информации о каждом цепном темпе роста, средний темп роста можно вычислить
по формуле с использованием последнего и первого уровней ряда динамики

.

Пример 8. Вычислить средний темп роста экспорта предприятия «Х».

Решение. Вычисляем по формуле среднего геометрического:

Вычисляем по формуле с использованием последнего и первого уровней ряда динамики:

.

Получили один и тот же результат.

Средний темп прироста показывает, на сколько процентов в среднем увеличился (если
он со знаком «плюс») или уменьшился (если со знаком «минус») уровень исследуемого явления в течение
всего рассматриваемого периода. Средний темп прироста вычисляется путём вычитания из среднего темпа
роста 100% (если он выражен в процентах) или единицы (если он выражен в виде коэффициента).

В нашем примере:

Виды рядов динамики

В зависимости от характеризующего критерия, существует несколько разновидностей динамических рядов.

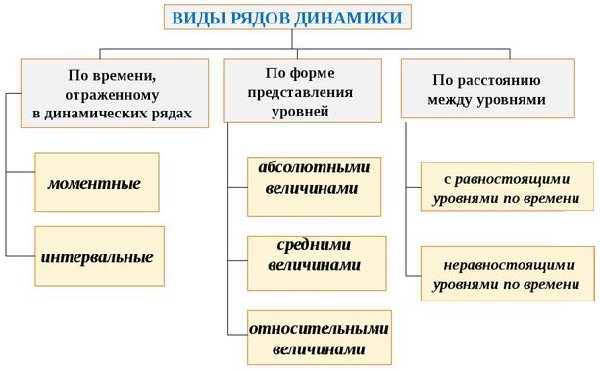
По временной характеристике различают моментальные и интервальные:

1. Для интервальных рядов характерна результативность. Иными словами такой ряд может состоять из суммарной характеристики, которая произошла на данный момент времени t (например, сколько продукции произведено на момент времени, сколько человеко-дней зарегистрировано за определенный период).
2. Для моментальных рядов характерно мгновенное значение изучаемой характеристики. К таковым относится, например, объем запаса на требуемое время, затраты времени на временной интервал и др.

При характеристике по показателю t выделяют неполные и полные ряды. Неполными считаются такие, в которых не соблюдается одинаковый промежуток между соседними значениями времени. Для полных, такой интервал соблюден.

Кроме этого, существует классификация по количеству показателей. Существуют изолированные – во времени анализируется всего один показатель и многомерные, когда во времени анализ ведется для целого ряда параметров, которые связаны между собой одним процессом.

Средние характеристики ряда динамики

Главный показатель, характеризующий среднее значение абсолютных показателей (y1, y2…yn) – это средний уровень ряда. Если основные интервалы не изменялись, то следует пользоваться выражением для расчета (где t – количество уровней):

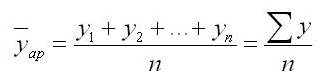
Чуть сложнее будет выглядеть методика расчета, если были временные пропуски или они неравны. Вычисления выполняются через арифметическую взвешенную:

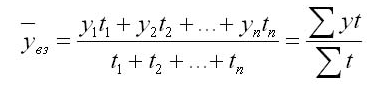
Здесь y1, y2…yn – это абсолютные уровни ряда, а t1, t2…tn – протяженности временных интервалов.

Для описания удобно пользоваться параметром среднего абсолютного прироста, представляющим собой среднее от прироста за равные временные промежутки. Когда использованы гармоничные интервалы, формула выглядит так:

Для приведенного выражения обозначение n – это число приростов за выбранный период.

Также есть методика расчетов с использованием базисного абсолютного прироста при равенстве интервалов для смыкания рядов:

Значение m – это количество уровней в выбранном периоде.

Показательная характеристика средний темп роста, он отображает как происходило изменение уровней рядя (коррелируя с единицами времени). Вычисления для цепных показателей выведены через расчет средней геометрической:

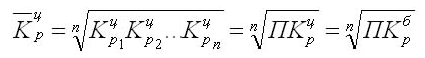
В данном выражении n количество цепных коэффициентов, Кц – сами цепные коэффициенты.

Когда даны все значения уровней, то выражение значительно упрощается:

Иногда требуется охарактеризовать срединный темп прироста, рассчитывающийся по уравнению на основании уже известных средних темпов роста (Тр):

Показатели анализа рядов динамики

Методы анализа сводятся к видоизменению полученных данных к виду, облегчающему отслеживание динамики и выявляющему ее направленность. Так или иначе придется сопоставлять уровни для понимания темпов роста / убыли.

Для оценки применяются абсолютные (вычитание уровней) и относительные (отношение уровней ряда) величины. 

Базисные показатели можно получить, если сравнивать с первым элементом. Цепные показатели – с соседними.

Это базисная и цепная абсолютные разницы соответственно.

То же в относительном выражении. В таком виде мы получим характеристику в виде коэффициента. Для более наглядного представления следует умножить на «100» и получить %%.

Надо заметить, что цепные критерии имеют свойства накапливаться и переходить в базисные:

И самые важные для оценки параметров динамики понятия — темпы:

Опять же в абсолютном и относительных видах. Если речь идет об анализе плавной кривой, то отношение заменит производная, указывающая на тангенс угла наклона касательной прямой.

Об усредненных величинах мы уже говорили. Стоит немного вернуться и рассмотреть их в связи с темпами:

Так выглядят базисный и цепной средние темпы прироста:

А вот так в относительных единицах.

Теперь на основании изложенного дополним нашу исходную таблицу и сделаем напрашивающиеся выводы.

Вполне очевидно, что отрицательные значения абсолютных величин и менее 1 относительные указывают на падение населения. При этом темпы роста ниже 0, и это указывает на сохранение неблагоприятной тенденции.

Правила построения рядов динамики

Когда производится построение временных рядов, то для них должны соблюдаться общие требования:

1. Составитель должен придерживаться принципа периодизации развития, когда разбивка на временные этапы должна быть как можно более однородной и подчиняться единому принципу развития. При этом могут использоваться методы параллельной периодизации, многомерного статистического анализа, а также исторический метод.
2. Данные, которые объединяются в многомерный временной ряд, должны обеспечивать возможность сопоставления между собой. Иными словами, должен быть определенный общий признак, например, территориальность, единицы измерения и др.
3. Временные интервалы должны быть гармонично подобраны в соответствии с вариативностью наблюдаемой характеристики. Это значит, что для величины, которая слишком часто меняет свое значение, интервал должен быть чаще, а для стабильной величины его следует сделать шире.
4. Следует соблюдать систематизацию по временной характеристике – не допускать пропуска временных точек, а если таковые возникли, то интерполировать значения внутри пропущенного интервала.

Аналитическое выравнивание ряда динамики

При определении каких-либо закономерностей во временных рядах и возможности прогнозирования отдельных тенденций, применяется методика аналитического выравнивания. С этой целью производится приближение к определенной алгебраической зависимости, наиболее точно описывающей ряд.

Методика укрупнения интервалов представляет собой преобразование, когда временные промежутки делаются более длительными, что позволяет более точно оценить общий вектор тенденции и понять, какое направление будет иметь зависимость.

Методика скользящей средней основана на особенности временных рядов погашать случайные отклонения от среднего уровня. Каждому звену с использованием простого среднеарифметичнского значения нужно рассчитывать уровень, в котором рандомные колебания сведены к минимуму.

Методика аналитического выравнивания под конкретный ряд подбирается зависимость, которая более полно отражает алгебраическую зависимость.

Примеры решения задач на тему «Ряды динамики в статистике»

Классическим упражнением является определение вида и показателей для ряда динамики.

Задача. Для указанного временного ряда высчитать: его вид, цепной и базисный прирост, темп роста/прироста, средний темп прироста.

Отчетный год	Суммарный объем производства, млрд. руб.
2014	18
2015	16
2016	17
2017	16
2018	12

Согласно определению, этот ряд динамики относится к интервальному, поскольку в условии приведен четкий промежуток времени. Произведем расчет показателей.

Абсолютные показатели

Абсолютные приросты (по цепному способу):

16 – 18 = 2 млрд. руб.

17 – 16 = 1 млрд. руб.

16 – 17 = 1 млрд. руб.

12 – 16 = 4 млрд. руб.

Абсолютные приросты (по базисному методу):

16 – 18 = -2 млрд. руб.

17 – 18 = 1 млрд. руб.

16 – 18 = -2 млрд. руб.

12 – 18 = 6 млрд. руб.

Относительные показатели

Цепные темпы роста:

16/18 х 100 = 88,8%,

17/16 х 100 = 106%,

16/17 х 100 = 94,1%,

12/16 х 100 = 75%.

Базисные темпы роста:

16/18 х 100 = 88,8%,

17/18 х 100 = 94,4%,

16/18 х 100 = 88,8%,

12/18 х 100 = 66,6%.

Цепные темпы прироста:

-2/18 х 100 = -11,1%,

1/16 х 100 = 6,25%,

-1/17 х 100 = -5,88%,

4/16 х 100 = 25%.

Базисные темпы прироста:

-2/18 х 100 = -11,1%

1/18 х 100 = 5,55%

-2/18 х 100 = -11,1%

-6/18 х 100 = -33,3%

Средний уровень временного ряда:

(18 + 16 + 17 + 16 + 12) / 5 = 15,8.

Среднегодовой абсолютный прирост:

(12 — 18) / (5 — 1) = -1,5 млрд. руб.

Среднегодовой темп прироста:

90.36 – 100 = -9.64%.

Таким образом временные ряды занимают важное место среди статистических объектов. Основное их преимущество заключается в широком практическом применении, которое позволяет использовать ряды динамики для наблюдений за физическими величинами и экономическими показателями

Важно знать о нюансах, которые помогут правильно проанализировать такие ряды

Основное их преимущество заключается в широком практическом применении, которое позволяет использовать ряды динамики для наблюдений за физическими величинами и экономическими показателями

Важно знать о нюансах, которые помогут правильно проанализировать такие ряды

Анализ сезонных колебаний

Если взять для анализа временной ряд, в котором собраны объемы продаж противовирусных препаратов за 5 лет, то будет очевидно, что ежегодно происходят колебания (снижение или увеличение) продаж, которые повторяются. Такие колебания будут именоваться сезонными.

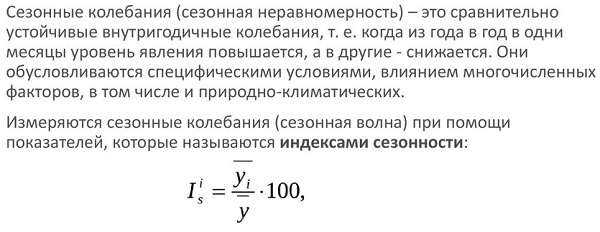
Чтобы устранить нежелательное влияние таких колебаний, проводится аналитическое изучение, выполняющееся либо с помощью гармонического исследования, либо с учетом индекса сезонности.

Индекс сезонности это фактическая характеристика того, в какое количество раз анализируемый уровень увеличен или уменьшен относительно срединного:

Тут Yt – это уровень, предполагаемый к анализу, а Ȳ это средний уровень всего ряда.

Более сложный анализ предполагает выделение гармонических колебаний. Для этого производится выравнивание по ряду Фурье (так называемые «гармоники»), и высчитывают, какие гармоники наиболее сопоставимы с анализируемым рядом. Общий вид ряда Фурье для двух гармоник выражается формулой:

Индекс сезонности

Для того чтобы не вычислять относительную разницу в процентах между каждым месяцем во временном ряду, можно вычислить один параметр – индекс сезонности.

Индекс сезонности рассчитывается на основании следующих показателей:

• среднего по анализируемому показателю в указанный временной промежуток за три и более года (yi),
• среднего значения анализируемого показателя внутри одного временного периода (года) – y.

По результатам сопоставления получается значение, которое так или иначе соотносится с уровнем в 100%. Если присутствует значимое отклонение в меньшую сторону, то это является свидетельством присутствия сезонного колебания.

Понятие о рядах динамики

Строгое понятие для ряда динамики обозначено в статистике так.

Динамические ряды (иными словами ряд динамики или временной ряд) – это распределенные в увеличивающемся порядке дискретных значений выбранного статистического параметра за последовательные временные промежутки.

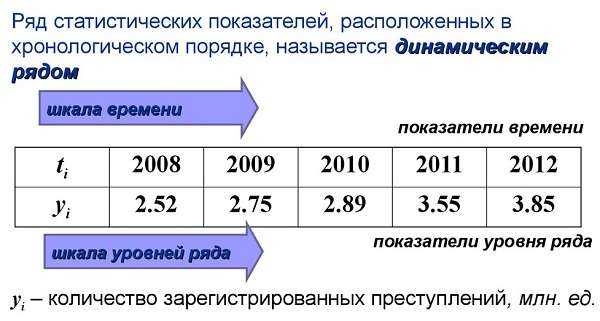
Если рассмотреть динамический ряд, будет очевидно, что он наполнен данными в формате y1t1, y2t2, y3t3…yntn. Применительно к временному ряду, значением у будет называться «уровень ряда», при этом первый член ряда (у1) называется базисным (начальным) уровнем, а уn – конечным уровнем. Через обозначение t будет обозначаться временной показатель, который соответствует каждому из уровней ряда.

При построении графической зависимости временного ряда, функция будет иметь вид t(y), где по оси y (ординат) будут отложены значения уровней ряда (параметр у), а по оси х (ось абсцисс) будут отложены временные значения параметра t.

Показатели анализа рядов динамики

Всего имеются 5 характеристик, предназначающихся для выполнения анализа:

абсолютный прирост – это параметр, получающийся при нахождении разности определенного уровня и базисного (или тем, который следует до него). Возможен ответ со знаком «-». Выражения для расчета выглядят так:

коэффициент роста – значение, которое характеризует, в какое количество раз увеличился (или снизился) конкретно взятый для анализа уровень по сравнению с базисным или любым другим (например, идущим перед выбранным). Формула сводится к делению значения анализируемого уровня на значение базисного (отношение уровней):

• темп роста – характеризует процентное соотношение анализируемого показателя в сопоставлении с базисным. Вычисления выполняются перемножением значения коэффициента роста на сто процентов,
• темп прироста – процентный порог возрастания или снижения значения уровня в сопоставлении с базисным. При обсчете необходимо из 100 вычесть показатель темпа роста,
• абсолютное значение 1% прироста будет получено при делении абсолютного прироста на темп прироста. Эти характеристики не относятся к обязательным элементам.

Виды рядов динамики в статистике

Разделяют последовательности по временным показателям и по представлению чисел:

1. Отсечка производится по конкретному отрезку времени (моментный ряд) или суммируется за какой-то промежуток (интервальный ряд). В приведенном примере – первый случай. Показано состояние на определенную дату. Попытка что-то просуммировать даст бессмысленное число. Второй способ актуален, если, например, характеризуется выпуск товаров за неделю, месяц, квартал.

2. С постоянным или изменяющимся временным отрезком. В нашем случае отображаются регулярные годовые замеры.

3. Показаны абсолютные, средние или относительные безразмерные числа. У нас иллюстрируется количество живущих в государстве людей без каких-либо алгебраических вмешательств.

4. По сути показателей. Может сопоставляться курс валюты (одномерный критерий), а может состоять из объемов закупки разных валют (многомерный). В примере фигурирует только одна величина.

Расчеты среднего уровня в рядах динамики

Существуют случаи, когда требуются какие-то резюмирующие значения. Среднее – из таких. При этом методики его определения для разных видов рядов отличаются.

Интервальный ряд динамики

В этом случае требуется просто поиск среднего арифметического. Таким образом можно показать какие-то сезонные колебания производства, продаж.

Рассчитать можно по формуле:

где Y – уровни;

n – их количество.

В нашем случае подобная цифирь полезной нагрузки не несет, только для наглядности:

(144,2 + … + 141,9) / 6 = 866,6 / 6 = 142,77.

Таково среднее население за 5 лет.

Моментный ряд динамики

Если разрыв в датах неизменен, то можно записать последовательность в средних значениях. Получим (n – 1) чисел такого вида

После нехитрых выкладок обнаруживаем, что

y(1), y(n) – базисный и конечный уровни;

y(i) – внутренние.

Считаем:

((141.2 + 141,9) / 2 + 143,5 + … + 142) / 5 = (143,05 + 570,5) / 2 = 142,71.

Мы получили среднее хронологическое.

Но это для равных отрезков. Когда они меняются, необходимо учитывать временной фактор. Если уровни меняются с течением времени, то выводится такое:

Выражение несколько упрощается, если уровни постоянны до следующей отсечки.

t(i) – длительность периода, когда уровень i зафиксирован.