Средние величины и показатели вариации

Виды средних величин, используемых в статистике

Рассмотрим основные виды средних величин, используемых при решении социально-эконмических и аналитических задач.

Средняя арифметическая простая вычисляется по формуле:

Средняя арифметическая простая используется в тех случаях, когда расчет осуществляется по не сгруппированным
данным. Пример применения формулы средней арифметической простой представлен в задаче 1.

Средняя арифметическая взвешенная определяется по формуле:

При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по несколько раз.
В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам. Пример применения формулы средней
арифметической взвешенной представлен в задаче 2.

Средняя гармоническая простая определяется по формуле:

Средние гармонические используются тогда, когда по экономическому содержанию имеется информация для числителя, а для
знаменателя ее необходимо предварительно определить.

Средняя гармоническая взвешенная определяется по формуле:

Данная формула используется для расчета средних показателей не только в статике, но и в динамике, когда известны
индивидуальные значения признака и веса W за ряд временных интервалов. Пример применения формулы средней гармонической взвешенной
представлен в задаче 3.

Средняя геометрическая простая (невзвешенная) опеределяется по формуле:

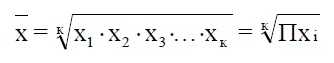Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста.

Средняя квадратическая простая (невзвешенная) опеределяется по формуле:

Средняя квадратическая лежит в основе вычислений ряда сводных расчетных показателей.

Наиболее часто используемыми в экономической практике структурными средними
являются мода и медиана.
Мода (Мо) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой.
Медианой (Ме) называется значение признака, приходящееся на середину ранжированной (упорядоченной)
совокупности. Пример определения медианы и моды для дискретного ряда чисел представлен в задаче 1.

Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака
от медианы меньше, чем от любой другой величины.

Для интервального
ряда расчет моды осуществляется по формуле:

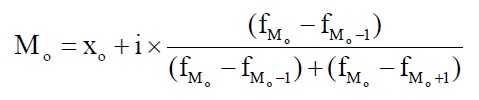где Хо — нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту);
i — величина модального интервала; f Мо — частота модального интервала; f Мо-1 — частота интервала,
предшествующего модальному; f Мо+1 — частота интервала, следующего за модальным.

Для интервального
ряда расчет медианы осуществляется по формуле:

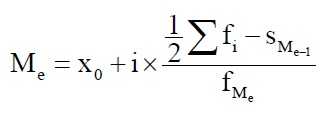Хо — нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота
которого превышает половину общей суммы частот); i — величина медианного интервала; Sme-1 — накопленная
частота интервала, предшествующего медианному; f Me — частота медианного интервала.

Формула среднего значения в Excel

Среднее арифметическое чисел в Excel рассчитывают с помощью функции СРЗНАЧ. Выглядит примерно так.

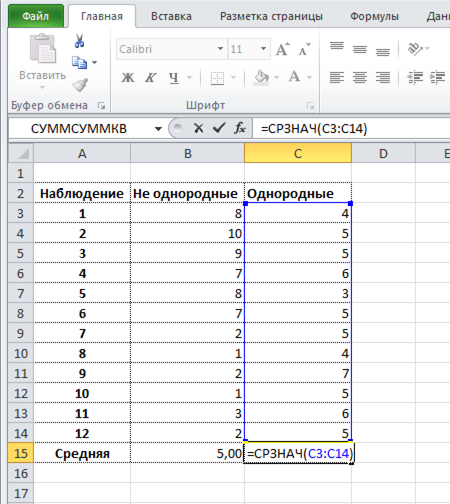
У этой формулы есть замечательное свойство. Если в диапазоне, по которому рассчитывается формула, присутствуют пустые ячейки (не нулевые, а именно пустые), то они исключается из расчета.

Вызвать функцию можно разными способами. Например, воспользоваться командой автосуммы во вкладке Главная:

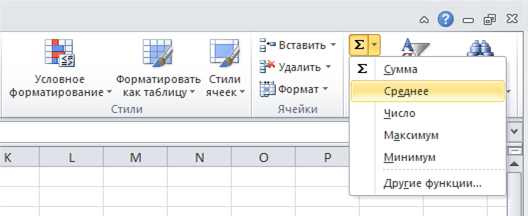
После вызова формулы нужно указать диапазон данных, по которому рассчитывается среднее значение.

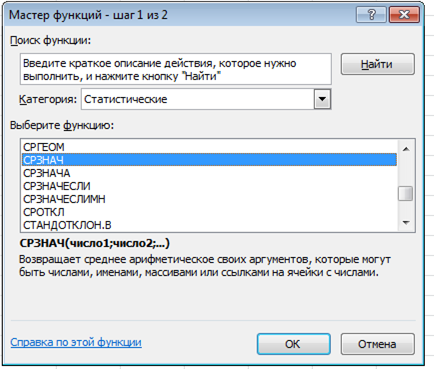
Есть и стандартный способ для всех функций. Нужно нажать на кнопку fx в начале строки формул. Затем либо с помощью поиска, либо просто по списку выбрать функцию СРЗНАЧ (в категории «Статистические»).

Среднее арифметическое

Среднее арифметическое знакомо нам всем со школы:

среднее арифметическое = сумма всех величин/количество величин

Задачка: вы весите 75 кг и зашли в лифт с подростком весом 50 кг и толстяком весом 175 кг. Каков средний вес вашей группы?

На самом деле вопрос стоит так: Если заменить вашу весёлую компанию тремя клонированными людьми с одинаковым весом, каким весом должен обладать каждый такой клон?

В этом случае мы просто заказываем на фабрике по производству клонов человека трёх экземпляров весом в 100 килограмм каждый (Помним: (75+50+175)/3) и довольно потираем руки.

Преимущества среднего арифметического:

Отлично работает для совокупностей, значения которых легко складываются;
Просто вычисляется: складывай, разделяй и властвуй;
Интуитивно понятно — среднее арифметическое для нас как раз и является «числом где-то в середине» между наибольшим и наименьшим значением.

Недостатки среднего арифметического:

Среднее арифметическое не работает для числовых рядов с большим разбросом в значениях. Ну, скажем, среднее арифметическое чисел 100, 200 и -300 — это 0, а это уже обескураживает.

Среднее арифметическое срабатывает в 80% случаев. К сожалению, 20% оставшихся случаев и вынуждают нас искать альтернативы для подсчёта среднего значения.

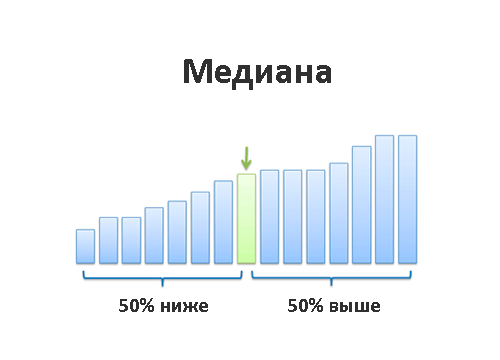
Медиана

Медиана — это та самая грань, которая отделяет наибольшие значения от наименьших. То самое «число посередине». Постойте-постойте, а разве среднее арифметическое делает не то же самое?

Вот вам простой пример. Какое число находится в середине этого ряда?

1, 2, 3, 4, 100

Число «3» находится в середине ряда. И хотя среднее арифметическое (22) является «средним», оно никак не отражает распределения этих чисел. Интуитивно (и абсолютно правильно!) мы считаем, что в середине этого ряда всё-таки 3, а не 22. Здесь среднее значение увеличилось благодаря резко отклоняющемуся от общей массы значению, 100.

Медиана решает эту проблему. Медиана делит наш числовой ряд на две равные части, причём первая половина имеет значения меньше либо равные медиане, а вторая — больше либо равные. Если в середине числового ряда оказывается два числа, мы просто берём среднее арифметическое этих двух чисел, чтобы получить медиану. В числовом ряду 1, 2, 3, 4 медианой станет число 2,5. Именно медиана позволяет выбивающимся из общей массы числам вроде 100 в нашем примере выше не влиять на общее впечатление о числовом ряде.

Преимущества медианы:

Прекрасно справляется с резко отклоняющимися значениями, поэтому зачастую является самым репрезентативным значением для группы;
Разбивает данные на две группы, состоящие из одинакового количества элементов.

Недостатки медианы:

Немного усложняются вычисления: необходимо разбить ряд на две части;
Медиана менее популярна; если вы скажете «среднее медианное значение», люди запросто могут подумать, что вы говорите о среднем арифметическом. Отсюда возникают недопонимания.

Такие средние значения, как цены на недвижимость или, например, уровень дохода часто вычисляются именно по медиане, потому что нам важна именно средняя стоимость большей части домов в конкретном районе или средний уровень доходов большей части населения. В таком случае Билл Гейтс с годовым доходом в несколько миллиардов не испортит нам всю статистику. Видите, как много зависит от того, как мы работаем с имеющимися данными?

Среднее гармоническое

Среднее гармоническое представить сложнее, чем предыдущих представителей «средних», но оно не менее полезно. Между прочим, само понятие «гармоники» в математике связано с обратными числами (1/2, 1/3 и т.д.). Среднее гармоническое помогает нам вычислить среднее арифметическое в рядах чисел, заданных обратными значениями. Это случается чаще, чем вы можете подумать.

Например, если я еду со скоростью 30 км/ч, это значит, что я получаю определённый результат (30 км) за какую-либо единицу времени (1 час). Когда мы хотим узнать среднее значение для нескольких скоростей (Х и Y), нужно думать о результате и единицах измерения, а не об исходных цифрах.

средняя скорость = общий результат/общая единица измерения

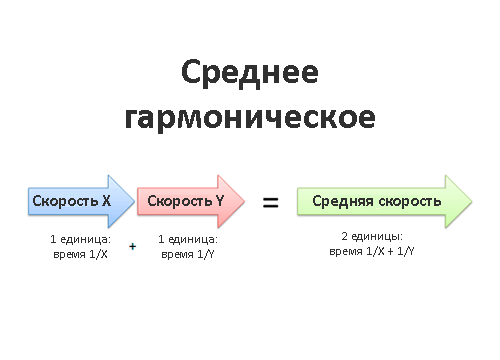
Возьмём двух работников: Х и Y. Оба работают в одном проекте и выполняют одинаковое количество работы, но скорость их работы разная. Какова средняя скорость их работы?

Скажем, работник Х кладёт 30 кирпичей в час, а работник Y — 60 кирпичей в час. Значит, на один кирпич у каждого работника уходит:

У работника X укладка одного кирпича займёт 1/X времени (1/30);
У работника Y укладка одного кирпича займёт 1/Y времени (1/60)

Складываем результаты и единицы измерения:

Общий результат: 2 кирпича (Х и Y уложили по одному) Общая единица времени: 1/X + 1/Y (у каждого уходит разное количество времени)

Средней скоростью обоих работников будет:

Если бы у нас было 3 работника (X, Y и Z), их средняя скорость вычислялась бы по формуле:

Здорово же иметь одну формулу вместо того, чтобы каждый раз заниматься долгими вычислениями. Даже вычисляя среднюю скорость 5 нерадивых работников стало бы головной болью. Помните наш первый пример про скорость, с которой вы едете на работу и домой? Чтобы найти среднюю скорость вашего передвижения в тот день, мы просто используем формулу.

При этом нам даже не нужно знать, где находится дом или офис! Теперь вместо X и Y у нас не кирпичи, а количество километров за единицу времени. Вне зависимости от расстояния результат один и тот же: допустим, некое количество километров R мы проходим на скорости X, а другое количество километров R — на скорости Y. Средняя скорость при этом будет вычисляться так же, как вычисляется средняя скорость прохождения 1 км на скорости X и одного километра на скорости Y:

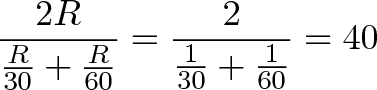
Ключевая идея: Среднее гармоническое используется тогда, когда один и тот же объём работы выполняется на разных скоростях.

Ещё более ключевая идея: Помните, что среднее значение — это один элемент, способный передать суть целой группы элементов. В нашем примере с работой и офисой в среднем туда-обратно мы едем на скорости 40 км/ч (вместо 30 км/ч туда и 60 км/ч обратно)

Важно помнить, что средней скоростью мы заменяем каждую «стадию»

Ещё несколько примеров из жизни среднего гармонического:

Передача данных: Мы передаём данные между клиентом и сервером. Клиент посылает данные за плату 10 Гб/доллар, а сервер получает их за плату 20 Гб/доллар. Каково среднее количество Гб, которые можно передать и получить за один доллар? Мы усредняем значения для клиента и для сервера: 2 / (1/10 + 1/20) = 13,3 Гб/доллар для каждой стороны. Поскольку данные и передаются, и получаются (каждая сторона выполняет свою половину работу), мы делим это значение на 2 и получаем следующее значение: 6,65 Гб за доллар.
Продуктивность машины: У нас есть производственная установка для подготовки и полировки деталей. За час установка может подготовить 25 деталей; либо за тот же час она может отполировать 10 деталей. Какова средняя производительность установки? Усредняем значения для каждой стадии: 2 / (1/25 + 1/10) = 14,28 деталей/час. Снова делим это значение на два, поскольку нас интересует средняя производительность установки, если она занимается сразу двумя фазами: получаем 7,14 деталей/час.

Средняя арифметическая как оценка математического ожидания

Теория вероятностей занимается изучением случайных величин. Для этого строятся различные характеристики, описывающие их поведение. Одной из основных характеристик случайной величины является математическое ожидание, являющееся своего рода центром, вокруг которого группируются остальные значения.

Формула матожидания имеет следующий вид:

где M(X) – математическое ожидание

x_i – это случайные величины

p_i – их вероятности.

То есть, математическое ожидание случайной величины — это взвешенная сумма значений случайной величины, где веса равны соответствующим вероятностям.

Математическое ожидание суммы выпавших очков при бросании двух игральных костей равно 7. Это легко подсчитать, зная вероятности. А как рассчитать матожидание, если вероятности не известны? Есть только результат наблюдений. В дело вступает статистика, которая позволяет получить приблизительное значение матожидания по фактическим данным наблюдений.

Математическая статистика предоставляет несколько вариантов оценки математического ожидания. Основное среди них – среднее арифметическое.

Среднее арифметическое значение рассчитывается по формуле, которая известна любому школьнику.

где x_i – значения переменной,n – количество значений.

Среднее арифметическое – это соотношение суммы значений некоторого показателя с количеством таких значений (наблюдений).

Мода

Само слово может звучать странно, но оно означает всего лишь наиболее часто встречающийся в группе элемент. На практике обычно мода определяется путём опросов и сбора мнений. Да, действительно порой бывают случаи, когда лучшим способом получить наиболее репрезентативный образец данных является сбор откликов.

Ну, скажем, вы планируете вечеринку, и вам нужно выбрать день для её проведения. Дни недели — такой же числовой ряд, что и любой другой. Это всего лишь числа от 1 до 7. Среднее арифметическое и медиана тут не помогут (Лиза и Паша могут в пятницу, а Коля и Петя — в воскресенье; поэтому назначим субботу). Что делать в таком случае? Конечно, выбрать тот день, который выберет большинство.

Как правило, мода используется для получения наиболее репрезентативного значения в нечисловых рядах. Популярные цвета в сезоне, хиты продаж, рейтинги фильмов и музыки, лучшие кафе и закусочные определяются именно по моде.

Преимущества моды: — Прекрасно работает для получения представления об общественном мнении; — Даёт представление о потребностях большой части людей (там, где среднее арифметическое даёт лишь осечку); — Проста для понимания.

Недостатки моды: — Для её вычисления требуется больше усилий (нужно собрать мнения и обработать их); — Победителю достаётся всё: мода выявляет только одного лидера.

Физический смысл средней арифметической

Представим, что имеется спица, на которой в разных местах нанизаны грузики различной массы.

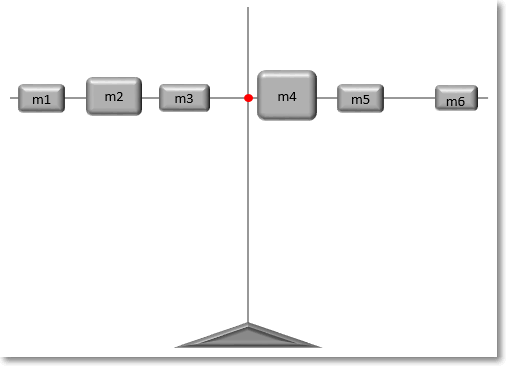
Как отыскать центр тяжести? Центр тяжести – это такая точка, за которую можно ухватиться, и спица при этом останется в горизонтальном положении и не будет переворачиваться под действием силы тяжести. Она должна быть в центре всех масс, чтобы силы слева равнялись силам справа. Для нахождения точки равновесия следует рассчитать среднее арифметическое взвешенное расстояний от начала спицы до каждого грузика. Весами будут являться массы грузиков (m_i), что в прямом смысле слова соответствует понятию веса. Таким образом, среднее арифметическое расстояние – это центр равновесия системы, когда силы с одной стороны точки уравновешивают силы с другой стороны.

И последнее. В русском языке так сложилось, что под словом «средний» обычно понимают именно среднее арифметическое. То есть моду и медиану как-то не принято называть средним значением. А вот на английском языке слово «средний» (average) может трактоваться и как среднее арифметическое (mean), и как мода (mode), и как медиана (median). Так что при чтении иностранной литературы следует быть бдительным.

Другие статьи по данной теме:

назад: Абсолютные и относительные величины в статистике. Примеры решения задач
далее: Показатели вариации: понятие, виды, формулы для вычислений.
Примеры решения задач

Список использованных источников

Белобородова С.С. и др. Теория статистики: Типовые задачи с контрольными заданиями.
Екатеринбург: Изд-во Урал. гос. экон. ун-та, 2001;
Минашкин В.Г. и др. Курс лекций по теории статистики. / Московский международный институт эконометрики,
информатики, финансов и права. — М., 2003;
Сизова Т.М. Статистика: Учебное пособие. – СПб.: СПб ГУИТМО, 2005;
Фёдорова Л.Н., Фёдорова А.Е. Методические указания по написанию контрольной работы по курсу «Статистика»
для студентов экономических специальностей: УрГЭУ, 2007;

Но что всё это значит?

Давайте начнём сначала. Что вообще мы понимаем под словом «среднее»? Для большинства из нас это «какое-то число посередине» либо некое сбалансированное по каким-то критериям число.

Можно предложить более универсальную интерпретацию понятия «среднее значение». Среднее значение какого-либо ряда значений — это то, которым можно заменить любую единицу ряда и получить тот же результат. Условно говоря, я могу выбросить все представленные данные, кроме среднего значения, и общий смысл не изменится.

Одна из целей получения среднего значения — это понять суть выборки данных с помощью репрезентативного образца. Но сам процесс вычисления среднего значения зависит от того, каким образом взаимодействуют элементы группы данных. Давайте посмотрим, как это происходит.

Средняя арифметическая взвешенная

Рассмотрим следующую простую задачу. Между пунктами А и Б расстояние S, которые автомобиль проехал со скоростью 50 км/ч. В обратную сторону – со скоростью 100 км/ч.

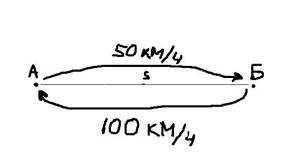
Какова была средняя скорость движения из А в Б и обратно? Большинство людей ответят 75 км/ч (среднее из 50 и 100) и это неправильный ответ. Средняя скорость – это все пройденное расстояние, деленное на все потраченное время. В нашем случае все расстояние – это S + S = 2*S (туда и обратно), все время складывается из времени из А в Б и из Б в А. Зная скорость и расстояние, время найти элементарно. Исходная формула для нахождения средней скорости имеет вид:

Теперь преобразуем формулу до удобного вида.

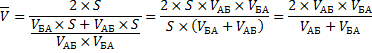
Подставим значения.

Правильный ответ: средняя скорость автомобиля составила 66,7 км/ч.

Средняя скорость – это на самом деле среднее расстояние в единицу времени. Поэтому для расчета средней скорости (среднего расстояния в единицу времени) используется средняя арифметическая взвешенная по следующей формуле.

где x – анализируемый показатель; f – вес.

Аналогичным образом по формуле средневзвешенной средней рассчитывается средняя цена (средняя стоимость на единицу продукции), средний процент и т.д. То есть если средняя считается по другим усредненным значениям, нужно применить среднюю взвешенную, а не простую.

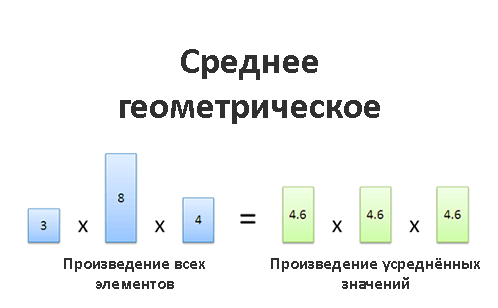
Среднее геометрическое

Наш «усреднённый элемент» зависит от того, что мы делаем с уже существующими элементами группы данных. В большинстве случаев элементы просто складываются, и среднее арифметическое прекрасно работает. Но иногда нам нужно что-то большее. Например, когда мы работаем с инвестициями, площадью и объёмом. В таких случаях данные взаимодействуют между собой именно путём умножения (ожидаемая доходность, объём или площадь фигуры вычисляются с помощью умножения), и это меняет наш подход к выявлению средних значений.

Вот пример. Какой инвестиционный портфель вы предпочтёте? Иными словами, какой из них принесёт большую прибыль в течение типичного года?

Портфель А: +10%, -10%, +10%, -10%
Портфель Б: +30%, -30%, +30%, -30%

Выглядят они похоже. Наша повседневная логика, построенная на привычке к среднему арифметическому, говорит нам, что оба портфеля достаточно рискованны, и оба в среднем приведут к убыткам или нулевой прибыли. Поэтому, наверное, мы выберем портфель Б, поскольку в успешный год он принесёт больше прибыли.

И это неверно! На фондовом рынке с таким подходом мы с вами точно бы прогорели. Проценты с инвестиций умножаются, а не складываются. Мы не можем просто взять и использовать среднее арифметическое, нам нужно найти действительный коэффициент окупаемости. Коэффициент окупаемости считается достаточно просто: берём условные 100% нашего текущего капитала в качестве единицы. Далее представляем колебания доходности-убытка, представленные в описании портфелей, добавляя к нашей единице или вычитая из неё процентные показатели. Затем перемножаем полученные колебания и получаем коэффициент. Для расчёта среднегодового значения коэффициента окупаемости делим полученный коэффициент на 4 (поскольку элементов в нашем числовом ряду четыре).

Портфель А:

Коэффициент окупаемости: 1,1 * 0,9 * 1,1 * 0,9 = 0,98 (2% убытка)

Среднегодовое значение: (0,98)^(1/4) = 0,5% годового убытка

Портфель Б:

Коэффициент окупаемости: 1,3 * 0,7 * 1,3 * 0,7 = 0,83 (17% убытка)

Среднегодовое значение: (0,83)^(1/4) = 4,6% годового убытка

Выбор между 2% или 17%? Огромная разница! Конечно, разумный человек отказался бы от обоих портфелей, но из двух зол лучше выбрать Портфель А. И именно здесь среднее арифметическое не работает.

Несколько примеров, где работает среднее геометрическое:

Темпы инфляции: У вас есть показатели в 1%, 2% и 10%. Каков средний показатель инфляции за конкретный период времени? (1,01 * 1,02 * 1,10)^(1/3) = 4,3%.
Скидки: У вас есть три скидочных купона на 50%, 25% и 35%. Какова средняя скидка? (0,5 * 0,75 * 0,65)^(1/3) = 37.5%.
Площадь: У вас есть участок земли 40х60 м. Вам нужно вычислить «усреднённую сторону» — иными словами, сторону квадрата примерно той же площади. (40 * 60)^(0.5) = 49 м.
Объём: У вас есть коробка 12х24х48 см. Вам снова нужна усреднённая сторона, то есть сторона куба примерно того же объёма. (12 * 24 * 48)^(1/3) = 24 см.

Среднее геометрическое помогает найти «типичный элемент» среди группы элементов, взаимодействующих друг с другом путём умножения. И, как видим, у него множество практических применений.

Свойства средней арифметической (математического ожидания)

Теперь рассмотрим свойства средней арифметической, которые часто используются при алгебраических манипуляциях. Правильней будет вновь вернутся к термину математического ожидания, т.к. именно его свойства приводят в учебниках.

Матожидание в русскоязычной литературе обычно обозначают как M(X), в иностранных учебниках можно увидеть E(X). Встречается обозначение греческой буквой μ (читается «мю»). Для удобства предлагаю вариант M(X).

Итак, свойство 1. Если имеются переменные X, Y, Z, то математическое ожидание их суммы равно сумме их математических ожиданий.

M(X+Y+Z) = M(X) + M(Y) + M(Z)

Допустим, среднее время, затрачиваемое на мойку автомобиля M(X) равно 20 минут, а на подкачку колес M(Y) – 5 минут. Тогда общее среднее арифметическое время на мойку и подкачку составит M(X+Y) = M(X) + M(Y) = 20 + 5 = 25 минут.

Свойство 2. Если переменную (т.е. каждое значение переменной) умножить на постоянную величину (a), то математическое ожидание такой величины равно произведению матожидания переменной и этой константы.

M(aX) = aM(X)

К примеру, среднее время мойки одной машины M(X) 20 минут. Тогда среднее время мойки двух машин составит M(aX) = aM(X) = 2*20 = 40 минут.

Свойство 3. Математическое ожидание постоянной величины (а) есть сама эта величина (а).

M(a) = a

Если установленная стоимость мойки легкового автомобиля равна 100 рублей, то средняя стоимость мойки нескольких автомобилей также равна 100 рублей.

Свойство 4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий.

M(XY) = M(X)M(Y)

Автомойка за день в среднем обслуживает 50 автомобилей (X). Средний чек – 100 рублей (Y). Тогда средняя выручка автомойки в день M(XY) равна произведению среднего количества M(X) на средний тариф M(Y), т.е. 50*100 = 500 рублей.

Формула средневзвешенного значение в Excel

Обычная функция среднего значения в Excel СРЗНАЧ, к сожалению, считает только среднюю простую. Готовой формулы для среднего взвешенного значения в Excel нет. Однако расчет несложно сделать подручными средствами.

Самый понятный вариант создать дополнительный столбец. Выглядит примерно так.

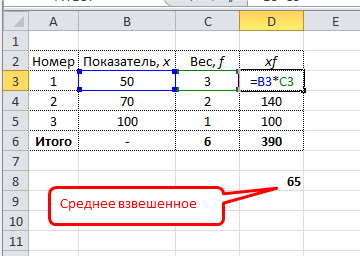
Имеется возможность сократить количество расчетов. Есть функция СУММПРОИЗВ. С ее помощью можно рассчитать числитель одним действием. Разделить на сумму весов можно в этой же ячейке. Вся формула для расчета среднего взвешенного значения в Excel выглядит так:

=СУММПРОИЗВ(B3:B5;C3:C5)/СУММ(C3:C5)

Интерпретация средней взвешенной такая же, как и у средней простой. Средняя простая – это частный случай взвешенной, когда все веса равны 1.