§ 1.19. потенциал электростатического поля и разность потенциалов

Потенциальность электростатического поля

Электрическое поле с напряженностью $ \vec{E} $ при перемещении заряда $ q $ совершает работу. Работа $ A $ электростатического поля вычисляется по формуле:

где $ d $ – расстояние, на которое перемещается заряд,
$ \alpha $ – угол между векторами напряженности электрического поля и перемещения заряда.

Важно!
Эта формула применима для нахождения работы только в однородном электростатическом поле. Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только начальным и конечным положением заряда

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только начальным и конечным положением заряда.

Потенциальным называется поле, работа сил которого по перемещению заряда по замкнутой траектории равна нулю.

Важно!
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Электростатическое поле является потенциальным

Работа электростатического поля по перемещению заряда равна изменению потенциальной энергии, взятому с противоположным знаком. В электродинамике энергию принято обозначать буквой $ W $, так как буквой $ E $ обозначают напряженность поля:

Потенциальная энергия заряда $ q $, помещенного в электростатическое поле, пропорциональна величине этого заряда. Потенциальная энергия взаимодействия зарядов вычисляется относительно нулевого уровня (аналогично потенциальной энергии поля силы тяжести). Выбор нулевого уровня потенциальной энергии определяется исходя из соображений удобства при решении задачи.

Эквипотенциальные поверхности

Если потенциал нескольких точек одинаков, и эти точки образуют поверхность, то такая поверхность называется эквипотенциальной. Таким свойством обладает, например, сфера, описанная вокруг электрического заряда, ведь электрическое поле убывает с расстоянием одинаково во все стороны.

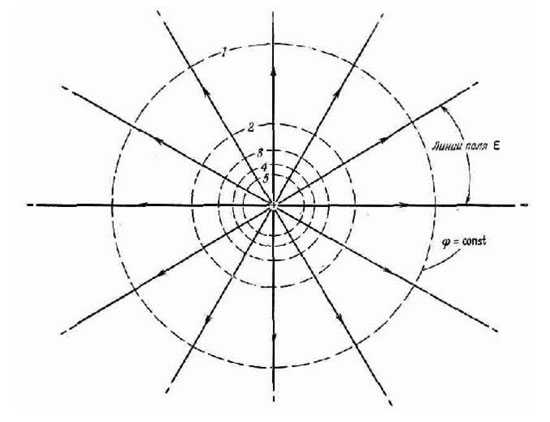
Все точки этой поверхности имеют одинаковую потенциальную энергию, поэтому при перемещении заряда по такой сфере работа затрачиваться не будет. Эквипотенциальные поверхности систем из нескольких зарядов имеют более сложную форму, но у них есть одно интересное свойство – они никогда не пересекаются. Силовые линии электрического поля всегда перпендикулярны поверхностям с одинаковым потенциалом в каждой их точке. Если эквипотенциальную поверхность рассечь плоскостью, получится линия равных потенциалов. Она имеет те же свойства, что и эквипотенциальная поверхность. На практике равный потенциал имеют, например, точки на поверхности проводника, помещенного в электростатическое поле.

Разобравшись с понятием потенциала и разности потенциалов, можно приступать к дальнейшему изучению электрических явлений. Но не ранее, потому что без понимания базовых принципов и понятий углубить знания не получится.

Магнитное поле: источники, свойства, характеристики и применение

Чем отличаются и где используются постоянный и переменный ток

Что такое электрический ток простыми словами

Сила Лоренца и правило левой руки. Движение заряженных частиц в магнитном поле

Что такое датчик Холла: принцип работы, устройство и способы проверки на работоспособность

Проверка электрических параметров автомобильного аккумулятора с помощью мультиметра

Что такое электрический потенциал

Пусть в поле, создаваемым неподвижным зарядом Q, помещён единичный заряд q, на который действует сила Кулона F=k*Qq/r.

Внесённый заряд под действием этой силы может перемещаться, а сила при этом совершит определенную работу. Это означает, что система из двух зарядов обладает потенциальной энергией, зависящей от величины обоих зарядов и расстояния между ними, причём величина этой потенциальной энергии не зависит от величины заряда q. Здесь и вводится определение электрического потенциала – он равен отношению потенциальной энергии поля к величине заряда:

φ=W/q,

где W – потенциальная энергия поля, создаваемого системой зарядов, а потенциал является энергетической характеристикой поля. Чтобы переместить заряд q в электрическом поле на какое-то расстояние, надо затратить определённую работу на преодоление кулоновских сил. Потенциал точки равен работе, которую надо затратить для перемещения единичного заряда из этой точки в бесконечность. При этом надо отметить, что:

эта работа будет равна убыли потенциальной энергии заряда (A=W₂-W₁);
работа не зависит от траектории перемещения заряда.

В системе СИ единицей измерения потенциала является один Вольт (в русскоязычной литературе обозначается буквой В, в зарубежной – V). 1 В=1Дж/1 Кл, то есть, можно говорить о потенциале точки в 1 вольт, если для перемещения заряда в 1 Кл в бесконечность потребуется совершить работу в 1 Джоуль. Название выбрано в честь итальянского физика Алессандро Вольта, внесшего значительный вклад в развитие электротехники.

Чтобы наглядно представить, что такое потенциал, его можно сравнить с температурой двух тел или температурой, замеренной в разных точках пространства. Температура служит мерой нагрева объектов, а потенциал – мерой электрической заряженности. Говорят, что одно тело нагрето более другого, также можно сказать, что одно тело заряжено более, а другое – менее. Эти тела обладают разным потенциалом.

Значение потенциала зависит от выбора системы координат, поэтому требуется какой-то уровень, который надо принять за ноль. При измерении температуры за базовую границу можно принять, например, температуру тающего льда. Для потенциала за нулевой уровень обычно принимают потенциал бесконечно удаленной точки, но для решения некоторых задач за нулем можно считать, например, потенциал земли или потенциал одной из обкладок конденсатора.

Свойства потенциала

Среди важных свойств потенциала надо отметить следующие:

если поле создается несколькими зарядами, то потенциал в конкретной точке будет равен алгебраической (с учетом знака заряда) сумме потенциалов, создаваемых каждым из зарядов φ=φ₁+φ₂+φ₃+φ₄+φ₅+…+φ_n;
если расстояния от зарядов таковы, что сами заряды можно считать точечными, то суммарный потенциал считается по формуле φ=k*(q₁/r₁+q₂/r₂+q₃/r₃+…+q_n/r_n), где r – расстояние от соответствующего заряда то рассматриваемой точки.

Если поле образовано электрическим диполем (двумя связанными зарядами противоположного знака), то потенциал в любой точке, находящейся на расстоянии r от диполя будет равен φ=k*p*cosά/r2, где:

p – электрическое плечо диполя, равное q*l, где l – расстояние между зарядами;
r – расстояние до диполя;
ά – угол между плечом диполя и радиус-вектором r.

Если точка лежит на оси диполя, то cosά=1 и φ=k*p/r2.

Действие электрического поля на электрические заряды

Электрическое поле – это особая форма материи, существующая вокруг электрически заряженных тел.

Впервые понятие электрического поля было введено Фарадеем. Он объяснял взаимодействие зарядов следующим образом: каждый заряд создает вокруг себя электрическое поле, которое с некоторой силой действует на другой заряд.

Свойства электрического поля заключаются в том, что оно:

материально;
создается зарядом;
обнаруживается по действию на заряд;
непрерывно распределено в пространстве;
ослабевает с увеличением расстояния от заряда.

Действие заряженного тела на окружающие тела проявляется в виде сил притяжения и отталкивания, стремящихся поворачивать и перемещать эти тела по отношению к заряженному телу.

Силу, с которой электрическое поле действует на заряд, можно рассчитать по формуле:

где $ \vec{E} $ – напряженность электрического поля, $ q $ – заряд.

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов механики с учетом закона Кулона и вытекающих из него следствий.

Алгоритм решения задач о точечных зарядах и системах, сводящихся к ним:

сделать рисунок; указать силы, действующие на точечный заряд, помещенный в электрическое поле;
записать для заряда условие равновесия или основное уравнение динамики материальной точки;
выразить силы электрического взаимодействия через заряды и поля и подставить эти выражения в исходное уравнение;
если при взаимодействии заряженных тел между ними происходит перераспределение зарядов, к составленному уравнению добавить уравнение закона сохранения зарядов;
записать математически все вспомогательные условия;
решить полученную систему уравнений относительно неизвестной величины;
проверить решение

Потенциал. Разность потенциалов. ЗАДАЧИ с решениями

Формулы, используемые на уроках «Решение задач на тему: Работа перемещения заряда в электрическом поле. Потенциал. Разность потенциалов» для подготовки к ЕГЭ.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
Металлический шар диаметром d заряжен с поверхностной плотностью зарядов σ. Найти потенциал φ этого шара, если он окружен заземленной проводящей сферой, имеющей общий с шаром центр. Диаметр сферы D. Среда — воздух.

Задача № 2.
Потенциал заряженного шара φ₁ = 300 В. Чему равен потенциал φ₂ электрического поля этого шара в точке, отстоящей на расстоянии l = 50 см от его поверхности, если радиус шара R = 25 см?

Задача № 3.
Определить потенциал φ точки поля, находящейся на расстоянии а = 9 см от поверхности заряженного шара радиусом R = 1 см, если поверхностная плотность зарядов на шаре σ = 1 • 10–11 Кл/см2. Среда — воздух.

Задача № 4.
В точке 1 поля точечного заряда-источника потенциал φ₁ = 40 В, а в точке 2 φ₂ = 10 В. Найти потенциал φ в точке М, лежащей посередине между точками 1 и 2 (рис. 3-6).

Задача № 5.
В трех вершинах квадрата со стороной а = 20 см находятся заряды q₁ = 1 • 10–8 Кл, q₂ = 2 • 10–8 Кл и q₃ = 2 • 10–8 Кл (рис. 3-7). Определить потенциал φ электрического поля, созданного этими зарядами в четвертой вершине.

Задача № 6.
Четыре одинаковых точечных заряда q расположены на одной прямой на расстоянии r друг от друга. Какую работу А надо совершить, чтобы переместить эти заряды в вершины тетраэдра со стороной r? Среда — вакуум.

Задача № 7.
Два одинаково заряженных шарика диаметрами d = 0,5 см каждый расположены на расстоянии l = 2 см между их поверхностями (рис. 3-14). До какого потенциала φ они заряжены, если сила их отталкивания друг от друга F = 2 мкН? Среда — воздух.

Задача № 8.
В однородном электрическом поле напряженностью Е = 2 кВ/см переместили заряд q = –20 нКл в направлении силовой линии поля на расстояние d = 10 см. Найти работу поля А, изменение потенциальной энергии поля ΔW_п и напряжение (разность потенциалов) U между начальной и конечной точками перемещения.

Задача № 9.
Между двумя горизонтальными плоскостями, заряженными разноименно и расположенными на расстоянии d = 5 мм друг от друга, находится в равновесии капелька масла массой 20 нг (нанограмм) (рис. 3-10). Найти число избыточных электронов N на этой капельке. Среда — воздух. Разность потенциалов между плоскостями U = 2 кВ.

Задача № 10.
На пластине М поддерживается потенциал φ₁ = +80 В, а на пластине N – φ₂ = –80 В (рис. 3-11, а). Расстояние между пластинами d = 10 см. На расстоянии d₁ = 4 см от пластины М помещают заземленную пластину Р (рис. 3-11, б). Найти изменение напряженности ΔЕ₁ поля на участке МР и изменение напряженности поля ΔЕ₂ на участке PN при этом. Построить графики зависимостей напряженностей Е = Е(х) и потенциала φ = φ(х) от расстояния между точками поля и пластинами.

Это конспект по теме «Потенциал. Разность потенциалов. ЗАДАЧИ с решениями». Выберите дальнейшие действия:

Вернуться к списку конспектов по Физике.
Проверить свои знания по Физике.

Потенциал системы точечных зарядов

Поскольку электрическое поле потенциально, и в нём действует принцип суперпозиции, это позволяет легко находить потенциал системы зарядов. Он равен алгебраической сумме элементарных зарядов:

$$\varphi_{общ} =\varphi_1+\varphi_2+…+\varphi_n$$

Эта же формула используется в том случае, если заряд распределен по телу неравномерно. Тело разбивается на множество элементарных областей, в каждой из которых заряд можно считать точечным. После этого потенциал всех областей суммируется.

Рис. 3. Потенциал системы зарядов.

Что мы узнали

Электростатический потенциал — это скалярная энергетическая характеристика электростатического поля. Она равна работе, которую надо совершить для того, чтобы удалить пробный единичный заряд из поля в бесконечность. Поскольку электрическое поле потенциально, и в нём работает принцип суперпозиции, потенциал системы точечных зарядов равен сумме потенциалов каждого заряда.

/10

Вопрос 1 из 10

Потенциал электрического поля. Разность потенциалов

Потенциал – скалярная физическая величина, равная отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда.

Обозначение – $ \varphi $, единица измерения в СИ – вольт (В).

Потенциал $ \varphi $ является энергетической характеристикой электростатического поля.

Разность потенциалов численно равна работе, которую совершает электрическая сила при перемещении единичного положительного заряда между двумя точками поля:

Обозначение – $ \Delta\varphi $, единица измерения в СИ – вольт (В).

Иногда разность потенциалов обозначают буквой $ U $ и называют напряжением.

Важно!
Разность потенциалов $ \Delta\varphi=\varphi_1-\varphi_2 $, а не изменение потенциала $ \Delta\varphi=\varphi_2-\varphi_1 $. Тогда работа электростатического поля равна:

Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле. В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки

В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность

В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Потенциал поля точечного заряда $ q $ в точке, удаленной от него на расстояние $ r $, вычисляется по формуле:

Для наглядного представления электрического поля используют эквипотенциальные поверхности.

Важно!
Внутри проводящего шара потенциал всех точек внутри шара равен потенциалу поверхности шара и вычисляется по формуле потенциала точечного заряда ($ r =R $, где $ R $ – радиус шара). Напряженность поля внутри шара равна нулю

Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение.

Свойства эквипотенциальных поверхностей

Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону убывания потенциала.
Работа по перемещению заряда по эквипотенциальной поверхности равна нулю.

В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Для точечного заряда эквипотенциальные поверхности представляют собой концентрические окружности.

Разность потенциалов и напряженность связаны формулой:

Из принципа суперпозиции полей следует принцип суперпозиции потенциалов:

Потенциал результирующего поля равен сумме потенциалов полей отдельных зарядов.

Важно!
Потенциалы складываются алгебраически, а напряженности – по правилу сложения векторов. Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил.

Алгоритм решения таких задач:

установить характер и особенности электростатических взаимодействий объектов системы;
ввести характеристики (силовые и энергетические) этих взаимодействий, сделать рисунок;
записать законы сохранения и движения для объектов;
выразить энергию электростатического взаимодействия через заряды, потенциалы, напряженности;
составить систему уравнений и решить ее относительно искомой величины;
проверить решение.

Разность потенциалов. Напряжение

Работа сил электростатического поля по перемещению заряда q из точки 1 в точку 2 поля

$~A_{12} = W_{1} — W_{2} .$

Выразим потенциальную энергию через потенциалы поля в соответствующих точках:

$~W_{1} = q_0 \cdot \varphi_1 , W_{2} = q_0 \cdot \varphi_2 .$

Тогда

$~A_{12} = q_0 \cdot (\varphi_1 — \varphi_2) .$

Таким образом, работа определяется произведением заряда на разность потенциалов начальной и конечной точек.

Из этой формулы разность потенциалов

$~\varphi_1 — \varphi_2 = \dfrac{A_{12}}{q_0} .$

Разность потенциалов — это скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между данными точками поля к этому заряду.

В СИ единицей разности потенциалов является вольт (В).

1 В — разность потенциалов между двумя такими точками электростатического поля, при перемещении между которыми заряда в 1 Кл силами поля совершается работа в 1 Дж.

Разность потенциалов в отличие от потенциала не зависит от выбора нулевой точки. Разность потенциалов φ₁ — φ₂ часто называют электрическим напряжением между данными точками поля и обозначают U:

$~U = \varphi_1 — \varphi_2 .$

Напряжение между двумя точками поля определяется работой сил этого поля по перемещению заряда в 1 Кл из одной точки в другую.

Работу сил электрического поля иногда выражают не в джоулях, а в электронвольтах.

1 эВ равен работе, совершаемой силами поля при перемещении электрона (е = 1,6·10-19 Кл) между двумя точками, напряжение между которыми равно 1 В.

1 эВ = 1,6·10-19 Кл·1 В = 1,6·10-19 Дж.

1 МэВ = 106 эВ = 1,6·10-13 Дж.

Работа электростатического поля. Потенциал. Эквипотенциальные поверхности

Подробности: Обновлено 14.08.2018 00:14; Просмотров: 695

Электростатическое поле — это электрическое поле неподвижного заряда.
Сила F эл, действующая на заряд, перемещает его, совершая раборту.
В однородном электрическом поле Fэл = qE — постоянная величина

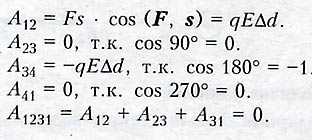
Работа поля (электрической силы) не зависит от формы траектории и на замкнутой траектории равна нулю.

ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ

Электростатическая энергия — потенциальная энергия системы заряженных тел (т.к. они взаимодействуют и способны совершить работу).

Так как работа поля не зависит от формы траектории, то одновременно

Сравнивая формулы работы, получим потенциальную энергию заряда в однородном электростатическом поле

Если поле совершает положительную работу ( вдоль силовых линий ), то потенциальная энергия заряженного тела уменьшается (но согласно закону сохранения энергии увеличивается кинетическая энергия ) и наоборот.

ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ

-энергитическая характеристика электрического поля.
— равен отношению потенциальной энергии заряда в поле к этому заряду.
— скалярная величина, определяющая потенциальную энергию заряда в любой точке электрического поля.

Величина потенциала считается относительно выбранного нулевого уровня.

РАЗНОСТЬ ПОТЕНЦИАЛОВ ( или иначе НАПРЯЖЕНИЕ )

— это разность потенциалов в начальной и конечной точках траектории заряда.

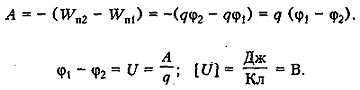
Напряжение между двумя точками ( U ) равно разности потенциалов этих точек и равно работе поля по перемещению единичного заряда.

СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ПОЛЯ И РАЗНОСТЬЮ ПОТЕНЦИАЛОВ

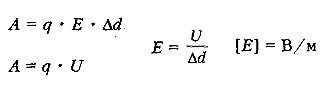
Чем меньше меняется потенциал на отрезке пути, тем меньше напряженность поля.
Напряженность электрического поля направлена в сторону уменьшения потенциала.

ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ

— поверхности, все точки которых имеют одинаковый потенциал

для однородного поля — это плоскость

для поля точечного заряда — это концентрические сферы

Эквипотенциальная поверхность имеется у любого проводника в электростатическом поле, т.к. силовые линии перпендикулярны поверхности проводника.
Все точки внутри проводника имеют одинаковый потенциал ( =0).
Напряженность внутри проводника = 0, значит и разность потенциалов внутри = 0.

Следующая страница «Электроемкость. Конденсаторы. Энергия заряженного конденсатора»

Назад в раздел «10-11 класс»

Электростатика и законы постоянного тока — Класс!ная физика

Электрический заряд. Электризация. Закон сохранения электрического заряда. Закон Кулона. Единица электрического заряда —
Близкодействие и дальнодействие. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции полей. Силовые линии электрического поля —
Проводники и диэлектрики в электростатическом поле. Поляризация диэлектриков —
Потенциальная энергия тела в электростатическом поле. Потенциал электростатического поля и разность потенциалов. Связь между напряженностью электростатического поля и разхностью потенциалов —
Электроемкость. Конденсаторы. Энергия заряженного конденсатора —
Электрический ток. Сила тока. Условия, необходимые для существования электрического тока. Закон Ома для участка цепи. Сопротивление —
Работа и мощность тока

Понятие разности потенциалов, формула нахождения

Подставим выражение для потенциала в точке в формулу для работы:

Физическую величину, смысл которой заключается в разнице между потенциалами в начальной и конечной точках траектории, называют разностью потенциалов или напряжением (U).

В самом простом случае, когда на рассматриваемую цепь или участок цепи действует только электростатическое поле, напряжение можно считать равным разности потенциалов. В иных случаях напряжение в проводнике определяют как сумму разности потенциалов и работу внешних сил (ЭДС), возникающих, например, в результате закона электромагнитной индукции. Тогда напряжение:

Чтобы понять связь между напряжением и напряженностью, рассмотрим простой конденсатор в виде двух пластин с постоянной емкостью.

Между положительно и отрицательно заряженными пластинами образуется электростатическое поле напряженностью \overrightarrow Е. Линии напряженности между обкладками параллельны, а модуль напряженности одинаков.

Напряжение и напряженность связаны формулой:

Разместим протяженный проводник в электростатическом поле. Будем считать, что линии напряженности расположены горизонтально.

Пусть проводник будет двигаться перпендикулярно линиям напряженности. В этом случае работа по перемещению заряда не совершается, так как косинус угла между векторами силы и скорости движения равен нулю. То есть все точки на поверхности проводника имеют один и тот же потенциал.

Закон Кулона. Принцип суперпозиции

Взаимодействие неподвижных электрических зарядов изучает раздел физики названный электростатикой, в основе которой фактически лежит закон Кулона, который был выведен на основе многочисленных опытов. Данный закон, также как и единица электрического заряда были названы в честь французского физика Шарля Кулона.

Кулон проводя свои опыты установил, что сила взаимодействия между двумя небольшими электрическим зарядами подчиняется следующим правилам:

сила пропорциональна величине каждого заряда;
сила обратно пропорциональна квадрату расстояний между ними;
направление действия силы направленно вдоль прямой соединяющей заряды;
сила представляет собой притяжение, если тела заряжены противоположно, и отталкивание в случае одноимённых зарядов.

Таким образом, закон Кулона выражается следующей формулой

где q1, q2 – величина электрических зарядов,

r – расстояние между двумя зарядами,

k – коэффициент пропорциональности, равный k = 1/(4πε0) = 9 * 109 Кл2/(Н*м2), где ε0 – электрическая постоянная, ε0 = 8,85 * 10-12 Кл2/(Н*м2).

Замечу, что ранее электрическая постоянная ε0 называлась диэлектрической постоянной или диэлектрической проницаемостью вакуума.

Рисунок иллюстрирующий закон Кулона.

Закон Кулона проявляется, нет только при взаимодействии двух зарядов, но и что чаще встречается системы из нескольких зарядов. В этом случае закон Кулона дополняется ещё одним существенным фактором, который называется «принципом наложения» или принципом суперпозиции.

В основе принципа суперпозиции лежит два правила:

воздействие на заряженную частицу нескольких сил есть векторная сумма воздействий этих сил;
любое сложное движение состоит из нескольких простых движений.

Принцип суперпозиции, на мой взгляд, проще всего изобразить графически

Изображение, поясняющее принцип суперпозиции.

На рисунке показаны три заряда: -q1, +q2, +q3. Для того чтобы вычислить силу Fобщ, которая действует на заряд -q1, необходимо вычислить по закону Кулона силы взаимодействия F1 и F2 между -q1, +q2 и -q1, +q3. Затем получившиеся силы сложить по правилу сложения векторов. В данном случае Fобщ вычисляется как диагональ параллелограмма по следующему выражению

где α – угол между векторами F1 и F2.

Диэлектрики в электрическом поле

Диэлектриками называют вещества, не проводящие электрический ток. Диэлектриками являются стекло, фарфор, резина, дистиллированная вода, газы.

В диэлектриках нет свободных зарядов, все заряды связаны. В молекуле диэлектрика суммарный отрицательный заряд электронов равен положительному заряду ядра. Различают полярные и неполярные диэлектрики.

В молекулах полярных диэлектриков ядра и электроны расположены так, что центры масс положительных и отрицательных зарядов не совпадают и находятся на некотором расстоянии друг от друга. То есть молекулы представляют собой диполи независимо от наличия внешнего электрического поля. В отсутствие внешнего электрического поля из-за теплового движения молекул диполи расположены хаотично, поэтому суммарная напряженность поля всех диполей диэлектрика равна нулю.

Если в отсутствие внешнего электрического поля центры масс положительных и отрицательных зарядов в молекуле диэлектрика совпадают, то он называется неполярным. Пример такого диэлектрика – молекула водорода. Если такой диэлектрик поместить во внешнее электрическое поле, то направления векторов сил, действующих на положительные и отрицательные заряды, будут противоположными. В результате молекула деформируется и превращается в диполь. При внесении диэлектрика в электрическое поле происходит его поляризация.

Поляризация диэлектрика – процесс смещения в противоположные стороны разноименных связанных зарядов, входящих в состав атомов и молекул вещества в электрическом поле.

Если диэлектрик неполярный, то в его молекулах происходит смещение положительных и отрицательных зарядов. На поверхности диэлектрика появятся поверхностные связанные заряды. Связанными эти заряды называют потому, что они не могут свободно перемещаться отдельно друг от друга.

Внутри диэлектрика суммарный заряд равен нулю, а на поверхностях заряды не скомпенсированы и создают внутри диэлектрика поле, вектор напряженности которого направлен противоположно вектору напряженности внешнего поля. Это значит, что внутри диэлектрика поле имеет меньшую напряженность, чем в вакууме.

Физическая величина, равная отношению модуля напряженности электрического поля в вакууме к модулю напряженности электрического поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества:

В полярном диэлектрике во внешнем электрическом поле происходит поворот диполей, и они выстраиваются вдоль линий напряженности.

Если внесенный в электрическое поле диэлектрик разрезать, то его части будут электрически нейтральны.