Задачи на работу электрического поля и потенциал с решениями

Проводники в электрическом поле

Проводниками называют вещества, в которых может происходить упорядоченное перемещение электрических зарядов, т. е. протекать электрический ток.

Проводниками являются металлы, водные растворы солей, кислот, ионизованные газы. В проводниках есть свободные электрические заряды. В металлах валентные электроны взаимодействующих друг с другом атомов становятся свободными.

Если металлический проводник поместить в электрическое поле, то под его действием свободные электроны проводника начнут перемещаться в направлении, противоположном направлению напряженности поля. В результате на одной поверхности проводника появится избыточный отрицательный заряд, а на противоположной – избыточный положительный заряд.

Эти заряды создают внутри проводника внутреннее электрическое поле, вектор напряженности которого направлен противоположно вектору напряженности внешнего поля. Под действием внешнего электростатического поля электроны проводимости в металлическом проводнике перераспределяются так, что напряженность результирующего поля в любой точке внутри проводника равна нулю. Электрические заряды расположены на поверхности проводника.

Важно!Если внутри проводника есть полость, то напряженность в ней будет равна нулю независимо от того, какое поле имеется вне проводника и как заряжен проводник. Внутренняя полость в проводнике экранирована (защищена) от внешних электростатических полей

На этом основана электростатическая защита.

Явление перераспределения зарядов во внешнем электростатическом поле называется электростатической индукцией.

Заряды, разделенные электростатическим полем, взаимно компенсируют друг друга, если проводник удалить из поля. Если такой проводник разрезать, не вынося из поля, то его части будут иметь заряды разных знаков.

Важно!
Во всех точках поверхности проводника вектор напряженности направлен перпендикулярно к его поверхности. Поверхность проводника является эквипотенциальной (потенциалы всех точек поверхности проводника равны)

Задача по физке — 12119

ГЛАВНАЯ » РЕШЕБНИК

2019-12-17   Внутри диэлектрического шара радиуса $R_{0}$, равномерно заряженного с объемной плотностью $\rho$ находится заземленная металлическая сфера радиуса $r$ (рис.). Найдите зависимость потенциала электростатического поля этой системы от расстояния до центра сферы.

Решение:Согласно принципу суперпозиции, напряженность электростатического поля системы равна сумме напряженностей полей, создаваемых зарядами шара и сферы. Аналогично и потенциал поля в каждой точке равен сумме потенциалов полей зарядов сферы и шара.
Обозначим заряд заземленной металлической сферы через $q$ (позже найдем его значение); очевидно, что $q Потенциал $\phi$ этого поля вне сферы меняется по закону $\phi = \frac{q}{4 \pi \epsilon_{0}R }$, а внутри сферы — равен потенциалу поверхности сферы: $\phi = \frac{q}{4 \pi \epsilon_{0}r }$. На рисунке синей линией изображен график зависимости $\phi$ от $R$.
Равномерно заряженный шар вне себя (при $R \geq R_{0}$) создает поле такое же, как точечный заряд, равный заряду шара $Q = \frac{4}{3} \pi \rho R_{0}^{3}$, находящийся в его центре: $E = \frac{Q}{4 \pi \epsilon_{0}R^{2} } = \frac{ \rho R_{0}^{3} }{3 \epsilon_{0}R^{2} }$. Внутри шара на расстоянии $R
Потенциал поля заряженного шара вне шара равен потенциалу поля точечного заряда $Q$, помещенного в центр шара: $\phi = \frac{Q}{4 \pi \epsilon_{0}R } = \frac{ \rho R_{0}^{2} }{3 \epsilon_{0}R }$.
На поверхности шара $\phi = \frac{ \rho R_{0}^{2} }{3 \epsilon_{0} }$, а по мере приближения к центру шара потенциал растет: добавляется работа, совершаемая электрическим полем по перенесению единичного заряда из рассматриваемой точки внутри шара на его поверхность. Эта работа равна средней напряженности поля на рассматриваемом участке, умноженной на перемещение единичного заряда. Поскольку внутри шара напряженность меняется линейно.
$E_{ср} = \frac{E_{R} + E_{R_{0} } }{2} = \frac{ \rho (R + R_{0} ) }{6 \epsilon_{0} }$.
Тогда потенциал поля внутри шара равен
$\phi = \frac{ \rho R_{0}^{2} }{3 \epsilon_{0} } + E_{ср}(R_{0} — R) = \frac{ \rho R_{0}^{2} }{3 \epsilon_{0} } + \frac{ \rho (R_{0}^{2} — R^{2} ) }{6 \epsilon_{0} } = \frac{ \rho (3R_{0}^{2} — R^{2} ) }{6 \epsilon_{0} }$.
Соответствующий график показан на рисунке черной линией.
Для того чтобы построить график зависимости потенциала $\phi$ поля системы от $R$, надо сложить графики, построенные отдельно для полей сферы и шара. На рисунке результирующий график показан красной линией.
Осталось найти величину $q$ заряда на сфере. Так как сфера заземлена, ее потенциал равен нулю. Это означает, что на поверхности сферы, при $R = r$, потенциал поля системы равен нулю:
$\frac{q}{4 \pi \epsilon_{0}r } + \frac{ \rho R_{0}^{2} }{3 \epsilon_{0} } + \frac{ \rho (R_{0}^{2} — r^{2} ) }{6 \epsilon_{0} } = 0$.
Отсюда
$q = — \frac{2}{3} \pi \rho r (3R_{0}^{2} — r^{2} )$.

Соединение с Землей.

Чтобы разрядить какое-либо
тело, мы соединяем его с заземленным предметом, например, с водопроводным
краном, или просто касаемся рукой. При этом мы говорим, что «заряды ушли
с проводника в землю».

Более точно явление заключается
в следующем. Действие электрического поля мы наблюдаем только тогда, когда
есть разность потенциалов между рассматриваемым телом и окружающими предметами.
Если же соединить это тело с землей, то разность потенциалов между этим
телом и окружающими заземленными предметами исчезает, и, следовательно,
исчезает электрическое поле.

Следует заметить, что соединение
именно с землей не играет принципиальной роли. Наблюдалось бы то же самое, если
бы вместо заземленных предметов, например, стен комнаты, был замкнутый проводник
изолированный от земли.

Циркуляция и ротор(математическое отступление).

Как мы видели в пункте 1,
работа электростатического поля оказалась равной криволинейному интегралу, вычисленному
вдоль траектории, по которой движется заряд.

Вообще в математике криволинейный интеграл от любой векторной функции
по кривой (контуру) L означает следующее.
Разделим всю кривую на очень малые элементы
и получим векторы с направлениями,
определяемыми выбором движения, модули которых равны длинам этих участков; для
каждого вычислим скалярное произведение ;
просуммируем
полученные результаты; переходя к пределу бесконечно малых элементов кривой,
получим криволинейный интеграл (или интеграл по контуру).

Пусть теперь в области пространства, в которой определено векторное поле расположена
произвольная замкнутая кривая L (рис.6.3).

def: Циркуляцией вектора по произвольному замкнутому контуру L называется криволинейный интеграл Г , (6.7) где — единичный вектор, касательный к контуру L, указывающий направление обхода этого контура.

Фактически интегрируется только касательная составляющая
векторного поля А_l, поэтому помимо (6.7) для обозначения циркуляции
используют ещё следующие эквивалентные формулы:

.

Будем, кроме того, считать, что на контуре выбрано положительное
направление обхода, то есть направление, при движении, вдоль которого область,
ограниченная контуром, остаётся всегда слева (более точно см. ниже).

Вновь вспомним о гидродинамике. Если мы рассмотрим векторное
поле скоростей текущей
жидкости, и поместим в произвольную точку этой жидкости небольшую турбинку (колёсико
с лопастями) то в зависимости от своей ориентации, турбинка будет вращаться
с большей или меньшей скоростью. Если вычислить циркуляцию вектора скорости
вдоль контура, совпадающего с ободом турбинки, а затем разделить на длину этого
обода, то мы получим (в соответствие с теоремой о среднем) некоторое среднее
значение проекции скорости частиц жидкости на касательную к контуру v_l. Но именно
с такой линейной скоростью и будут вращаться лопасти турбинки. Таким образом,
чем больше циркуляция вектора скорости, тем с большей скоростью будет вращаться
турбинка, помещённая в данную точку жидкости, а это в свою очередь означает,
большую завихрённость жидкости в рассматриваемой точке. (Характерный пример
— вода, вытекающая из ванны.)

Следует отметить, однако, что характеризовать
завихрённость поля непосредственно циркуляцией Г нельзя, поскольку поле может
быть очень неоднородным, и степень его завихрённости будет изменяться от точки
к точке. Желая же определить такую «локальную» завихрённость, мы должны будем
уменьшать размеры контура L, стягивая его в точку. При этом,
очевидно, циркуляция будет стремиться к 0. В связи с этим, для характеристики
степени завихрённости поля вводят понятие плотности циркуляции, определяя её
как предел, к которому стремится отношение циркуляции вектора
по контуру L, к площади
DS,
ограниченной этим контуром, когда данный контур стягивается
к рассматриваемой точке пространства. (При этом, соответственно, DS0):

.

Вычисляя этот предел, мы будем иметь уже некоторое конечное,
отличное от нуля число. Однако, это значение будет зависеть от ориентации контура L в поле.
Например, как уже говорилось ранее,
от ориентации турбинки в жидкости. Изменяя ориентацию турбинки, мы можем получить
максимальное и минимальное значения Г (соответствующие двум противоположным
ориентациям турбинки, при этом одно из них будет положительным, а другое отрицательным),
а также при некоторой ориентации турбинка вообще перестанет вращаться, что соответствует
Г=0. Данные обстоятельства показывают, что всё многообразие значений плотности
циркуляции векторного поля может быть, вообще говоря, представлено в виде проекции
некоторого вектора, на нормаль к площадке контура L. При этом данный вектор
по абсолютной величине будет равен максимальному значению плотности циркуляции
вектора в рассматриваемой
точке пространства, и направлен в сторону, соответствующую направлению нормали
к контуру L, при которой плотность циркуляции принимает это максимальное значение.

Данный вектор называется ротором или вихрем векторного поля
(от французского
(или английского) слова rotation — вращение, или лат. roto- вращаюсь) и проекция этого
вектора на любое направление в каждой точке пространства определяется
выражением:

    (6.10)

Здесь — нормаль
к площадке DS, согласованная с направлением обхода контура L
правилом правого винта (буравчика) — рис.6.4.

Поле точечного заряда и заряженного шара. Принцип суперпозиции полей

Подробности

Обновлено 13.08.2018 18:45

Просмотров: 745

«Физика — 10 класс»

Что показывают силовые линии?
Для чего они используются?

Напряжённость поля точечного заряда.

Найдём напряжённость электрического поля, создаваемого точечным зарядом q. По закону Кулона этот заряд будет действовать на положительный заряд q с силой

Модуль напряжённости поля точечного заряда q на расстоянии г от него равен:

Вектор напряжённости в любой точке электрического поля направлен вдоль прямой, соединяющей эту точку и заряд (рис. 14.14), и совпадает с силой, действующей на точечный положительный заряд, помещённый в данную точку.

Силовые линии электрического поля точечного заряда, как следует из соображений симметрии, направлены вдоль радиальных линий (рис. 14.15, а).

Поле заряженного шара.

Рассмотрим теперь вопрос об электрическом поле заряженного проводящего шара радиусом R. Заряд q равномерно распределён по поверхности шара. Силовые линии электрического поля, также из соображений симметрии, направлены вдоль продолжений радиусов шара (рис. 14.15, б).

Распределение в пространстве силовых линий электрического поля шара с зарядом q на расстояниях r ≥ R от центра шара аналогично распределению силовых линий поля точечного заряда q (см. рис. 14.15, а). Следовательно, на расстоянии r ≥ R от центра шара напряжённость поля определяется той же формулой (14.9), что и напряжённость поля точечного заряда, помещённого в центре сферы:

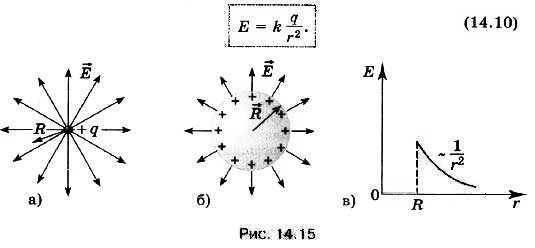
Внутри проводящего шара (r < R) напряженность поля равна нулю.

Принцип суперпозиции полей.

Если на тело действует несколько сил, то согласно законам механики результирующая сила равна геометрической сумме этих сил:

= ₁ + ₂ + … .

На электрические заряды действуют силы со стороны электрического поля. Если при наложении полей от нескольких зарядов эти поля не оказывают никакого влияния друг на друга, то результирующая сила со стороны всех полей должна быть равна геометрической сумме сил со стороны каждого поля. Опыт показывает, что именно так и происходит на самом деле. Это означает, что напряжённости полей складываются геометрически.

В этом состоит принцип суперпозиции полей.

Если в данной точке пространства различные заряженные частицы создают электрические поля, напряжённости которых ₁, ₂, ₃ и т. д., то результирующая напряжённость поля в этой точке равна сумме напряжённостей этих полей:

= ₁ + ₂ + ₃ + … .         (14.11)

Напряжённость поля, создаваемого отдельным зарядом, определяется так, как будто других зарядов, создающих поле, не существует.

Согласно принципу суперпозиции полей для нахождения напряжённости поля системы заряженных частиц в любой точке достаточно знать выражение (14.9) для напряжённости поля точечного заряда.

Для определения направления векторов напряжённостей полей отдельных зарядов мысленно помещаем в выбранную точку положительный заряд.

На рисунке 14.16 показано, как определяется напряжённость поля в точке А, созданного двумя точечными зарядами q₁ и q₂.

Следующая страница «Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей»»

Назад в раздел «Физика — 10 класс, учебник Мякишев, Буховцев, Сотский»

Электростатика — Физика, учебник для 10 класса — Класс!ная физика

Что такое электродинамика —
Электрический заряд и элементарные частицы. Закон сохранения заряд —
Закон Кулона. Единица электрического заряда —
Примеры решения задач по теме «Закон Кулона» —
Близкодействие и действие на расстоянии —
Электрическое поле —
Напряжённость электрического поля. Силовые линии —
Поле точечного заряда и заряженного шара. Принцип суперпозиции полей —
Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» —
Проводники в электростатическом поле —
Диэлектрики в электростатическом поле —
Потенциальная энергия заряженного тела в однородном электростатическом поле —
Потенциал электростатического поля и разность потенциалов —
Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности —
Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» —
Электроёмкость. Единицы электроёмкости. Конденсатор —
Энергия заряженного конденсатора. Применение конденсаторов —
Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»

Решение задач на разность потенциалов и работу поля: примеры

Задача №1 на потенциальную энергию системы зарядов

Условие

Два точечных заряда величиной 100 нКл и 10 нКл находятся на расстоянии r=10 см друг от друга. Вычислить потенциальную энергию системы этих зарядов.

Решение

Потенциал поля точечного заряда равен:

Так что, потенциальная энергия зарядов будет равна:

Подставим значения из условия и найдем:

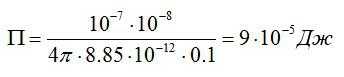Ответ: П=9*10^-5 Дж.

Задача №2 на определение потенциала заряженных шаров

Условие

Шар радиусом R1=6 см заряжен до потенциала 300 В , а шар радиусом R2=4 см – до потенциала 500 В. Найдите потенциал шаров после того, как их соединили металлическим проводом, емкостью которого можно пренебречь.

Решение

Потенциал шара равен:

Суммарный заряд двух шаров будет равен:

После соединения шаров заряд каждого будет равен:

Тогда суммарный потенциал шаров вычислится по формуле:

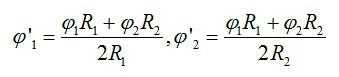
Подставим значения и найдем:  

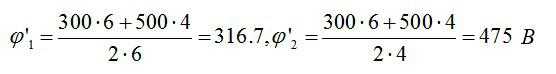
Ответ: 317 В; 475 В.

Задача №3 на разность потенциалов и работу по перемещению заряда

Условие

Заряд переместился между двумя точками с разностью потенциалов 1 кВ, при этом поле совершило работу, равную 40 мкДж. Найдите величину заряда.

Решение

По определению, разность потенциалов равна работе по перемещению заряда, деленной на величину этого заряда:

Отсюда можно выразить заряд и вычислить ответ:

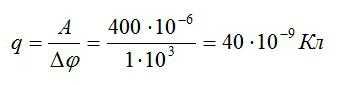
Ответ: 40 нКл.

Задача №4 на работу электрического поля по перемещению заряда

Условие

Два точечных заряда q1=6 мкКл  и  q2=2 мкКл, находятся на расстоянии а=60 см друг от друга. Какую работу необходимо свершить внешним силам, чтобы уменьшить расстояние между зарядами вдвое?

Решение

Находясь на расстоянии a, точечные заряды обладали потенциальной энергией:

На вдвое меньшем расстоянии энергия зарядов равна:

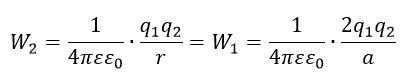
Работа, затраченная на сближение зарядов:

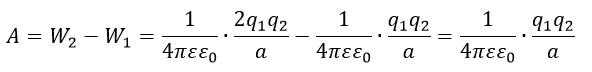
Подставляем числовые данные и вычисляем:

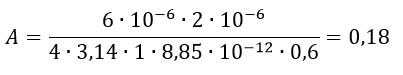
Ответ: A=0,18 Дж.

Задача №5 на движение заряженной частицы в поле

Условие

Электрон влетает в плоский воздушный конденсатор параллельно его пластинам со скоростью V=5·107 м/с. Расстояние между пластинами d=2 см, разность потенциалов U=500 В. Найти отклонение электрона, вызванное полем конденсатора, если длина его пластины l=5 см.

Решение

При движении в электрическом поле конденсатора на электрон действует сила:

Ускорение электрона, по 2 закону Ньютона, определяется формулой:

Время движения электрона в конденсаторе вычислим, зная длину пластины и скорость частицы:

Отклонение электрона будет равно:

Найдем:

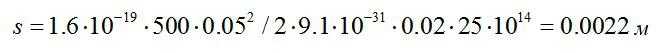
Ответ: 2.2 мм

Определение

Электрическое поле неразрывно связано с магнитным полем, и возникает в результате его изменения. Эти два вида материи являются компонентами электромагнитных полей, заполняющих пространство вокруг заряженных частиц или заряженных тел.

Таким образом, данный термин означает особый вид материи, обладающий собственной энергией, являющийся составным компонентом векторного электромагнитного поля. У электрического поля нет границ, однако его силовое воздействие стремится к нулю, при удалении от источника – заряженного тела или точечных зарядов .

Важным свойством полевой формы материи является способность электрического поля поддерживать упорядоченное перемещение носителей зарядов.

Рис. 1. Определение понятия «электрическое поле»

Энергия электрического поля подчиняется действию закона сохранения. Её можно преобразовать в другие виды или направить на выполнение работы.

Силовой характеристикой полей выступает их напряжённость – векторная величина, численное значение которой определяется как отношение силы, действующей на пробный положительный заряд, к величине этого заряда.

Характерные физические свойства:

• реагирует на присутствие заряженных частиц;
• взаимодействует с магнитными полями;
• является движущей силой по перемещению зарядов – как положительных ионов, таки отрицательных зарядов в металлических проводниках;
• поддаётся определению только по результатам наблюдения за проявлением действия.

Оно всегда окружает неподвижные статичные (не меняющиеся со временем) заряды, поэтому получило название – электростатическое. Опыты подтверждают, что в  электростатическом поле действуют такие же силы, как и в электрическом.

Электростатическое взаимодействие поля на заряженные тела можно наблюдать при поднесении наэлектризованной эбонитовой палочки к мелким предметам. В зависимости от полярности наэлектризованных частиц, они будут либо притягиваться, либо отталкиваться от палочки.

Сильные электростатические поля образуются вблизи мощных электрических разрядов. На поверхности проводника, оказавшегося в зоне действия разряда, происходит перераспределение зарядов.

Вследствие распределения зарядов проводник становится заряженным, что является признаком влияния электрического поля.

Вопросы на тему «Работа электрического поля и разность потенциалов»

Вопрос 1. Что такое потенциал электрического поля?

Ответ. Потенциал – скалярная физическая величина, являющаяся энергетической характеристикой электростатического поля.

Потенциал поля равен отношению потенциальной энергии поля (или работы по перемещению заряда из данной точки на нулевой уровень потенциальной энергии) к величине заряда.

Для потенциала применим принцип суперпозиции.

Вопрос 2. Что такое разность потенциалов?

Ответ. Разность потенциалов – это работа по перемещению заряда из одной точки в другую. Разность потенциалов еще называют напряжением, обозначая его как разность потенциалов в начальной и конечной точках траектории заряда.

Вопрос 3. Что происходит с зарядом, когда он попадает в электрическое поле?

Ответ. На заряд со стороны поля действует сила, способная перемещать заряд в поле и совершать работу.

Вопрос 4. Какую природу имеет сила, действующая на заряд? Зависит ли величина работы от траектории заряда в поле?

Ответ. Сила, действующая со стороны поля на заряд, является проявлением электромагнитного взаимодействия. Величина работы поля не зависит от траектории заряда, так как это работа потенциальных (консервативных) сил.

Для наилучшего понимания сути задач на потенциал и работу поля, можно провести параллель между работой по перемещению заряда, потенциальной энергией в механике и работой силы тяжести.

Вопрос 5. Что такое эквипотенциальная поверхность?

Ответ. Это поверхность, во всех точках которой потенциал электрического поля имеет одинаковое значения.

Формула Стокса(математическое отступление).

В математике доказывается следующее соотношение, называемое
формулой (теоремой)
,
связывающее циркуляцию вектора по контуру
L с интегралом от ротора этого вектора по поверхности S,
охватываемой данным контуром (рис.6.4а).

Lex: Циркуляция векторного поля вдоль некоторого замкнутого контура L равна потоку ротора этого векторного поля через поверхность S, опирающуюся (натянутую) на этот контур. ,   (6.14)

При этом направление нормали к поверхности
S также должно быть согласовано с направлением обхода контура
L по правилу правого винта. Следует отметить, что данное
согласование в математике определяется следующим образом:

Наблюдатель, обходящий контур L и направленный по нормали
, должен
иметь поверхность S слева. При этом обход контура L
совершается в положительном направлении. (Или: нормаль в каждой точке
поверхности нужно направить в ту сторону, откуда обход контура кажется совершающимся
против часовой стрелки.)

Работа поля точечного заряда.

Более правильно название данного раздела должно звучать
так: «Работа электростатического поля, созданного точечным зарядом Q, по перемещению точечного заряда
q из точки 1 в точку 2». Но мы с вами и так понимаем, о чем речь.

Начало координат выбрано в точке, в которой находится заряд Q. Из рис.6.2 видно, что
. Учитывая, что

,

,

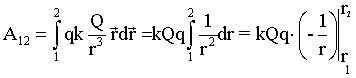   (6.3)

Можно сделать вывод, что работа электростатического
поля, созданного точечным зарядом, а также любого другого центрально-симметричного
поля, не зависит от формы пути, а определяется только начальным и конечным положением.

очевидно, что работа поля при перемещении заряда по замкнутому контуру равна 0.

   (6.4)

Дивергенция и ротор (Как вы это поняли).

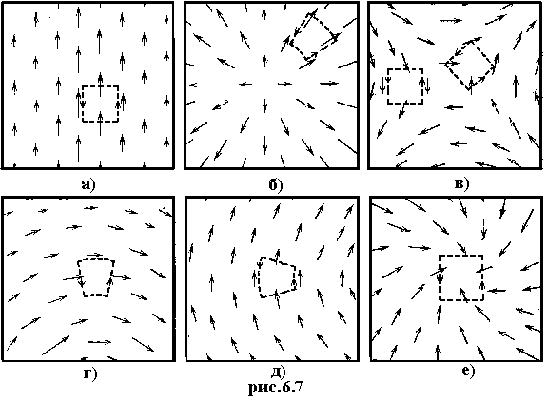
На рис.6.7 представлены различные картины векторного поля. Попробуйте сказать,
где ротор и дивергенция равны 0, а где нет

При этом прежде всего нужно обратить
внимание на контуры интегрирования, заметив, что они выбраны так, чтобы вдоль
каждой из сторон, проекция векторов поля имела одно и тоже значение (причём
для двух сторон в случаях а, б, г, д она равна 0)

Ответ:

a) вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. ротор не равен нулю. Сравните с рекой.	б) Явно виден источник поля. Дивергенция не равна нулю. Поле центрально — симметричное. Поэтому ротор равен 0.	в) вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. Проекции векторов поля на противоположные стороны контура разных знаков, но одинаковы по абсолютной величине, и поэтому при сложении линейных интегралов они уничтожают друг друга. Поэтому ротор равен нулю.
г) вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. Вектор убывает по мере удаления от центра поля (за пределами рисунка) поэтому ротор может быть равен 0.	д) вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. Вектор не убывает, поэтому линейный интеграл по левой стороне контура не компенсируется таким же интегралом по правой. Поэтому ротор не равен нулю.	е) Явно виден сток поля. Поэтому дивергенция не равна 0. Так же и ротор не равен нулю, поскольку циркуляция вдоль указанного контура не равна 0, так как проекции векторов поля на все стороны контура одного знака (отрицательны) и при сложении (интегрировании) не компенсируют друг друга.

Подводя итог, ещё раз отметим, что ротор характеризует степень
завихрённости векторного поля, его «вращательную составляющую». При этом, однако,
нужно иметь в виду, что данная «вращательная компонента» поля может быть обусловлена
не только искривлением векторных линий (завихрённость «в чистом виде»), как
при вытекании воды из ванны, или в примере е), но и поперечной неоднородностью
поля, когда векторные линии — прямые, как в случае течения воды в реке (рис.6.5),
или в случае примера а).

Ротор в физике.

Понятно, что если циркуляция напряженности электростатического поля равна 0, то и

      (6.15)

Если поле имеет ротор, отличный от нуля, то оно имеет некоторую
завихренность, например, вода, вытекающая из ванны.

Проведем дальнейшие аналогии с гидродинамикой. На
реке скорость течения обычно у берегов меньше, чем на фарватере. Деревянная
щепка может служить “ротор-метром”. Она будет вращаться во всех точках,
кроме строго центральных. Поэтому ротор этого векторного поля скоростей
отличен от нуля.

Чтобы построить электрический “ ротор-метр” — по крайней
мере в воображении — следует положительные пробные заряды прикрепить к
какому-либо центру на изолирующих спицах. Если в поле эта система будет
вращаться, то ротор отличен от нуля. Понятно, что размеры нашего прибора
должны быть достаточно малы.